CM các bất phương trình sau luôn dương vs mọi x
1)2x2-2x+17>0
2)-x2+6x-18<0
3)|x-1|+|x|+2>1
Những câu hỏi liên quan
CMR: các bt sau luôn có gt dương vs mọi gt của biến
a, 9x2 - 6x + 2
b, x2 + x + 1
c, 2x2 + 2x + 1
CMR: bt sau luôn âm vs mọi gt của biến
-9x2 + 12x - 15
câu a: 9x^2-6x+2=(3x-1)^2+1>=1>0 mọi x
câu b:x^2+x+1=(x-1/2)^2+3/4>0 với mới x
Đúng 0
Bình luận (0)
Cho bất phương trình
2
−
x
2
+
2
x
+
1
+
2
x
2
−
2
x
≥
m
.
Tìm m để bất phương trình đúng với mọi
x
∈...
Đọc tiếp
Cho bất phương trình 2 − x 2 + 2 x + 1 + 2 x 2 − 2 x ≥ m . Tìm m để bất phương trình đúng với mọi x ∈ ℝ
A. m ≤ 3
B. m ≥ 3 2
C. m ≤ 2 2
D. m ≤ 3 2
Đáp án C
Đặt t = 2 x 2 − 2 x , t ∈ 0 ; + ∞ ⇒ B P T ⇔ 2 t + t ≥ m 1
Ta có t + 2 t ≥ 2 t . 2 t = 2 2 ⇒ 1 ⇔ m ≤ 2 2
Đúng 0
Bình luận (0)
Cho các phương trình có tham số m sau:
m
2
+
1
x
2
-
m
-
6
x
-
2
0
(1);
x
2
+
m
+
3
x
-
1
0
(2);
m
x
2
-...
Đọc tiếp
Cho các phương trình có tham số m sau:
m 2 + 1 x 2 - m - 6 x - 2 = 0 (1); x 2 + m + 3 x - 1 = 0 (2);
m x 2 - 2 x - m = 0 (3); 2 x 2 - 2 m x - 1 - m = 0 (4).
Phương trình nào có hai nghiệm phân biệt với mọi giá trị của m?
Chỉ ra khẳng định sai trong các khẳng định sau:
A. Phương trình (1)
B. Phương trình (2)
C. Phương trình (3)
D. Phương trình (4)
*Xét phương trình (m2 +1).x2 – (m- 6)x - 2= 0 có a= m2 + 1 >0 và c = -2 < 0 nên ac< 0 mọi m.
=> Phương trình (1) luôn có nghiệm mọi m.
* Phương trình x 2 + m + 3 x - 1 = 0 có ac= 1. (-1) < 0 nên phương trình này luôn có nghiệm mọi m.
* Xét (3) mx2 - 2x – m = 0 . Khi m= 0 thì (3) trở thành: - 2x = 0 đây là phương trình bậc nhất có nghiệm duy nhất là x = 0.
* Xét (4) có :
∆ = - 2 m 2 - 4 . 2 - 1 - m = 4 m 2 + 8 + 8 m = 4 m 2 + 8 m + 4 + 4 = 4 m + 1 2 + 4 > 0 ∀ m
Nên trình (4) luôn có 2 nghiệm phân biệt với mọi m.
Chọn C.
Đúng 0
Bình luận (0)
Hãy cho biết phương trình nào trong các phương trình sau đây là phương trình đường tròn:
2x2 + y2 – 8x + 2y – 1 = 0;
x2 + y2 + 2x – 4y – 4 = 0;
x2 + y2 – 2x – 6y + 20 = 0;
x2 + y2 + 6x + 2y + 10 = 0.
+ 2x2 + y2 – 8x + 2y – 1 = 0 không phải phương trình đường tròn vì hệ số của x2 khác hệ số của y2.
+ Phương trình x2 + y2 + 2x – 4y – 4 = 0 có :
a = –1; b = 2; c = –4 ⇒ a2 + b2 – c = 9 > 0
⇒ phương trình trên là phương trình đường tròn.
+ Phương trình x2 + y2 – 2x – 6y + 20 = 0 có :
a = 1; b = 3; c = 20 ⇒ a2 + b2 – c = –10 < 0
⇒ phương trình trên không là phương trình đường tròn.
+ Phương trình x2 + y2 + 6x + 2y + 10 = 0 có :
a = –3; b = –1; c = 10 ⇒ a2 + b2 – c = 0 = 0
⇒ phương trình trên không là phương trình đường tròn.
Đúng 0
Bình luận (0)
Giải các phương trình sau:
g/ x(x + 3)(x – 3) – (x + 2)(x2 – 2x + 4) = 0
h/ (3x – 1)(x2 + 2) = (3x – 1)(7x – 10)
i/ (x + 2)(3 – 4x) = x2 + 4x + 4
k/ x(2x – 7) – 4x + 14 = 0
m/ x2 + 6x – 16 = 0
n/ 2x2 + 5x – 3 = 0
\(m,x^2+6x-16=0\)
\(\Leftrightarrow x^2-2x+8x-16=0\)
\(\Leftrightarrow x\left(x-2\right)+8\left(x-2\right)=0\)
\(\Leftrightarrow\left(x+8\right)\left(x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+8=0\\x-2=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-8\\x=2\end{matrix}\right.\)
\(n,2x^2+5x-3=0\)
\(\Leftrightarrow2x^2-x+6x-3=0\)
\(\Leftrightarrow x\left(2x-1\right)+3\left(2x-1\right)=0\)
\(\Leftrightarrow\left(x+3\right)\left(2x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+3=0\\2x-1=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=\dfrac{1}{2}\end{matrix}\right.\)
Đúng 2
Bình luận (0)
\(k,x\left(2x-7\right)-4x+14=0\)
\(\Leftrightarrow2x^2-4x-7x+14=0\)
\(\Leftrightarrow2x\left(x-2\right)-7\left(x-2\right)=0\)
\(\Leftrightarrow\left(2x-7\right)\left(x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-7=0\\x-2=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{7}{2}\\x=2\end{matrix}\right.\)
Đúng 2
Bình luận (1)
Xem thêm câu trả lời
Giải bất phương trình sau:
x
2
-
x
-
2
x
2
-
x
-
1
≥
0
A. B. C. D.
Đọc tiếp
Giải bất phương trình sau:
x 2 - x - 2 x 2 - x - 1 ≥ 0
A.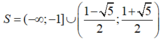 
B. 
C. 
D.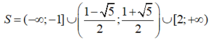 
Chọn D
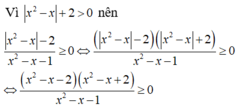
Bảng xét dấu
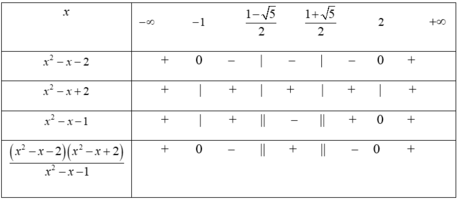
Dựa vào bảng xét dấu, ta có tập nghiệm của bất phương trình đã cho là
Đúng 0
Bình luận (0)
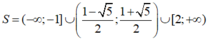
Cho bất phương trình (m-2)x^2 + 2(4-3m)x+10m-11 <=0 .Gọi S là tập hợp các số nguyên dương m để bất phương trình luôn đúng với mọi x<-4
Giúp vs ạBài 1 giải các bất phương trình saua.x2 - x - 6 0b.2x2 - 7x + 5 0c.3x2 - 9x + 6 ≥ 0d.2x2 - 5x + 3 0Bài 2 Giải phương trình sauA.√x2 + x + 5 √2x2 - 4x + 1B.√11x2 -14x - 12 √3x2 + 4x - 7
Đọc tiếp
Giúp vs ạ
Bài 1 giải các bất phương trình sau
a.x2 - x - 6 = 0
b.2x2 - 7x + 5 < 0
c.3x2 - 9x + 6 ≥ 0
d.2x2 - 5x + 3 < 0
Bài 2 Giải phương trình sau
A.√x2 + x + 5 = √2x2 - 4x + 1
B.√11x2 -14x - 12 = √3x2 + 4x - 7
Bài 2:
a: =>2x^2-4x+1=x^2+x+5
=>x^2-5x-4=0
=>\(x=\dfrac{5\pm\sqrt{41}}{2}\)
b: =>11x^2-14x-12=3x^2+4x-7
=>8x^2-18x-5=0
=>x=5/2 hoặc x=-1/4
Đúng 0
Bình luận (0)
Bài 1: Chứng minh các biểu thức sau luôn dương với mọi x:
a) 9x2 - 6x + 11
b) 3x2 - 12x + 81
c) 5x2 - 5x + 4
d) 2x2 - 2x + 9
a) \(9x^2-6x+11=\left(3x\right)^2-2.3x+1+10=\left(3x-1\right)^2+10>0\forall x\)
b) \(3x^2-12x+81=3.\left(x^2-4x+9\right)=3.\left(x-2\right)^2+15>0\forall x\)
c) \(5x^2-5x+4=5.\left(x^2-x+\dfrac{4}{5}\right)=5.\left(x^2-x+\dfrac{1}{4}+\dfrac{11}{20}\right)=5.\left(x-\dfrac{1}{2}\right)^2+\dfrac{11}{4}>0\forall x\)
d) \(2x^2-2x+9=2.\left(x^2-x+\dfrac{9}{2}\right)=2.\left(x-\dfrac{1}{2}\right)^2+\dfrac{17}{2}>0\forall x\)
Đúng 1
Bình luận (0)
a) = (3x-1)^2+10
Do (3x-1)^2>=0 với mọi x
--> (3x-1)^2+10>0 với mọi x
Đúng 1
Bình luận (0)
a) \(9x^2-6x+11=\left(3x-1\right)^2+10\ge10>0\)
b) \(3x^2-12x+81=3\left(x-2\right)^2+69\ge69>0\)
c) \(5x^2-5x+4=5\left(x-\dfrac{1}{2}\right)^2+\dfrac{11}{4}\ge\dfrac{11}{4}>0\)
d) \(2x^2-2x+9=2\left(x-\dfrac{1}{2}\right)^2+\dfrac{17}{2}\ge\dfrac{17}{2}>0\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời