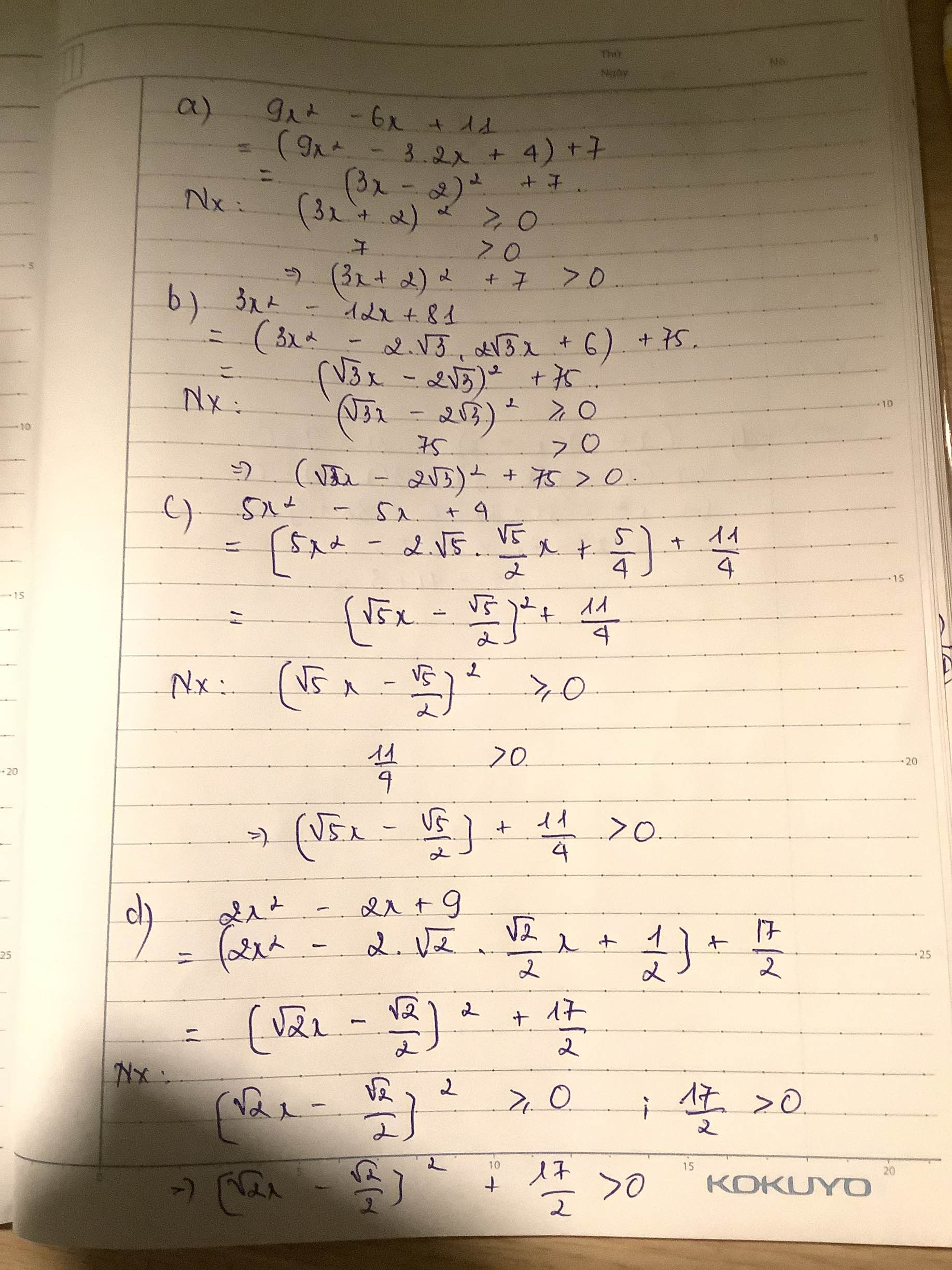a) \(9x^2-6x+11=\left(3x\right)^2-2.3x+1+10=\left(3x-1\right)^2+10>0\forall x\)
b) \(3x^2-12x+81=3.\left(x^2-4x+9\right)=3.\left(x-2\right)^2+15>0\forall x\)
c) \(5x^2-5x+4=5.\left(x^2-x+\dfrac{4}{5}\right)=5.\left(x^2-x+\dfrac{1}{4}+\dfrac{11}{20}\right)=5.\left(x-\dfrac{1}{2}\right)^2+\dfrac{11}{4}>0\forall x\)
d) \(2x^2-2x+9=2.\left(x^2-x+\dfrac{9}{2}\right)=2.\left(x-\dfrac{1}{2}\right)^2+\dfrac{17}{2}>0\forall x\)
a) = (3x-1)^2+10
Do (3x-1)^2>=0 với mọi x
--> (3x-1)^2+10>0 với mọi x
a) \(9x^2-6x+11=\left(3x-1\right)^2+10\ge10>0\)
b) \(3x^2-12x+81=3\left(x-2\right)^2+69\ge69>0\)
c) \(5x^2-5x+4=5\left(x-\dfrac{1}{2}\right)^2+\dfrac{11}{4}\ge\dfrac{11}{4}>0\)
d) \(2x^2-2x+9=2\left(x-\dfrac{1}{2}\right)^2+\dfrac{17}{2}\ge\dfrac{17}{2}>0\)
a: Ta có: \(9x^2-6x+11\)
\(=9x^2-6x+1+10\)
\(=\left(3x-1\right)^2+10>0\forall x\)
b: Ta có: \(3x^2-12x+81\)
\(=3\left(x^2-4x+27\right)\)
\(=3\left(x^2-4x+4+23\right)\)
\(=3\left(x-2\right)^2+69>0\forall x\)