Đáp án C
Đặt t = 2 x 2 − 2 x , t ∈ 0 ; + ∞ ⇒ B P T ⇔ 2 t + t ≥ m 1
Ta có t + 2 t ≥ 2 t . 2 t = 2 2 ⇒ 1 ⇔ m ≤ 2 2
Đáp án C
Đặt t = 2 x 2 − 2 x , t ∈ 0 ; + ∞ ⇒ B P T ⇔ 2 t + t ≥ m 1
Ta có t + 2 t ≥ 2 t . 2 t = 2 2 ⇒ 1 ⇔ m ≤ 2 2
Có tất cả bao nhiêu giá trị của tham số m để bất phương trình log 2 x 2 + m x + m + 2 ≥ log 2 x 2 + 2 nghiệm đúng với mọi x ∈ ℝ
A. 2
B. 4
C. 3
D. 1
Cho bất phương trình m . 3 x + 1 + ( 3 m + 2 ) ( 4 - 7 ) x + ( 4 + 7 ) x > 0 với m là tham số. Tìm tất cả các giá trị của tham số m để bất phương trình đã cho có nghiệm đúng với mọi x ∈ - ∞ ; 0
A. m ≥ 2 - 2 3 3
B. m > 2 - 2 3 3
C. m > 2 + 2 3 3
D. m ≥ - 2 - 2 3 3
Tìm tất cả các giá trị của m để bất phương trình 2 | x - m | + x 2 + 2 > 2 m x thỏa mãn với mọi x
A. m > - 2
B. không tồn tại m
C. - 2 < m < 2
D. m < 2
Có bao nhiêu giá trị nguyên m để bất phương trình sau nghiệm đúng với mọi x ∈ 1 ; 3 : 2 2 x 2 + m x + 1 + 15 ≤ 2 − m + 8 x 2 − 3 x + 2 ?
A. 0.
B. 1.
C. 2.
D. vô số.
Tìm tất cả các giá trị thực của tham số m để bất phương trình ( m + 1 ) x 2 - 2 ( m + 1 ) x + 4 ≥ 0 ( 1 ) có tập nghiệm S = ℝ ?
A. m > - 1
B. - 1 ≤ m ≤ 3
C. - 1 < m ≤ 3
D. - 1 < m < 3
Cho hàm số y=f(x) thoả mãn f(-2)=3, f(2)=2 và bảng xét dấu của đạo hàm như sau:
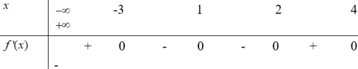
Bất phương trình 3 f ( x ) + m ≤ 4 f ( x ) + 1 + 4 m nghiệm đúng với mọi số thực x ∈ - 2 ; 2 khi và chỉ khi
A. m ∈ - 2 ; - 1
B. m ∈ - 2 ; - 1
C. m ∈ - 2 ; 3
D. m ∈ - 2 ; 3
Bất phương trình 4 x 2 + x - m + 4 x 2 + 2 > 2 2 x 2 + x - m + 2 x nghiệm đúng với mọi số thực x khi và chỉ khi
A. m ∈ ( - ∞ ; - 1 2 )
B. m ∈ - ∞ ; - 1 4
C. m ∈ ( - ∞ ; - 1 4 ]
D. m ∈ - ∞ ; - 1 2
Tìm tất cả các giá trị của m để bất phương trình 3 sin 2 x + cos 2 x sin 2 x + 4 cos 2 x + 1 ≤ m + 1 đúng với mọi x ∈ ℝ
A. m ≥ 3 5 4
B. m ≥ 3 5 + 9 4
C. m ≥ 65 − 9 2
D. m ≥ 65 − 9 4
Tìm tất cả các giá trị của m để bất phương trình 3 sin 2 x + cos 2 x sin 2 x + 4 cos 2 x + 1 ≤ m + 1 đúng với mọi x ∈ ℝ
A. m ≥ 3 5 4
B. m ≥ 3 5 + 9 4
C. m ≥ 65 − 9 2
D. m ≥ 65 − 9 4