Có ![]()
![]()
Đặt t=f(x)+m bất phương trình trở thành: ![]()
![]()
Vậy ![]()
![]()
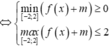
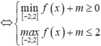
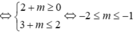
Chọn đáp án B.
Có ![]()
![]()
Đặt t=f(x)+m bất phương trình trở thành: ![]()
![]()
Vậy ![]()
![]()
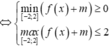
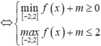
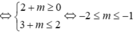
Chọn đáp án B.
Cho hàm số y=f(x) có bảng xét dấu của đạo hàm như sau

Bất phương trình f x < e x 2 + m đúng với mọi x ∈ - 1 ; 1 khi và chỉ khi
A. m ≥ f 0 - 1
B. m > f - 1 - e
C. m > f 0 - 1
D. m ≥ f - 1 - e
Cho hàm số y=f(x) có bảng biến thiên như hình vẽ, biết f(-1)=f(2) và f(0)=f(3)
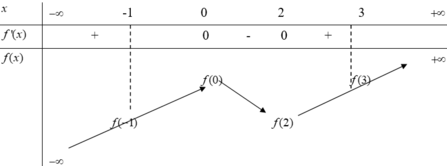
Phương trình f(2sinx+1)=f(m) có đúng ba nghiệm thuộc đoạn - π 2 ; π 2 khi và chỉ khi
A. m ∈ 0 ; 2
B. m ∈ 1 ; 3 \ 0 ; 2
C. m ∈ f ( 2 ) ; f ( 0 )
D. m ∈ - 1 ; 3
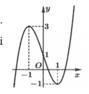
Cho hàm số y = f(x). Hàm số y = f ' x có đồ thị như hình bên. Biết f(-1) = 1, f - 1 e = 2 . Bất phương trình f(x) < ln(-x) + m đúng với mọi x ∈ - 1 ; - 1 e khi và chỉ khi
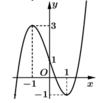
A. m > 2
B. m ≥ 2
C. m > 3
D. m ≥ 3
Cho hàm số y = f(x). Hàm số y = f ' x có đồ thị như hình bên. Biết f - 1 = 1 ; f - 1 e = 2 . Bất phương trình f x < ln - x + m đúng với mọi x ∈ - 1 ; - 1 e khi và chỉ khi
A. m > 2
B. m ≥ 2
C. m > 3
D. m ≥ 3
Cho hàm số y=f(x) có đạo hàm đến cấp hai trên R. Bảng biến thiên của hàm số y=f'(x) như hình vẽ. Bất phương trình m + x 2 ≤ f x + 1 3 x 3 nghiệm đúng với mọi x ∈(0;3) khi và chỉ khi
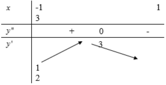
A. m< f (0).
B. m≤ f (3).
C. m≤ f (0).
D. m< f (1)− 2 3
Cho hàm số y=f(x) . Hàm số y= f'(x) có bảng biến thiên như sau

Bất phương trình f ( x ) < ln x + m đúng với mọi x ∈ ( 0 ; 1 ) khi và chỉ khi
A. I = l a a
B. I = l a
C. I = l a ( a - 1 )
D. I = l a ( a + 1 )
Cho hàm số y=f(x). Hàm số y=f' (x) có bảng biến thiên như sau

Bất phương trình f ( e x ) < e 2 x + m nghiệm đúng với mọi x ∈ ( ln 2 ; ln 4 ) khi và chỉ khi
A. m ≥ f ( 2 ) - 4
B. m ≥ f ( 4 ) - 16
C. m > f ( 2 ) - 4
D. m > f ( 4 ) - 16
Cho hàm số y=f(x) thỏa mãn f ’ ( x ) = - x 2 - 2 mọi x thuộc R. Bất phương trình f(x)<m có nghiệm thuộc khoảng (0;1) khi và chỉ khi
A. m ≥ f(1)
B. m ≥ f(0)
C. m > f(0)
D. m > f(1)
Cho hàm số y=f(x). Hàm số y=f'(x) có bảng biến thiên như sau

Bất phương trình f e x < e x + m nghiệm đúng với mọi x ∈ - 1 ; 1 khi và chỉ khi
A. m ≥ f 1 e - 1 e
B. m > f - 1 - 1 e
C. m ≥ f - 1 - 1 e
D. m > f 1 e - 1 e