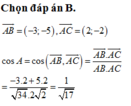trên mặt phẳng oxy cho tam giác abc với A(2;-1) B(-1;2) C(-4;-1) viết phương trình đường tròn ngoại tiếp tam giác abc

Những câu hỏi liên quan
Trên mặt phẳng tọa độ Oxy, cho tam giác ABC biết
A
1
;
3
,
B
-
2
;
-
2
,
C
3
;
1
. Tính cosin góc A của tam giác. A.
cos
A
2...
Đọc tiếp
Trên mặt phẳng tọa độ Oxy, cho tam giác ABC biết A 1 ; 3 , B - 2 ; - 2 , C 3 ; 1 . Tính cosin góc A của tam giác.
A. cos A = 2 17
B. cos A = 1 17
C. cos A = - 2 17
D. cos A = - 1 17
cho mặt phẳng Oxy cho tam giác ABC biết A(1,-3) , B(3,-5) , C(2,-2) : a) tìm M trên Ox sao cho tam giác ABM cân tại M ; b) tìm N trên Oy sao cho tam giác ABN vuông tại A
a) Gọi điểm M(x,0). Ta có MA = MB
=> MA2 = MB2
=> (1 - x)2 + (-3 - 0)2 = (3 - x)2 + (-5 - 0)2
1 - 2x + x2 + 9 = 9 - 6x + x2 + 25
4x = 24
x = 6
Vậy điểm M(6, 0)
b) Gọi N(0, y), ta có NA vuông góc với AB
=> Tích vô hướng giữa hai vector AN và vector AB bằng 0
=> (0 - 1, y + 3) . (3 - 1, -5 + 3) = 0
-2 - 2(y + 3) = 0
y = -4
Vậy N(0, -4)
Đúng 2
Bình luận (0)
Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có A(2;-1), B(4;5) và C(-3;2). Lập phương trình đường cao của tam giác ABC kẻ từ A.
A. 7x + 3y - 11 = 0
B. -3x + 7y + 13 = 0
C. 3x + 7y + 1 = 0
D. 7x + 3y + 13 = 0
Chọn A.
Gọi AH là đường cao của tam giác ABC ⇒ AH ⊥ BC.
B(4;5), C(-3;2) 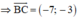
Phương trình đường cao AH đi qua A(2;-1) nhận 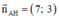 là VTPT là:
là VTPT là:
7.(x - 2) + 3.(y + 1) = 0 ⇔ 7x - 14 + 3y + 3 = 0 ⇔ 7x + 3y - 11 = 0
Vậy phương trình đường cao AH là 7x + 3y - 11 = 0.
Đúng 1
Bình luận (0)
Trên mặt phẳng tọa độ Oxy, cho ba điểm A(– 2; 4), B(– 3; 1), C(1; 5). Diện tích tam giác ABC bằng?
AB (-1,-3)
AC (3,1)
BC (4.4)
Ta co : AB.AC= (-1).(3) + (-3).(1) = 0
suy ra : tam giac ABC vuong tai A
S= 1/2.AB.AC
Ban tu tinh do dai AB, AC nhé
Đúng 1
Bình luận (0)
Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có A(-2;4), B(4;1), C(-2;-1). Tìm tọa độ trực tâm H tam giác.
vecto AH=(x+2;y-4); vecto BC=(-6;-2)
vecto BH=(x-4;y-1); vecto AC=(0;-5)
Theo đề, ta có: -6(x+2)-2(y-4)=0 và 0(x-4)-5(y-1)=0
=>y=1 và -6(x+2)=2(y-4)=2*(1-4)=-6
=>x+2=1 và y=1
=>x=-1 và y=1
Đúng 1
Bình luận (0)
Trong mặt phẳng oxy cho tam giác abc biết A(-1;1),B(3;-2),C(5;1). Tính chu vi Tam giác abc
\(\overrightarrow{AB}=\left(4;-3\right)\Rightarrow AB=5\)
\(\overrightarrow{AC}=\left(6;0\right)\Rightarrow AC=6\)
\(\overrightarrow{BC}=\left(2;3\right)\Rightarrow BC=\sqrt{13}\)
Chu vi tam giác: \(AB+AC+BC=11+\sqrt{13}\)
Đúng 2
Bình luận (0)
Trên mặt phẳng tọa độ Oxy, cho tam giác ABC với tọa độ các đỉnh là A(1; 2), B(3; 4), C(6; 1). Phương trình đường thẳng chứa đường cao AH của tam giác đó có hệ số góc là
duong thang di qua BC la y=-1x+7
=> he so can tim la 1
Đúng 0
Bình luận (0)
Mặt phẳng với hệ tọa độ Oxy cho tam giác ABC có A(2;4); B(5;1); C(-1;-2) Phép tịnh tiến T B C → biến tam giác ABC thành tam giác A’B’C’. Tọa độ trọng tâm của tam giác A’B’C’ là
A. (-4;2)
B. (4;2)
C. (4;-2)
D. (-4;-2)
Trong mặt phẳng oxy cho tam giác abc biết A(2;-1), B(3;-3),C (0;1). Tính chu vi Tam giác abc
\(\overrightarrow{AB}=\left(1;-2\right)\Rightarrow AB=\sqrt{5}\)
\(\overrightarrow{AC}=\left(-2;2\right)\Rightarrow AC=2\sqrt{2}\)
\(BC=\left(-3;4\right)\Rightarrow BC=5\)
Chu vi tam giác ABC: \(AB+AC+BC=\sqrt{5}+2\sqrt{2}+5\)
Đúng 2
Bình luận (0)