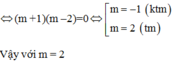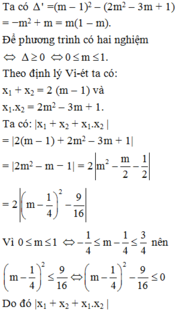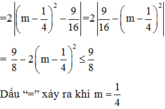Cho phương trình: x2 - 2(m - 1)x + m2 - 3m = 0 . Giải phương trình khi m = −2.

Những câu hỏi liên quan
Cho phương trình: x2 - 2(m - 1)x + m2 - 3m = 0 (1) với m là tham số.
a) Giải phương trình (1) khi m = 0.
b) Tìm giá trị của m để phương trình (1) có hai nghiệm x1, x2 thỏa mãn điều kiện: |x1| - 4 ≥ - |x2|
a) Thay m=0 vào phương trình (1), ta được:
\(x^2-2\cdot\left(0-1\right)x+0^2-3m=0\)
\(\Leftrightarrow x^2+2x=0\)
\(\Leftrightarrow x\left(x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-2\end{matrix}\right.\)
Vậy: Khi m=0 thì S={0;-2}
Đúng 0
Bình luận (1)
Cho phương trình: x2 - 2(m - 1)x + m2 - 3 = 0 . Giải phương trình khi m = −2.
Khi m=-2 thì pt sẽ là:
x^2-2(-2-1)x+(-2)^2-3=0
=>x^2+6x+1=0
=>\(x=-3\pm2\sqrt{2}\)
Đúng 1
Bình luận (0)
Bài1. Cho phương trình : x2 - 2(m - 1)x + m2 - 6 = 0 ( m là tham số )
Giải phương trình khi m = 3
Tìm m để phương trình có 2 nghiệm x1 , x2 thoản mãn x12 + x22 = 16
a. Em tự giải
b.
\(\Delta'=\left(m-1\right)^2-\left(m^2-6\right)=-2m+7\)
Pt đã cho có 2 nghiệm khi: \(-2m+7\ge0\Rightarrow m\le\dfrac{7}{2}\)
Khi đó theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2\left(m-1\right)\\x_1x_2=m^2-6\end{matrix}\right.\)
\(x_1^2+x_2^2=16\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=16\)
\(\Leftrightarrow4\left(m-1\right)^2-2\left(m^2-6\right)=16\)
\(\Leftrightarrow2m^2-8m=0\Rightarrow\left[{}\begin{matrix}m=0\\m=4>\dfrac{7}{2}\left(loại\right)\end{matrix}\right.\)
Vậy \(m=0\)
Đúng 1
Bình luận (0)
Cho phương trình:
x
2
– 2(m – 1)x +
m
2
− 3m 0. Tìm m để phương trình có 2 nghiệm phân biệt
x
1
;
x
2
thỏa mãn
x
1
2
+
x
2
2
8
A. m 2 B....
Đọc tiếp
Cho phương trình: x 2 – 2(m – 1)x + m 2 − 3m = 0. Tìm m để phương trình có 2 nghiệm phân biệt x 1 ; x 2 thỏa mãn x 1 2 + x 2 2 = 8
A. m = 2
B. m = −1
C. m = −2
D. m = 1
Cho phương trình : x2−(m−2)x−m2+3m−4=0x2−(m−2)x−m2+3m−4=0. a. CMR: phương trình có 2 nghiệm trái dấu nhau với mọi m
\(Denta=\left(2m-3\right)^2-4\left(m^2-3m\right)=9< 0\Rightarrow\) pt lluôn có 2 nghiệm pb với mọi x
\(x_1=\frac{\left[2m-3+9\right]}{2}=m+3\)
\(x_2=\frac{\left[2m-3-9\right]}{2}=m-6\)
P/s: Tới đây là dễ rồi, tự giải tiếp nha!
Đúng 0
Bình luận (0)
Cho phương trình x2 -2(m+1)x +m2+2m-3=0(m là than số)
a. giải phương trình khi m=0
b. Chứng tỏ phương trình luôn có 2 nghiệm phân biệt
a, Thay m = 0 vào phương trình trên ta được
\(x^2-2x-3=0\)
\(\Leftrightarrow\left(x-3\right)\left(x+1\right)=0\Leftrightarrow x=-1;x=3\)
Vậy với m = 0 thì x = -1 ; x = 3
Đúng 0
Bình luận (0)
Cho phương trình
x
2
-
2
(
m
-
1
)
x
+
m
2
-
3
m
0
Giả sử phương trình có hai nghiệm
x
1
;
x
2
.Tìm hệ thức giữa
x
1
;
x
2
độc lập đối với m.
Đọc tiếp
Cho phương trình x 2 - 2 ( m - 1 ) x + m 2 - 3 m = 0 Giả sử phương trình có hai nghiệm x 1 ; x 2 .Tìm hệ thức giữa x 1 ; x 2 độc lập đối với m.
![]()
![]()
![]()
![]()
Đáp án: A
Theo hệ thức Vi-ét ta có: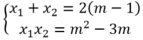
Ta xét các phương án:
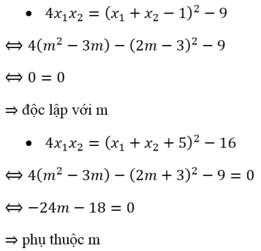
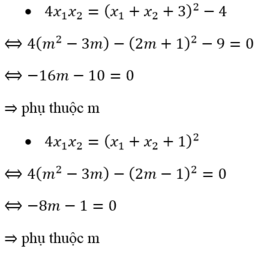
Đúng 0
Bình luận (0)
Cho phương trình
x
2
– (2m + 1)x + 2
m
2
– 3m + 1 0, với m là tham số. Gọi
x
1
;
x
2
là nghiệm của phương trình. Chọn câu đúng. A.
|
x
1
+
x
2
+
...
Đọc tiếp
Cho phương trình x 2 – (2m + 1)x + 2 m 2 – 3m + 1 = 0, với m là tham số. Gọi x 1 ; x 2 là nghiệm của phương trình. Chọn câu đúng.
A. | x 1 + x 2 + x 1 . x 2 | ≤ 9 8
B. | x 1 + x 2 + x 1 . x 2 | ≥ 9 8
C. | x 1 + x 2 + x 1 . x 2 | = 9 8
D. | x 1 + x 2 + x 1 . x 2 | ≥ 2
cho phương trình:
x2 + (2m + 1)x +m2 - 3m = 0 (1)
a) giải phương trình khi x = 1
b) tìm m để phương trình có nghiệm.
a) Thay \(x=1\) vào phương trình, ta được:
\(1+2m+1+m^2-3m=0\) \(\Rightarrow m\in\varnothing\)
Vậy khi \(x=1\) thì phương trình vô nghiệm
b) Xét phương trình, ta có: \(\Delta=16m+1\)
Để phương trình có nghiệm \(\Leftrightarrow\Delta\ge0\) \(\Leftrightarrow m\ge-\dfrac{1}{16}\)
Vậy \(m\ge-\dfrac{1}{16}\)
Đúng 1
Bình luận (0)