!!-Chứng minh an+bn=cn (a,b,c,n ϵ Z; a,b,c≠0; n>2) vô nghiệm.

Những câu hỏi liên quan
Cho tam giác ABC, đường phân giác góc B cắt AC tại M. Từ M vẽ MN song song với AB. N ϵ BC. Chứng minh \(\dfrac{BN}{BA}\)=\(\dfrac{CN}{CB}\)
BN/CN=AM/MC=BA/CB
=>BN/BA=CN/CB
Đúng 0
Bình luận (0)
Chứng minh rằng
a) A = n(3n-1) - 3n(n-2) ⋮ 5 (∀n ϵ R)
b) B = n(n+5) - (n-3)(n+2) ⋮ 6 (∀n ∈ Z)
c) C= (n2 + 3n - 1)(n+2) - n3+2 ⋮ 5 (∀n ϵ Z)
a: A=3n^2-n-3n^2+6n=5n chia hết cho 5
b: B=n^2+5n-n^2+n+6=6n+6=6(n+1) chia hết cho 6
c: =n^3+2n^2+3n^2+6n-n-2-n^3+2
=5n^2+5n
=5(n^2+n) chia hết cho 5
Đúng 0
Bình luận (0)
Cho ΔABC, M ϵ BC sao cho BC = 4cm. Trên AC lấy N sao cho CN : AN = 1 : 3. Chứng minh rằng MN // AB
Bạn coi lại đề giùm mình
bạn phải nói rõ là mc hay là bm bằng bao nhiêu chứ?
Đúng 1
Bình luận (1)
1. cho △ABC có góc A = 90 độ . gọi M là trung điểm AC . trên tia BM lấy điểm N . sao cho M là trung điểm BN . chứng minh
a. CN⊥AC và CN=AB
b. AN=BC và AN//BC
a: Xét tứ giác ABCN có
M là trung điểm chung của AC và BN
Do đó; ABCN là hình bình hành
=>AB=CN và AB//CN
=>CN vuông góc với CA
b: Vì ABCN là hình bình hành
nên AN//BC và AN=BC
Đúng 0
Bình luận (0)
Cho tam giác ABC (AB = AC), M là trung điểm của BC (M ϵ BC) .
a) Chứng minh tam giác ABM = tam giác ACM.
b) Lấy điểm N thuộc đoạn thẳng AM , chứng minh NB = NC.
c) Tia BN cắt AC tại D, tia CN cắt AB tại E. Chứng minh ED // BC.
Lấy điểm H sao cho HB = HC ( H và A nằm trên hai nửa mặt phẳng đối nhau bờ BC). Chứng minh ba điểm A, M, H thẳng hàng.
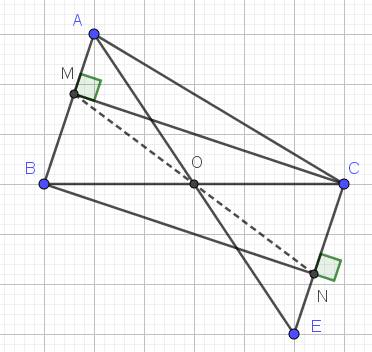
Cho △ABC , O là trung điểm của BC . Trên ria đối của tia OA lấy điểm E sao cho OE = OA .
a) Chứng minh : △AOB = △EOC
b) Chứng minh : AB = EC ; AB // EC
c) Từ C kẻ CM ⊥ AB ( M ϵ AB ) , từ B kẻ BN ⊥ EC ( N ϵ EC ) . Chứng minh ba điểm M , O , N thẳng hàng .
giụp mình vs ạ![]()
Lời giải:
a. Xét tam giác $AOB$ và $EOC$ có:
$\widehat{AOB}=\widehat{EOC}$ (đối đỉnh)
$AO=EO$ (gt)
$OB=OC$ (do $O$ là trung điểm $BC$)
$\Rightarrow \triangle AOB=\triangle EOC$ (c.g.c)
b.
Từ tam giác bằng nhau phần a suy ra:
$AB=EC$ (đpcm)
$\widehat{OAB}=\widehat{OEC}$. Mà 2 góc này ở vị trí so le trong nên $AB\parallel CE$ (đpcm)
c.
Xét tam giác $BMC$ và $CNB$ có:
$\widehat{BMC}=\widehat{CNB}=90^0$
$BC$ chung
$\widehat{MBC}=\widehat{NCB}$ (so le trong)
$\Rightarrow \triangle BMC=\triangle CNB$ (g.c.g)
$\Rightarrow BM=NC$
Xét tam giác $BMO$ và $CNO$ có:
$BM=CN$ (cmt)
$\widehat{MBO}=\widehat{NCO}$ (so le trong)
$BO=CO$
$\Rightarrow \triangle BMO=\triangle CNO$ (c.g.c)
$\Rightarrow \widehat{BOM}=\widehat{CON}$
$\Rightarrow \widehat{BOM}+\widehat{BON}=\widehat{CON}+\widehat{BON}$
$\Rightarrow \widehat{MON}=\widehat{BOC}=180^0$
$\Rightarrow M, O, N$ thẳng hàng.
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A , M là trung điểm của AC . Trên tia BM lấy N sao cho M là trung điểm của BN .
a : Chứng minh CN vuông góc với AC và CN bằng AB .
b : Chứng minh AN song song với BC .
Cho hình bình hành ABCD lấy M sao cho B là trung điểm của AM , lấy điểm N sao cho D là trung điểm của AN . Chứng minh a) M và N đối xứng với nhau qua C b) Ba đường thẳng AB,BN,DM đồng quy c) Gọi BN cắt CD ở O,AO cắt CN ở I.Chứng minh NI=2/3NC
cho tam giác ABC . A=90\(^o\)M là trung điểm của AC . trên tia bm lấy điểm N , sao cho M trung điểm BN
a) chứng minh CN vuông AC và CN=AB
b) chứng minh AN = BC và AN // BC