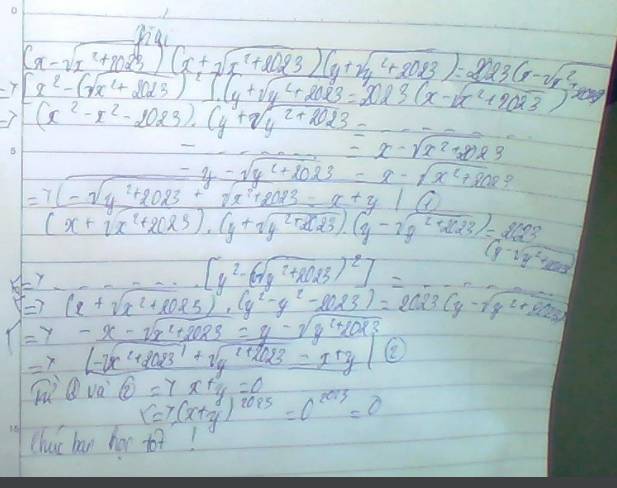Ko tính đc bạn

X=-200

X=-2022 nhà lúc nãy mik nhầm mong bạn thông cảm 

\(\dfrac{2022\times2023-1}{2023\times2021+2022}\)

= \(\dfrac{\left(2021+1\right)\times2023-1}{2023\times2021+2022}\)

= \(\dfrac{2023\times2021+2023-1}{2023\times2021+2022}\)

= \(\dfrac{2023\times2021+2022}{2023\times2021+2022}\)

= 1

2023×2021+20222022×2023−1​

= (2021+1)×2023−12023×2021+20222023×2021+2022(2021+1)×2023−1​

= 2023×2021+2023−12023×2021+20222023×2021+20222023×2021+2023−1​

= 2023×2021+20222023×2021+20222023×2021+20222023×2021+2022​

= 1

Bạn cần viết đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để được hỗ trợ tốt hơn.

Lời giải:
\(\frac{2022\times 2023-3}{2023\times 2021+2020}=\frac{2023\times (2021+1)-3}{2023\times 2021+2020} \\ =\frac{2023\times 2021+2023-3}{2023\times 2021+2020}=\frac{2023\times 2021+2020}{2023\times 2021+2020}=1\)

Để tính (x+y)2023, ta sẽ sử dụng công thức nhân đa thức. Trước tiên, ta mở đuôi công thức:(x+y)2023 = (x+y)(x+y)(x+y)...(x+y)Từ phép nhân đầu tiên, ta có:(x+y)(x+y) = x^2 + 2xy + y^2Tiếp tục nhân với (x+y), ta có:(x^2 + 2xy + y^2)(x+y) = x^3 + 3x^2y + 3xy^2 + y^3Lặp lại quá trình này 2020 lần nữa, ta có:(x^3 + 3x^2y + 3xy^2 + y^3)(x+y) = x^4 + 4x^3y + 6x^2y^2 + 4xy^3 + y^4Tiếp tục nhân với (x+y), ta có:(x^4 + 4x^3y + 6x^2y^2 + 4xy^3 + y^4)(x+y) = x^5 + 5x^4y + 10x^3

Để tính (x+y)2023, ta sẽ sử dụng công thức nhân đa thức. 

Trước tiên, ta mở đuôi công thức:

(x+y)2023 = (x+y)(x+y)(x+y)...(x+y)

Từ phép nhân đầu tiên, ta có:

(x+y)(x+y) = x^2 + 2xy + y^2

Tiếp tục nhân với (x+y), ta có:

(x^2 + 2xy + y^2)(x+y) = x^3 + 3x^2y + 3xy^2 + y^3

Lặp lại quá trình này 2020 lần nữa, ta có:

(x^3 + 3x^2y + 3xy^2 + y^3)(x+y) = x^4 + 4x^3y + 6x^2y^2 + 4xy^3 + y^4

Tiếp tục nhân với (x+y), ta có:

(x^4 + 4x^3y + 6x^2y^2 + 4xy^3 + y^4)(x+y) = x^5 + 5x^4y + 10x^3

- Với \(0< x;y< 1\)

\(x^2>x^{2003}\left(1\right)\)

\(y^2>y^{2003}\left(2\right)\)

\(z^2>z^{2003}\left(3\right)\)

\(\left(1\right)+\left(2\right)+\left(3\right)\Rightarrow M=x^2+y^2+z^2>x^{2003}+y^{2003}+z^{2003}=3\)

\(\Rightarrow\) Không có giá trị max của M.

- Với \(x;y\ge1\)

\(x^2\le x^{2003}\left(1\right)\)

\(y^2\le y^{2003}\left(2\right)\)

\(z^2\le z^{2003}\left(3\right)\)

\(\left(1\right)+\left(2\right)+\left(3\right)\Rightarrow x^2+y^2+z^2\le x^{2003}+y^{2003}+z^{2003}=3\)

\(\Rightarrow Max\left(M\right)=3\left(x=y=z=1\right)\)

Ta có:

\(x^2+5y^2-4x-4xy+6y+5=0\\\Rightarrow[(x^2-4xy+4y^2)-(4x-8y)+4]+(y^2-2y+1)=0\\\Rightarrow[(x-2y)^2-4(x-2y)+4]+(y-1)^2=0\\\Rightarrow(x-2y-2)^2+(y-1)^2=0\)

Ta thấy: \(\left\{{}\begin{matrix}\left(x-2y-2\right)^2\ge0\forall x,y\\\left(y-1\right)^2\ge0\forall y\end{matrix}\right.\)

\(\Rightarrow\left(x-2y-2\right)^2+\left(y-1\right)^2\ge0\forall x,y\)

Mà: \(\left(x-2y-2\right)^2+\left(y-1\right)^2=0\)

nên: \(\left\{{}\begin{matrix}x-2y-2=0\\y-1=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=2y+2\\y=1\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}x=2\cdot1+2=4\\y=1\end{matrix}\right.\)

Thay \(x=4;y=1\) vào \(P\), ta được:

\(P=\left(4-3\right)^{2023}+\left(1-2\right)^{2023}+\left(4+1-5\right)^{2023}\)

\(=1^{2023}+\left(-1\right)^{2023}+0^{2023}\)

\(=1-1=0\)

Vậy \(P=0\) khi \(x=4;y=1\).