
vẽ dùm cái hình với ạ:((

Vẽ dùm e cái hình luôn với ạ đang cần gấp😅
a)
Δ\(ABD\) có \(AM\) là tia phân giác của \(\widehat{ADB}\) \(\left(M\in AB\right)\)
⇒ \(\dfrac{MA}{MB}=\dfrac{DA}{DB}\) (1)
b)
Δ\(ACD\) có \(AN\) là tia phân giác của \(\widehat{ADC}\) \(\left(N\in AC\right)\)
⇒ \(\dfrac{NA}{NC}=\dfrac{DA}{DC}\) (2)
Từ \(\left(1\right)và\left(2\right)\), mà \(BD=CD\left(gt\right)\)
⇒ \(\dfrac{MA}{MB}=\dfrac{NA}{NC}\)
⇒ \(MN\) // \(BC\) \(\left(ĐPCM\right)\)
c)
Δ\(ABC\) có \(MN\) // \(BC\) nên:
⇒ \(\dfrac{AM}{AB}=\dfrac{AN}{AC}\)
⇒ \(AM.AC=AN.AB\)
Ta có: \(MN\) //\(BC\)
⇒ \(\left\{{}\begin{matrix}\widehat{M_1}=\widehat{D_1}\\\widehat{N_1}=\widehat{D_4}\end{matrix}\right.\)
\(Mà\) \(\left\{{}\begin{matrix}\widehat{D_1}=\widehat{D_2}\\\widehat{D_3}=\widehat{D_4}\end{matrix}\right.\)
⇒ \(\left\{{}\begin{matrix}\widehat{M_1}=\widehat{D_2}\\\widehat{N_1}=\widehat{D_3}\end{matrix}\right.\)
Δ\(MKD\) có \(\widehat{M_1}=\widehat{D_2}\) ⇒ \(\text{Δ}MKD\) cân tại K
⇒ \(MK=KD\) \(\left(3\right)\)
Δ\(NKD\) có \(\widehat{N_1}=\widehat{D_3}\) ⇒ \(\text{Δ }NKD\) cân tại K
⇒ \(KN=KD\) \(\left(4\right)\)
Từ (3) và (4) ⇒ \(MK=KN\)
hay K là trung điểm của MN
vẽ hình dùm mình với ạ. Mình cần gấp
Một cái bảnh hình vuông có chu vi 24cm.Hỏi diện tích của cái bảng hình vuông đó bằnh bao nhiêu? Tóm tắt dùm em với ạ
Giải:
Độ dài một cạnh của cái bảng hình vuông là:
\(24:4=6\) (cm)
Diện tích cái bảng hình vuông là:
\(6\times6=36\) (cm2)
Đ/s: ...
Tóm tắt:
Chu vi:24cm
Diện tích:...cm?
Giải
Cạnh của bảng hình vuông là:
24:4=6(cm)
Diện tích hình vuông là:
6x6=36(cm2)
Đ/S: 36cm2
Vẽ hình + ghi gt kl dùm mik với đnag cần gấp ạ
a: Xét ΔOAH vuông tại A và ΔOBH vuông tại B có
OH chung
\(\widehat{AOH}=\widehat{BOH}\)
Do đó: ΔOAH=ΔOBH
Suy ra: OA=OB; AH=BH
b: Xét ΔBHE vuông tại B và ΔAHM vuông tại A có
HB=HA
\(\widehat{BHE}=\widehat{AHM}\)
Do đó: ΔBHE=ΔAHM
Suy ra: HE=HM
c: Ta có: OM=OE
nên O nằm trên đường trung trực của ME(1)
Ta có: HE=HM
nên H nằm trên đường trung trực của ME(2)
Từ (1) và (2) suy ra OH là đường trung trực của ME
dùm mình gấp bài này với ạ ( viết luôn cả gt-kl, vẽ luôn hình )

a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
góc B chung
Do đó: ΔHBA\(\sim\)ΔABC
b: \(BC=\sqrt{AB^2+AC^2}=10\left(cm\right)\)
\(BH=\dfrac{AB^2}{BC}=3.6\left(cm\right)\)
CH=BC-BH=6,4(cm)
 Giúp dùm mik câu b với ạ!! Vẽ hình câu b giúp mik luôn nhé
Giúp dùm mik câu b với ạ!! Vẽ hình câu b giúp mik luôn nhé
a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
góc ABD=góc EBD
=>ΔBAD=ΔBED
=>AD=ED
b: Xét ΔBEF vuông tại E và ΔBAC vuông tại A có
BE=BA
góc EBF chung
=>ΔBEF=ΔBAC
=>BF=BC
2BF=BF+BC>FC
vẽ hình dùm ạ
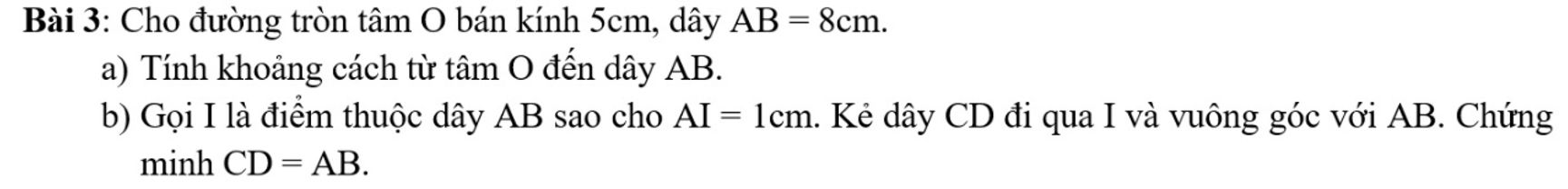
a: Gọi khoảng cách từ O đến AB là OH
=>H là trung điểm của AB
Xét ΔOHB vuông tại H có
\(OB^2=OH^2+HB^2\)
hay OH=3(cm)
cho hình bình hành ABCD. Trên đường chéo BD lấy 2 điểm E và F sao cho DE=BF
CMR:
a) AECF là hình bình hành
b) Gọi M và N lần lượt là giao điểm của AE,CF với DC và AB. CMR AC,BD,MN đồng quy
ai biết vẽ hình vẽ dùm e với ạ khỏi làm câu b cũng được giải dùm e câu a và hình ạ
vẽ hình dùm mình luôn nha mn tks ạ

:a) Điện trở tương đương toàn mạch:
\(R_{12}=\dfrac{R_1.R_2}{R_1+R_2}=\dfrac{60.40}{60+40}=24\left(\Omega\right)\)
b) Vì \(R_1//R_2\Rightarrow U=U_1=U_2=I_{12}.R_{tđ}=0,5.24=12\left(V\right)\)
Cường độ dòng điện qua mỗi điện trở:
\(I_1=\dfrac{U_1}{R_1}=\dfrac{12}{60}=0,2\left(A\right)\\ I_2=\dfrac{U_2}{R_2}=\dfrac{12}{40}=0,3\left(\Omega\right)\)
c) \(\left(R_1//R_2\right)ntR_3\)
Công suất điện R1:
\(P_1=U_1.I_1=12.0,2=2,4\left(W\right)\)
Công suất điện R3:
\(P_3=\dfrac{P_1}{2}=\dfrac{2,4}{2}=1,2\left(W\right)\)
\(R_{12}ntR_3\Rightarrow I_{12}=I_3=0,5\left(A\right)\)
Hiệu điện thế 2 đầu R3:
\(P_3=U_3.I_3\rightarrow U_3=\dfrac{P_3}{I_3}=\dfrac{1,2}{0,5}=2,4\left(V\right)\)
Điện trở R3:
\(R_3=\dfrac{U_3}{I_3}=\dfrac{2,4}{0,5}=4,8\left(\Omega\right)\)
Ko chắc :v