Bài 1: Cho hàm số 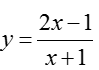
giúp mình bài này ik
Bài 2: : Cho hàm số y= -2x +8
a. Vẽ đồ thị hàm số
b. Tính góc tạo bởi đồ thị hàm số với trục ox?
c. Tính khoảng cách từ gốc tọa độ đến đồ thị hàm số?
d. Điểm A(-1; 10 ) có thuộc đồ thị hàm số không?
e. Tính diện tích và chu vi của hình tạo bởi đồ thị hàm số với hai
trục tọa độ?
Bài tập Cho hàm số y=x-5 có đồ thị (d1) và hàm số y=-2x+1 có đồ thị (d2) a) vẽ (d1) và (d2) trên cùng một mặt phẳng tọa độ b) tìm tọa độ giao điểm của (d1) và (d2) bằng phép toán c) tính khoảng cách từ O đến đường thẳng (d1), khoảng cách từ O đến đường thẳng (d2)
a: 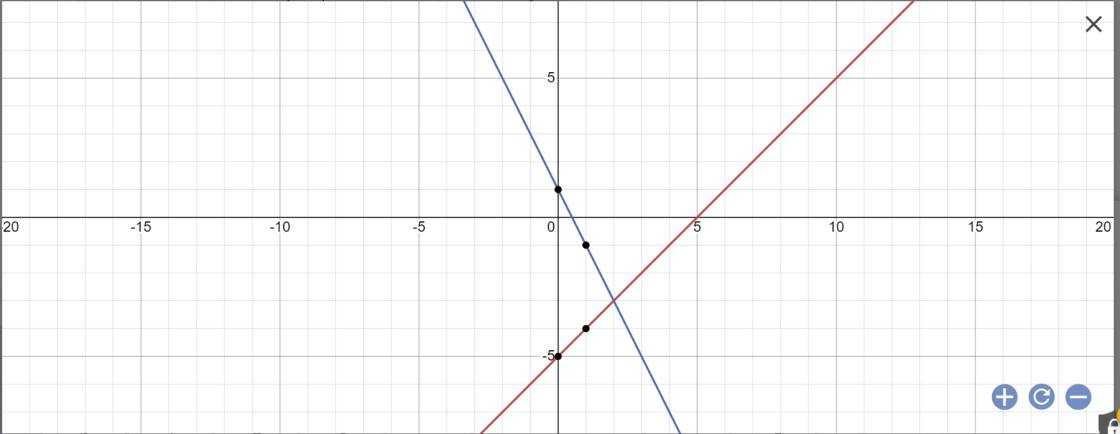
b: Phương trình hoành độ giao điểm là:
-2x+1=x-5
=>-2x-x=-5-1
=>-3x=-6
=>x=2
Thay x=2 vào y=x-5, ta được:
\(y=2-5=-3\)
Vậy: (d1) cắt (d2) tại A(2;-3)
c: (d1): y=x-5
=>x-y-5=0
Khoảng cách từ O(0;0) đến (d1) là:
\(d\left(O;\left(d1\right)\right)=\dfrac{\left|0\cdot1+0\cdot\left(-1\right)-5\right|}{\sqrt{1^2+\left(-1\right)^2}}=\dfrac{5}{\sqrt{2}}\)
(d2): y=-2x+1
=>y+2x-1=0
=>2x+y-1=0
Khoảng cách từ O đến (d2) là:
\(d\left(O;\left(d2\right)\right)=\dfrac{\left|0\cdot2+0\cdot1-1\right|}{\sqrt{2^2+1^2}}=\dfrac{1}{\sqrt{5}}\)
Cho hàm số y = 2 x + 1 x - 1 có đồ thị (C). Có bao nhiêu điểm M thuộc (C) có tung độ nguyên dương sao cho khoảng cách từ M đến tiệm cận đứng bằng 3 lần khoảng cách từ M đến tiệm cận ngang của đồ thị (C)
A. 0
B. 3
C. 2
D. 1
Cho hàm số y = \(\dfrac{2x-1}{x-1}\) đồ thị (C). Viết phương trình tiếp tuyến của (C), biết rằng khoảng cách từ điểm I(1;2) đến tiếp tuyến bằng \(\sqrt{2}\) . Với điểm I như trên, viết phương trình tiếp tuyến của (C) để khoảng cách từ I đến tiếp tuyến Max
\(y'=\dfrac{-1}{\left(x-1\right)^2}\)
Gọi tiếp tuyến qua điểm \(M\left(a;b\right)\) thuộc (C) có dạng:
\(y=\dfrac{-1}{\left(a-1\right)^2}\left(x-a\right)+\dfrac{2a-1}{a-1}\)
\(\Leftrightarrow x+\left(a-1\right)^2y-2a^2+2a-1=0\)
Áp dụng công thức khoảng cách:
\(\dfrac{\left|1+2\left(a-1\right)^2-2a^2+2a-1\right|}{\sqrt{1+\left(a-1\right)^4}}=\sqrt{2}\)
\(\Leftrightarrow\left|2a-2\right|=\sqrt{2}.\sqrt{1+\left(a-1\right)^4}\)
\(\Leftrightarrow2\left(a-1\right)^2=1+\left(a-1\right)^4\)
\(\Leftrightarrow\left[\left(a-1\right)^2-1\right]^2=0\Rightarrow a=...\)
b.
Vẫn từ công thức khoảng cách trên:
\(d=\dfrac{\left|2a-2\right|}{\sqrt{1+\left(a-1\right)^4}}=\dfrac{2\sqrt{\left(a-1\right)^2}}{\sqrt{1+\left(a-1\right)^4}}=\dfrac{2}{\sqrt{\dfrac{1}{\left(a-1\right)^2}+\left(a-1\right)^2}}\)
\(d\le\dfrac{2}{\sqrt{2\sqrt{\dfrac{\left(a-1\right)^2}{\left(a-1\right)^2}}}}=\sqrt{2}\)
Vậy \(d_{max}=\sqrt{2}\) khi tiếp tuyến trùng với các tiếp tuyến câu a
Cho hàm số y = 2 x + 1 x - 1 có đồ thị (C) . Có bao nhiêu điểm M thuộc (C) có tung độ nguyên dương sao cho khoảng cách từ M đến tiệm cận đứng bằng 3 lần khoảng cách từ M đến tiệm cận ngang của đồ thị (C).
A. 0
B. 3
C. 2
D. 1
Cho hàm số \(y=\dfrac{x-2}{x+1}\) và điểm I(-1;1) . Tìm các tiếp tuyến của đồ thị hàm số biết khoảng cách từ điểm I đến tiếp tuyến đó đạt giá trị lớn nhất
\(y'=\dfrac{3}{\left(x+1\right)^2}\Rightarrow\) phương trình tiếp tuyến tại \(M\left(m;\dfrac{m-2}{m+1}\right)\) có dạng:
\(y=\dfrac{3}{\left(m+1\right)^2}\left(x-m\right)+\dfrac{m-2}{m+1}\)
\(\Leftrightarrow3x-\left(m+1\right)^2y+m^2-4m-2=0\)
\(P=d\left(I;d\right)=\dfrac{\left|6m+6\right|}{\sqrt{9+\left(m+1\right)^4}}=\dfrac{6}{\sqrt{\left(m+1\right)^2+\dfrac{9}{\left(m+1\right)^2}}}\le\dfrac{6}{\sqrt{2\sqrt{\dfrac{9\left(m+1\right)^2}{\left(m+1\right)^2}}}}=\sqrt{6}\)
Dấu "=" xảy ra khi và chỉ khi:
\(\left(m+1\right)^2=\dfrac{9}{\left(m+1\right)^2}\Leftrightarrow\left(m+1\right)^2=3\Rightarrow m=\) ... lại xấu :)
Cho hàm số y = 2 x - 1 x + 1 có đồ thị (C) . Biết khoảng cách từ I(-1; 2) đến tiếp tuyến của (C) tại M là lớn nhất thì tung độ của điểm M nằm ở góc phần tư thứ hai, gần giá trị nào nhất?
A.3e
B.2e
C.e
D.4e
+ Ta có y ' = 3 x + 1 2
+ Gọi M x 0 ; 2 x 0 - 1 x 0 + 1 ∈ C , x 0 ≠ - 1 .
Phương trình tiếp tuyến tại M là
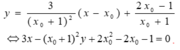
+ 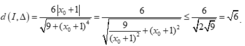
+ Dấu xảy ra khi và chỉ khi
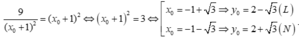
Tung độ này gần với giá trị e nhất trong các đáp án.
Chọn C.
Cho hàm số y = x - 2 x + 1 có đồ thị (C) . Phương trình tiếp tuyến ∆ của đồ thị hàm số (C) tạo với hai đường tiệm cận một tam giác có bán kính đường tròn nội tiếp lớn nhất. Khi đó, khoảng cách từ tâm đối xứng của đồ thị đến ∆ bằng?
A . 3
B . 2 6
C . 2 3
D . 6
+ Đồ thi hàm số đã cho co TCĐ là : x= -1 và TCN là y= 1; tâm đối xứng- giao của 2 đườg tiệm cận có tọa độ là I ( -1; 1)
Gọi M x 0 ; x 0 - 2 x 0 + 1 ∈ C , x 0 ≠ - 1 , I ( - 1 ; 1 )
+ Phương trình tiếp tuyến tại M có dạng
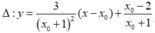
+ Giao điểm của ∆ với tiệm cận đứng là A - 1 ; x 0 - 5 x 0 + 1
+ Giao điểm của ∆ với tiệm cận ngang là B( 2x0+1; 1).
Ta có 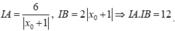
Bán kính đường tròn ngoại tiếp tam giác IAB là S=p.r, suy ra
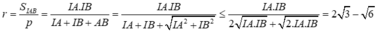
Suy ra,
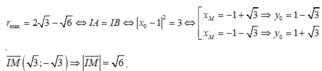
Chọn D.
Cho hàm số y = x x - 1 có đồ thị (C) .Gọi ∆ là tiếp tuyến tại điểm M(x0; y0) (với x0 > 0) thuộc đồ thị (C). Để khoảng cách từ tâm đối xứng I của đồ thị (C) đến tiếp tuyến là lớn nhất thì tung độ của điểm M gần giá trị nào nhất?
A. 7 π 2
B. 3 π 2
C. 5 π 2
D. π 2
+ Hàm số đã cho có TCĐ là x=1 và TCN là y= 1 nên tâm đối xứng- là giao điểm của 2 đường tiệm cận có tọa độ là I (1; 1)
+ Ta có ![]()
Gọi 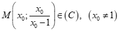
+ Phương trình tiếp tuyến tại M có dạng
![]()
![]()
+ 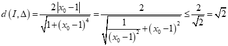
+ Dấu " = " xảy ra khi và chỉ khi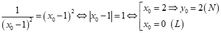
Tung độ này gần với giá trị ![]() nhất trong các đáp án.
nhất trong các đáp án.
Chọn D.