Các câu hỏi tương tự
Cho hàm số
y
2
x
-
1
x
+
1
có đồ thị (C) . Biết khoảng cách từ I(-1; 2) đến tiếp tuyến của (C) tại M là lớn nhất thì tung độ của điểm M nằm ở góc phần tư thứ hai, gần giá trị nào nhất? A.3e B.2e C.e D.4e
Đọc tiếp
Cho hàm số y = 2 x - 1 x + 1 có đồ thị (C) . Biết khoảng cách từ I(-1; 2) đến tiếp tuyến của (C) tại M là lớn nhất thì tung độ của điểm M nằm ở góc phần tư thứ hai, gần giá trị nào nhất?
A.3e
B.2e
C.e
D.4e
Cho hàm số
y
x
x
-
1
có đồ thị (C) .Gọi
∆
là tiếp tuyến tại điểm M(x0; y0) (với x0 0) thuộc đồ thị (C). Để khoảng cách từ tâm đối xứng I của đồ thị (C) đến tiếp tuyến là lớn nhất thì tung độ của điểm M gần giá trị nào nhất? A.
7
π
2
B.
3
π...
Đọc tiếp
Cho hàm số y = x x - 1 có đồ thị (C) .Gọi ∆ là tiếp tuyến tại điểm M(x0; y0) (với x0 > 0) thuộc đồ thị (C). Để khoảng cách từ tâm đối xứng I của đồ thị (C) đến tiếp tuyến là lớn nhất thì tung độ của điểm M gần giá trị nào nhất?
A. 7 π 2
B. 3 π 2
C. 5 π 2
D. π 2
Cho hàm số
y
2
x
+
1
x
-
1
có đồ thị (C) . Gọi I là giao điểm của hai tiệm cận. Tiếp tuyến của (C) cắt 2 tiệm cận tại A và B sao cho chu vi tam giác IAB đạt giá trị nhỏ nhất. Khoảng cách lớn nhất từ gốc tọa độ đến tiếp tuyến
∆
gần giá trị nào nhất? A. 6. B. 4. C. 3. D. 5.
Đọc tiếp
Cho hàm số y = 2 x + 1 x - 1 có đồ thị (C) . Gọi I là giao điểm của hai tiệm cận. Tiếp tuyến của (C) cắt 2 tiệm cận tại A và B sao cho chu vi tam giác IAB đạt giá trị nhỏ nhất. Khoảng cách lớn nhất từ gốc tọa độ đến tiếp tuyến ∆ gần giá trị nào nhất?
A. 6.
B. 4.
C. 3.
D. 5.
Cho hàm số y x4- 2mx2+m (1) với m là tham số thực. Gọi (C) là đồ thị hàm số (1); d là tiếp tuyến của (C) tại điểm có hoành độ bằng 1. Tìm m để khoảng cách từ điểm B( ¾; 1) đến đường thẳng d đạt giá trị lớn nhất? A. 0 B. 1 C. 2 D. 3
Đọc tiếp
Cho hàm số y= x4- 2mx2+m (1) với m là tham số thực. Gọi (C) là đồ thị hàm số (1); d là tiếp tuyến của (C) tại điểm có hoành độ bằng 1. Tìm m để khoảng cách từ điểm B( ¾; 1) đến đường thẳng d đạt giá trị lớn nhất?
A. 0
B. 1
C. 2
D. 3
Tọa độ điểm M thuộc đồ thị (C) của hàm số sao cho khoảng cách từ điểm M đến tiếp tuyến của (C) tại M là lớn nhất là: A. B. C. D.
Đọc tiếp
Tọa độ điểm M thuộc đồ thị (C) của hàm số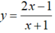 
sao cho khoảng cách từ điểm M đến tiếp tuyến của (C) tại M là lớn
nhất là:
A.
B. 
C. 
D. 
Cho hàm số
y
2
x
-
3
x
-
2
có đồ thị (C) . Biết tiếp tuyến tại M của (C) cắt hai tiệm cận của (C) tại A; B sao cho AB ngắn nhất. Khi đó, độ dài lớn nhất của vectơ
O
M
→
gần giá trị nào nhất ? A. 7. B. 5. C. 6. D. 4.
Đọc tiếp
Cho hàm số y = 2 x - 3 x - 2 có đồ thị (C) . Biết tiếp tuyến tại M của (C) cắt hai tiệm cận của (C) tại A; B sao cho AB ngắn nhất. Khi đó, độ dài lớn nhất của vectơ O M → gần giá trị nào nhất ?
A. 7.
B. 5.
C. 6.
D. 4.
Cho hàm số
y
x
+
2
x
+
1
(C). Gọi d là khoảng cách từ giao điểm hai tiệm cận của đồ thị đến một tiếp tuyến của (C). Giá trị lớn nhất d có thể đạt được là A.
3
3
B.
3
C.
2
D.
2...
Đọc tiếp
Cho hàm số y = x + 2 x + 1 (C). Gọi d là khoảng cách từ giao điểm hai tiệm cận của đồ thị đến một tiếp tuyến của (C). Giá trị lớn nhất d có thể đạt được là
A. 3 3
B. 3
C. 2
D. 2 2
Cho hàm số
y
x
+
1
x
-
2
(C). Gọi d là khoảng cách từ giao điểm của hai đường tiệm cận của đồ thị đến một tiếp tuyến của (C). Giá trị lớn nhất mà d có thể đạt được là: A. B. . C. . D. .
Đọc tiếp
Cho hàm số y = x + 1 x - 2 (C). Gọi d là khoảng cách từ giao điểm của hai đường tiệm cận của đồ thị đến một tiếp tuyến của (C). Giá trị lớn nhất mà d có thể đạt được là:
A. 
B. 
.
C. 
.
D. 
.
Cho hàm số
y
x
+
2
x
+
1
có đồ thị là (C). Gọi d là khoảng cách từ giao điểm 2 tiệm cận của (C) đến một tiếp tuyến bất kỳ của (C). Giá trị lớn nhất d có thể đạt được là: A. . B. . C. . D. .
Đọc tiếp
Cho hàm số y = x + 2 x + 1 có đồ thị là (C). Gọi d là khoảng cách từ giao điểm 2 tiệm cận của (C) đến một tiếp tuyến bất kỳ của (C). Giá trị lớn nhất d có thể đạt được là:
A. 
.
B. 
.
C. 
.
D. 
.