 Giúp mình câu 22 23
Giúp mình câu 22 23

Những câu hỏi liên quan
 Giúp mình câu 21 22 23
Giúp mình câu 21 22 23
Câu 21:
\(C_nH_{2n-2}+AgNO_3+NH_3\rightarrow C_nH_{2n-3}Ag+NH_4NO_3\\ n_X=\dfrac{14-5,44}{108-1}=0,08\left(mol\right)=n_{kết.tủa}\\ M_{C_nH_{2n-3}Ag}=\dfrac{14}{0,08}=175\left(\dfrac{g}{mol}\right)=14n+107\\ \Leftrightarrow n=5\\ \Rightarrow CTPT.X:C_5H_8\\ CTCT:CH\equiv C-CH_2-CH_2-CH_3\\ CH_3-C\equiv C-CH_2-CH_3\\ CH\equiv C-CH\left(CH_3\right)-CH_3\)
Chọn C
Đúng 2
Bình luận (0)
Câu 22:
\(n_{C_2H_2}=\dfrac{2,24}{22,4}=0,1\left(mol\right)\\ C_2H_2+2Br_2\rightarrow C_2H_2Br_4\\ n_{Br_2}=2.n_{C_2H_2}=2.0,1=0,2\left(mol\right)\\ m_{Br_2}=0,2.160=32\left(g\right)\\ Chọn.A\)
Đúng 2
Bình luận (0)
Câu 23:
\( PTHH:C_2H_2+2Br_2\rightarrow C_2H_2Br_4\left(1\right)\\ C_2H_4+Br_2\rightarrow C_2H_4Br_2\left(2\right)\\ C_2H_2+2AgNO_3+2NH_3\rightarrow Ag_2C_2+2NH_4NO_3\\ n_{Ag_2C_2}=\dfrac{18}{240}=0,075=n_{C_2H_2}\\ n_{Br_2\left(tổng\right)}=\dfrac{40}{160}=0,25\left(mol\right)\\ n_{Br_2\left(1\right)}=2.n_{C_2H_2}=2.0,075=0,15\left(mol\right)\\ n_{Br_2\left(2\right)}=0,25-0,15=0,1\left(mol\right)\\ V=V_{C_2H_2\left(đktc\right)}+V_{C_2H_4\left(đktc\right)}=0,075.22,4+0,1.22,4=3,92\left(lít\right)\\ Chọn.A\)
Đúng 2
Bình luận (0)

 câu 21 22 23 24 giúp mình nha
câu 21 22 23 24 giúp mình nha
Giúp mình giải câu 14, 19, 20 21 22 23
CÂU :14. B
CÂU:19. C
CÂU:20. A
CÂU:21. A
22. D
23. B
Đúng 0
Bình luận (0)
làm hộ mình câu 22 23 24
Câu 22:
TXĐ: $(-\infty;0]\cup [2;+\infty)$
BPT \(\Leftrightarrow \left\{\begin{matrix} x\geq -1\\ x^2-2x\leq (x+1)^2\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq -1\\ x\geq \frac{-1}{4}\end{matrix}\right.\Leftrightarrow x\geq \frac{-1}{4}\)
Kết hợp ĐKXĐ suy ra BPT có nghiệm $[\frac{-1}{4};0]\cup [2;+\infty)$
Đúng 1
Bình luận (0)
Câu 23:
Theo công thức trung tuyến:
$CM^2=\frac{BC^2+AC^2}{2}-\frac{AB^2}{4}=\frac{23}{2}$
Áp dụng công thức Herong cho tam giác $ABC$:
$S_{ABC}=\sqrt{\frac{9}{2}(\frac{9}{2}-2)(\frac{9}{2}-3)(\frac{9}{2}-4)}=\frac{3\sqrt{15}}{4}$
$S_{BCM}=\frac{1}{2}S_{ABC}=\frac{3\sqrt{15}}{8}$
Áp dụng công thức: $S=\frac{abc}{4R}$ cho tam giác $BCM$ thì bán kính đường tròn ngoại tiếp tam giác là:
$R=\frac{BC.CM.BM}{4S_{BCM}}=\frac{4.\sqrt{\frac{23}{2}}.1}{\frac{3\sqrt{15}}{2}}=\frac{4\sqrt{690}}{45}$
Đúng 0
Bình luận (0)
Câu 24:
Với $m=-1$ thì BPT $\Leftrightarrow -x-1<0\Leftrightarrow x>-1$ (chứ không phải với mọi $x\in\mathbb{R}$) (loại)
Với $m\neq -1$ thì để $(m+1)x^2+mx+m< 0$ với mọi $x\in\mathbb{R}$ thì:
\(\left\{\begin{matrix} m+1>0\\ \Delta=m^2-4m(m+1)< 0\end{matrix}\right.\Leftrightarrow m>0\)
Vậy $m\in (0;+\infty)$
Đúng 0
Bình luận (0)
Giúp e câu 22 23 đi mn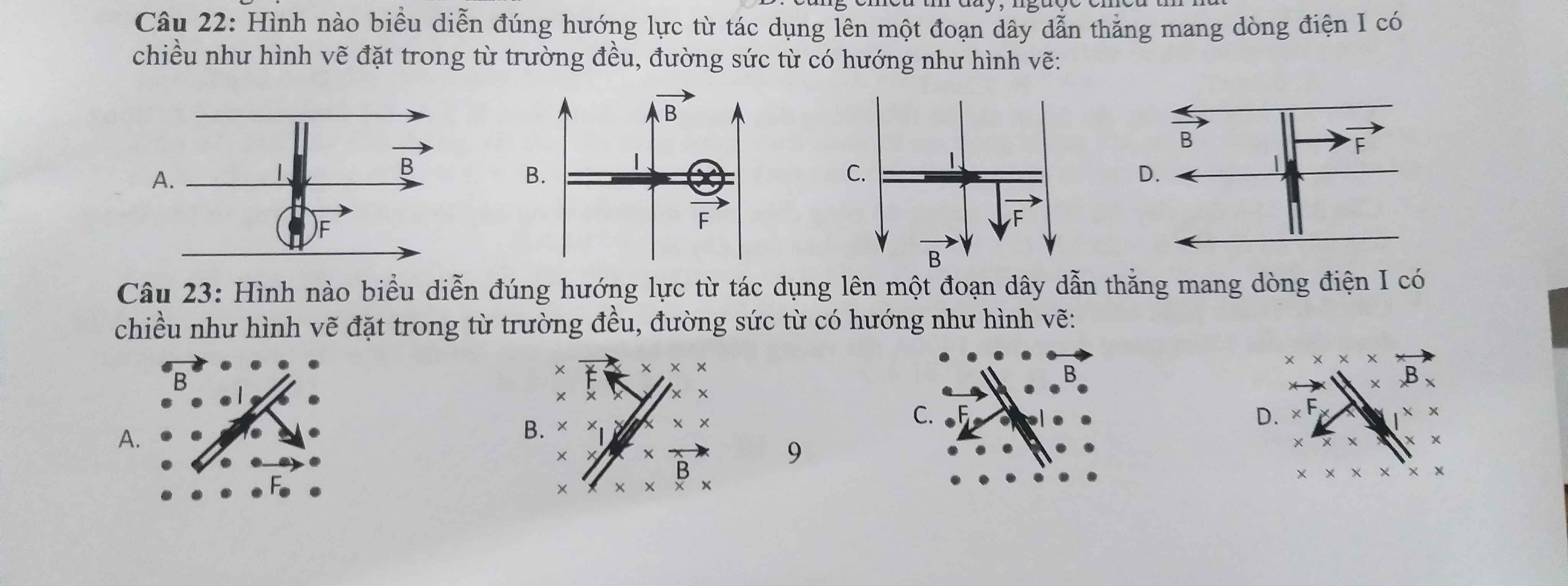
Giúp e câu 22, 23 đi ạ
Rút gọn mỗi biểu thức sau :câu a) A1+3+3^2+3^3+.........................+3^99 +3^100câu b) B2100-299+298-297+....-23+22-2+1mấy cái (/ ) là luỹ thừa giúp mình với mình đang cần
Đọc tiếp
Rút gọn mỗi biểu thức sau :
câu a) A=1+3+3^2+3^3+.........................+3^99 +3^100
câu b) B=2100-299+298-297+....-23+22-2+1
mấy cái (/ ) là luỹ thừa
giúp mình với mình đang cần ![]()
Câu 21. Hệ thống chữ viết của người Hy Lạp cổ đại gồm bao nhiêu chữ cái?
A. 22 chữ cái.
B. 23 chữ cái.
C. 24 chữ cái.
D. 25 chữ cái.
MọI nGưỜi Ơi, GiÚp MìNh VớI
Xem thêm câu trả lời
A =1+2+22+23+ .... +22022
làm nhanh giúp mình
\(A=1+2+2^2+...+2^{2022}\)
\(2A=2\cdot\left(1+2+2^2+...+2^{2022}\right)\)
\(2A=2+2^2+2^3+...+2^{2023}\)
\(2A-A=\left(2+2^2+2^3+...+2^{2023}\right)-\left(1+2+2^2+...+2^{2022}\right)\)
\(A=\left(2-2\right)+\left(2^2-2^2\right)+...+\left(2^{2023}-1\right)\)
\(A=0+0+...+2^{2023}-1\)
\(A=2^{2023}-1\)
Vậy: ...
Đúng 0
Bình luận (0)

























