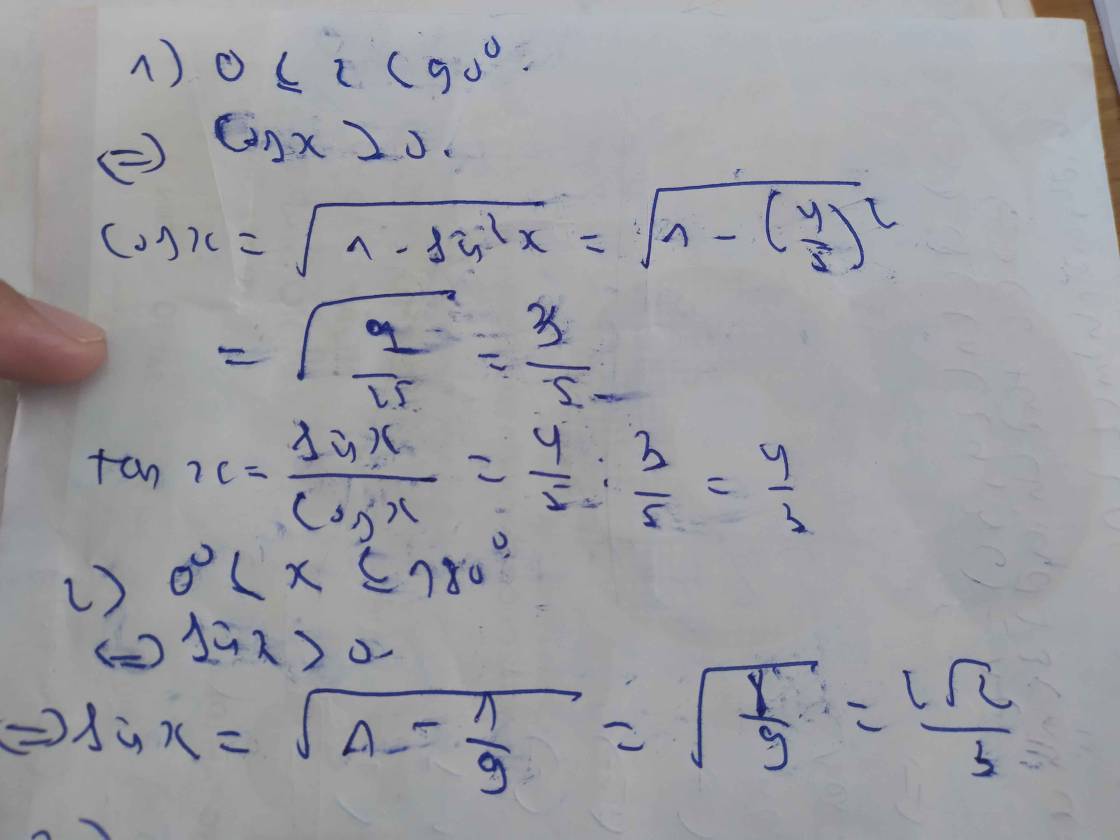Giá trị \(x>0\) thỏa mãn pt \(1+\dfrac{1}{x+2}=\dfrac{12}{x^3+8}\) là x =

Những câu hỏi liên quan
pt: \(x^2-2\left(m-1\right)x+m-3=0\) (m là tham số)
phương trình có hai nghiệm phân biệt tìm giá trị nguyên của m sao cho pt có 2 nghiệm thỏa mãn:
\(\left(\dfrac{1}{x_1}-\dfrac{1}{x_2}\right)^2=\dfrac{\sqrt{11}}{2}\)
Δ=(2m-2)^2-4(m-3)
=4m^2-8m+4-4m+12
=4m^2-12m+16
=4m^2-12m+9+7=(2m-3)^2+7>=7>0 với mọi m
=>Phương trình luôn có hai nghiệm phân biệt
\(\left(\dfrac{1}{x1}-\dfrac{1}{x2}\right)^2=\dfrac{\sqrt{11}}{2}\)
=>\(\dfrac{1}{x_1^2}+\dfrac{1}{x_2^2}-\dfrac{2}{x_1x_2}=\dfrac{\sqrt{11}}{2}\)
=>\(\dfrac{\left(\left(x_1+x_2\right)^2-2x_1x_2\right)}{\left(x_1\cdot x_2\right)^2}-\dfrac{2}{x_1\cdot x_2}=\dfrac{\sqrt{11}}{2}\)
=>\(\dfrac{\left(2m-2\right)^2-2\left(m-3\right)}{\left(-m+3\right)^2}-\dfrac{2}{-m+3}=\dfrac{\sqrt{11}}{2}\)
=>\(\dfrac{4m^2-8m+4-2m+6}{\left(m-3\right)^2}+\dfrac{2}{m-3}=\dfrac{\sqrt{11}}{2}\)
=>\(\dfrac{4m^2-10m+10+2m-6}{\left(m-3\right)^2}=\dfrac{\sqrt{11}}{2}\)
=>\(\sqrt{11}\left(m-3\right)^2=2\left(4m^2-8m+4\right)\)
=>\(\sqrt{11}\left(m-3\right)^2=2\left(2m-2\right)^2\)
=>\(\Leftrightarrow\left(\dfrac{m-3}{2m-2}\right)^2=\dfrac{2}{\sqrt{11}}\)
=>\(\left[{}\begin{matrix}\dfrac{m-3}{2m-2}=\sqrt{\dfrac{2}{\sqrt{11}}}\\\dfrac{m-3}{2m-2}=-\sqrt{\dfrac{2}{\sqrt{11}}}\end{matrix}\right.\)
mà m nguyên
nên \(m\in\varnothing\)
Đúng 2
Bình luận (0)
Câu 22 Giá trị của x thoả mãn 2x(x – 3) + 5(x – 3) 0 là A. 0B.- dfrac{5}{2}C. 3 hoặc -dfrac{5}{2}câu 23 Giá trị của x thoả mãn (10x + 9).x – (5x – 1)(2x + 3) 8 là:A. 1,5B. 1,25C. –1,25D. 3Câu 24 Giá trị của x thỏa mãn 2x( x + 3 ) + 2( x + 3 ) 0 là?A. x -3 hoặc x 1B. x 3 hoặc x -1C. x -3 hoặc x -1 5D. x 1 hoặc x 3 Câu25 Giá trị của x thỏa mãn (x + 2)(x2 – 2x + 4) – x(x2 + 2) 15 là :A. –1,5B. –2,5C. –3,5D. –4,5Câu 26 Giá trị của x thoả mãn (x + 3)3 – x(3x+1)2 + (2x + 1)(4x2 – 2x + 1) 28...
Đọc tiếp
Câu 22 Giá trị của x thoả mãn 2x(x – 3) + 5(x – 3) = 0 là
A. 0
B.- \(\dfrac{5}{2}\)
C. 3 hoặc -\(\dfrac{5}{2}\)
câu 23 Giá trị của x thoả mãn (10x + 9).x – (5x – 1)(2x + 3) = 8 là:
A. 1,5
B. 1,25
C. –1,25
D. 3
Câu 24 Giá trị của x thỏa mãn 2x( x + 3 ) + 2( x + 3 ) = 0 là?
A. x = -3 hoặc x =1
B. x =3 hoặc x = -1
C. x = -3 hoặc x = -1 5
D. x =1 hoặc x = 3 Câu
25 Giá trị của x thỏa mãn (x + 2)(x2 – 2x + 4) – x(x2 + 2) = 15 là :
A. –1,5
B. –2,5
C. –3,5
D. –4,5
Câu 26 Giá trị của x thoả mãn (x + 3)3 – x(3x+1)2 + (2x + 1)(4x2 – 2x + 1) = 28 là: A. 0
B. -8 \(\dfrac{2}{3}\)
C. 0 hoặc 8\(\dfrac{2}{3}\)
D. 0 hoặc -8\(\dfrac{2}{3}\)
Câu 28 Tứ giác ABCD có 𝐴̂ = 1200 ; 𝐵̂ = 800 ; 𝐶̂ = 1000 thì:
A. 𝐷̂ = 600
B. 𝐷̂ = 900
C. 𝐷̂ = 400
D. 𝐷̂ = 1000
Câu 29 Cho ΔABC có I, K lần lượt là trung điểm của AB và AC Biết BC = 20cm. Tacó:
A. IK = 40 cm.
B. IK = 10 cm.
C. IK=5 cm.
D. IK= 15 cm.
\(22,C\\ 23,C\\ 24,Sai.hết\\ 25,C\\ 28,A\\ 29,B\)
Đúng 2
Bình luận (0)
Cho pt \(x^2-2(m-4)x-m^2+4=0\)
Tìm tất cả các giá trị của m để pt có 2 nghiệm \(x_1,x_2\) thỏa mãn \(\dfrac{1}{x_1}+\dfrac{1}{x_2}+\dfrac{4}{x_1x_2}=1\)
Theo Vi et \(\left\{{}\begin{matrix}x_1+x_2=2\left(m-4\right)\\x_1x_2=-m^2+4\end{matrix}\right.\)
\(\dfrac{x_1+x_2}{x_1x_2}+\dfrac{4}{x_1x_2}=1\)
Thay vào ta được : \(\dfrac{2\left(m-4\right)+4}{-m^2+4}=1\Leftrightarrow\dfrac{2m-4}{\left(2-m\right)\left(m+2\right)}=1\Leftrightarrow\dfrac{-2}{m+2}=1\Rightarrow-2=m+2\Leftrightarrow m=-4\)
Đúng 2
Bình luận (0)
1 . Cho pt :x^2-mx+m-10 . Tìm m để pt có 2 nghiệm x_1,x_2 và biểu thức Adfrac{2x_1x_2+3}{x^2_1+x^2_2+2left(x_1x_2+1right)} đạt GTLN2.Giả sử m là giá trị để phương trình x^2-mx+m-20 có 2 nghiệm x_1,x_2 thỏa mãn dfrac{x_1^{^2}-2}{x_1-1}.dfrac{x^2_2-2}{x_2-1}4 . Tìm các giá trị của m
Đọc tiếp
1 . Cho pt :\(x^2-mx+m-1=0\) . Tìm m để pt có 2 nghiệm \(x_1,x_2\) và biểu thức \(A=\dfrac{2x_1x_2+3}{x^2_1+x^2_2+2\left(x_1x_2+1\right)}\) đạt GTLN
2.Giả sử m là giá trị để phương trình \(x^2-mx+m-2=0\) có 2 nghiệm \(x_1,x_2\) thỏa mãn \(\dfrac{x_1^{^2}-2}{x_1-1}.\dfrac{x^2_2-2}{x_2-1}=4\) . Tìm các giá trị của m
1.
\(a+b+c=0\) nên pt luôn có 2 nghiệm
\(\left\{{}\begin{matrix}x_1+x_2=m\\x_1x_2=m-1\end{matrix}\right.\)
\(A=\dfrac{2x_1x_2+3}{x_1^2+x_2^2+2x_1x_2+2}=\dfrac{2x_1x_2+3}{\left(x_1+x_2\right)^2+2}=\dfrac{2\left(m-1\right)+3}{m^2+2}=\dfrac{2m+1}{m^2+2}\)
\(A=\dfrac{m^2+2-\left(m^2-2m+1\right)}{m^2+2}=1-\dfrac{\left(m-1\right)^2}{m^2+2}\le1\)
Dấu "=" xảy ra khi \(m=1\)
2.
\(\Delta=m^2-4\left(m-2\right)=\left(m-2\right)^2+4>0;\forall m\) nên pt luôn có 2 nghiệm pb
Theo Viet: \(\left\{{}\begin{matrix}x_1+x_2=m\\x_1x_2=m-2\end{matrix}\right.\)
\(\dfrac{\left(x_1^2-2\right)\left(x_2^2-2\right)}{\left(x_1-1\right)\left(x_2-1\right)}=4\Rightarrow\dfrac{\left(x_1x_2\right)^2-2\left(x_1^2+x_2^2\right)+4}{x_1x_2-\left(x_1+x_2\right)+1}=4\)
\(\Rightarrow\dfrac{\left(x_1x_2\right)^2-2\left(x_1+x_2\right)^2+4x_1x_2+4}{x_1x_2-\left(x_1+x_2\right)+1}=4\)
\(\Rightarrow\dfrac{\left(m-2\right)^2-2m^2+4\left(m-2\right)+4}{m-2-m+1}=4\)
\(\Rightarrow-m^2=-4\Rightarrow m=\pm2\)
Đúng 1
Bình luận (2)
1) cho góc x (0 độ le x 90 độ) thỏa mãn sinxdfrac{4}{5} giá trị của tanx là 2) cho góc x (0 độ le x le 180 độ) thỏa mãn cosxdfrac{1}{3} giá trị của sinx là3) cho cosxdfrac{1}{2} tính P3sin^2x+4cos^2x
Đọc tiếp
1) cho góc x (0 độ \(\le\) x < 90 độ) thỏa mãn \(sinx=\dfrac{4}{5}\) giá trị của \(tanx\) là
2) cho góc x (0 độ \(\le\) x \(\le\) 180 độ) thỏa mãn \(cosx=\dfrac{1}{3}\) giá trị của \(sinx\) là
3) cho \(cosx=\dfrac{1}{2}\) tính \(P=3sin^2x+4cos^2x\)
Giá trị \(x>0\) thỏa mãn pt \(1+\dfrac{1}{x+2}=\dfrac{12}{x^3+8}\) là x =
\(1+\dfrac{1}{x+2}=\dfrac{12}{x^3+8}\Leftrightarrow\dfrac{\left(x^3+8\right)\left(x+2\right)}{\left(x^3+8\right)\left(x+2\right)}+\dfrac{\left(x^3+8\right)}{\left(x^3+8\right)\left(x+2\right)}=\dfrac{12\left(x+2\right)}{\left(x^3+8\right)\left(x+2\right)}\)
\(\Rightarrow x^4+2x^3+8x+16+x^3+8=12x+24\)
\(\Leftrightarrow x^4+3x^3-4x=0\\ \Leftrightarrow x\left(x^3+3x^2-4\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\left(loại\right)\\x^3+3x^2-4=0\end{matrix}\right.\)
\(x^3+3x^2-4=0\Leftrightarrow\left(x^3+4x^2+4x\right)-\left(x^2+4x+4 \right)=0\)
\(\left(x-1\right)\left(x^2+4x+4\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x-1=0\\x^2+4x+4=0\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=1\\\left(x+2\right)^2=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=1\\x=-2\left(loại\right)\end{matrix}\right.\)
vậy phương trình có tập nghiệm là S={1}
Đúng 0
Bình luận (0)
a)Có bao nhiêu giá trị nguyên dương x thỏa mãn \(\dfrac{x+3}{x^2-4}-\dfrac{1}{x+2}< \dfrac{2x}{2x-x^2}\)
b) Tập nghiệm S của bất pt \(\dfrac{-2x^2+7x+7}{x^2-3x-10}\le-1\)
a) Cho x,y,z là các số dương thỏa mãn x2+y2+z23, tìm giá trị nhỏ nhất của Fdfrac{x^2+1}{z+2}+dfrac{y^2+1}{x+2}+dfrac{z^2+1}{y+2}
b) Với a,b,c 0 thỏa mãn ab+bc+ca3, chứng minh rằng
sqrt{dfrac{a}{a+3}} +sqrt{dfrac{b}{b+3}}+sqrt{dfrac{c}{c+3}}ledfrac{3}{2}
Đọc tiếp
a) Cho x,y,z là các số dương thỏa mãn x2+y2+z2=3, tìm giá trị nhỏ nhất của F=\(\dfrac{x^2+1}{z+2}\)+\(\dfrac{y^2+1}{x+2}\)+\(\dfrac{z^2+1}{y+2}\)
b) Với a,b,c > 0 thỏa mãn ab+bc+ca=3, chứng minh rằng
\(\sqrt{\dfrac{a}{a+3}}\) +\(\sqrt{\dfrac{b}{b+3}}\)+\(\sqrt{\dfrac{c}{c+3}}\)\(\le\)\(\dfrac{3}{2}\)
Cho biểu thức A=(\(\dfrac{x^2}{x^3-4x}+\dfrac{6}{6-3x}+\dfrac{1}{x+2}\)):(x-2 + \(\dfrac{10-x^2}{x+2}\))
a)Rút gọn A
b)Tính giá trị x của A với giá trị của x thỏa mãn |2x-1|=3
c) Tìm x để (3-4x).A<3
d) Tìm giá trị nhỏ nhất của biểu thức B=(8-\(^{x^3}\)).A+x