Cho hình vẽ a) Chứng tỏ AD ||BC. b) Tính số đo C.

Những câu hỏi liên quan
Cho hình vẽ biết CBO=35°, OBD=40° a) Chứng minh AD// BC b) Tính số đo của AOB c) Nếu A= 30° để OA vuông góc với OB thì BC bằng bao nhiêu
Hình như bài này có hình vẽ đúng ko bn??Lm ơn đăng nó lên dùm mk cái!
Đúng 0
Bình luận (0)
Cho hình vẽ biết CBO35°, OBD40° a) Chứng minh AD// BC b) Tính số đo của AOB c) Nếu A 30° để OA vuông góc với OB thì BC bằng bao nhiêu
Đọc tiếp
Cho hình vẽ biết CBO=35°, OBD=40° a) Chứng minh AD// BC b) Tính số đo của AOB c) Nếu A= 30° để OA vuông góc với OB thì BC bằng bao nhiêu
\(a,\left\{{}\begin{matrix}AD\perp CD\\BC\perp CD\end{matrix}\right.\Rightarrow AD\text{//}BC\\ b,\text{Kẻ Oz//AD thì Oz//BC}\\ \Rightarrow\widehat{AOz}=\widehat{OAD}=40^0;\widehat{BOz}=\widehat{OBC}=35^0\left(\text{so le trong}\right)\\ \Rightarrow\widehat{AOB}=\widehat{AOz}+\widehat{BOz}=75^0\\ c,\text{Đề không rõ ràng}\)
Đúng 1
Bình luận (0)
cho tam giác abc,trên nửa mặt bờ ac không chứa điểm b vẽ tia ad//bc.trên nửa mặt phẳng đối với nửa mặt phẳng đó vẽ tia ae//bc
a)chứng tỏ ab//he
b)tính số đo góc ehc
Cho hình vẽ sau:
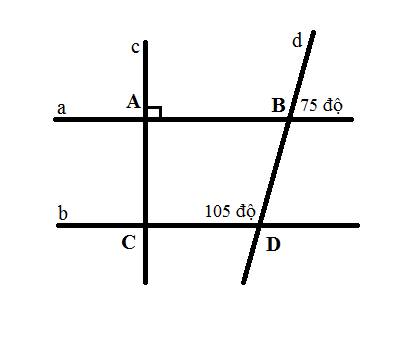
a) Tính số đo góc ABD?
b) Chứng minh a//b
c) Chứng minh \(c\perp b\)
a) Do \(\widehat{ABD}\) đổi đỉnh với góc bên ngoài
\(\Rightarrow\widehat{ABD}=75^o\)
b) Ta có \(\widehat{ABd}=180^o-75^o=105^o\) (kể bù)
\(\Rightarrow\widehat{\text{C}DB}=\widehat{ABd}=105^o\)
Mà hai góc này ở vị trí đồng vị
\(\Rightarrow a//b\)
d) Ta có: \(a//b\) và \(a\perp c\)
\(\Rightarrow b\perp c\)
Đúng 1
Bình luận (0)
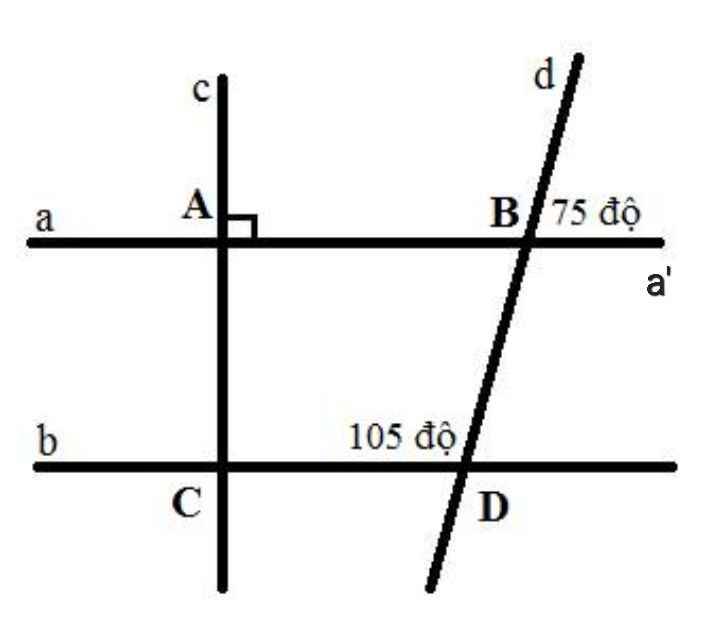 a) Do ∠ABD và ∠dBa' là hai góc đối đỉnh
a) Do ∠ABD và ∠dBa' là hai góc đối đỉnh
⇒ ∠ABD = ∠dBa' = 75⁰
b) Ta có:
∠ABD + ∠a'BD = 180⁰ (kề bù)
⇒ ∠a'BD = 180⁰ - ∠ABD
= 180⁰ - 75⁰
= 105⁰
⇒ ∠a'BD = ∠CDB = 105⁰
Mà ∠a'BD và ∠CDB là hai góc so le trong
⇒ a // b
c) Do c ⊥ a (gt)
a // b (cmt)
⇒ c ⊥ b
Đúng 2
Bình luận (0)
Cho ∆ABC vuông tại A, có ^C=36°.
a) Tính số đo góc B.
b) Gọi M là trung điểm của AC. Qua C kẻ đường vuông góc với AC cắt tia BM tại D. Chứng minh ∆ABM=∆CDM.
c) Chứng minh AD // BC
*Vẽ hình giúp mình luôn nha please*
Xem chi tiết
a) Ta có: ΔABC vuông tại A(gt)
⇔\(\widehat{B}+\widehat{C}=90^0\)(hai góc nhọn phụ nhau)
⇔\(\widehat{B}=90^0-\widehat{C}=90^0-36^0\)
hay \(\widehat{B}=54^0\)
Vậy: \(\widehat{B}=54^0\)
b) Xét ΔAMB vuông tại A và ΔCMD vuông tại C có
AM=CM(M là trung điểm của AC)
\(\widehat{AMB}=\widehat{CMD}\)(hai góc đối đỉnh)
Do đó: ΔAMB=ΔCMD(cạnh góc vuông-góc nhọn kề)
c) Ta có: ΔAMB=ΔCMD(cmt)
nên MB=MD(hai cạnh tương ứng)
Xét ΔAMD và ΔCMB có
MD=MB(cmt)
\(\widehat{AMD}=\widehat{CMB}\)(hai góc đối đỉnh)
MA=MC(M là trung điểm của AC)
Do đó: ΔAMD=ΔCMB(c-g-c)
Suy ra: \(\widehat{MAD}=\widehat{MCB}\)(hai góc tương ứng)
mà \(\widehat{MAD}\) và \(\widehat{MCB}\) là hai góc ở vị trí so le trong
nên AD//BC(Dấu hiệu nhận biết hai đường thẳng song song)
Đúng 2
Bình luận (0)
Cho tứ giác lồi ABCD có góc A = góc B = 90độ và góc C = 3 góc D
a) Vẽ hình và chứng minh 2 cạnh AD và BC song song
b) Tính số đo góc C và góc D
Bạn tự vẽ hình nha ==''
a.
AB _I_ BC
AB _I_ AD
=> AD // BC
b.
AD // BC
=> C + D = 1800 (2 góc kề bù)
\(C=3D\Rightarrow\frac{C}{3}=\frac{D}{1}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{C}{3}=\frac{D}{1}=\frac{C+D}{3+1}=\frac{180^0}{4}=45^0\)
\(\frac{C}{3}=45^0\Rightarrow C=45^0\times3=135^0\)
\(\frac{D}{1}=45^0\Rightarrow D=45^0\)
Chúc bạn học tốt ^^
Đúng 0
Bình luận (0)
Cho 2 góc kề bù CBA và góc DBC với góc CBA = 118o
a, Tính số đo góc DBC
b, Trên cùng nửa mặt phẳng bờ AD chứa tia BC vẽ góc DBM = 31o
c, Chứng tỏ rằng BM là tia phân giác của góc DBC
( vẽ hình nữa ạ)
Bãi 4) Cho tam giác ABC có AB = 6cm; AC = 8cm; BC = 10cm. a) Chứng tỏ tam giác ABC vuông b) Vẽ đường cao AH của tam giác ABC. Tính AH; HC và số đo góc B. c) Gọi E; E lần lượt là hình chiếu của H lên AB; AC. Chứng minh: BH^3 = BE^2.BC.
Cho hình vẽ có a song song b; b song song c và góc A1=125 độ. Chứng tỏ a song song c. Tính số đo góc B2 và góc C1


















