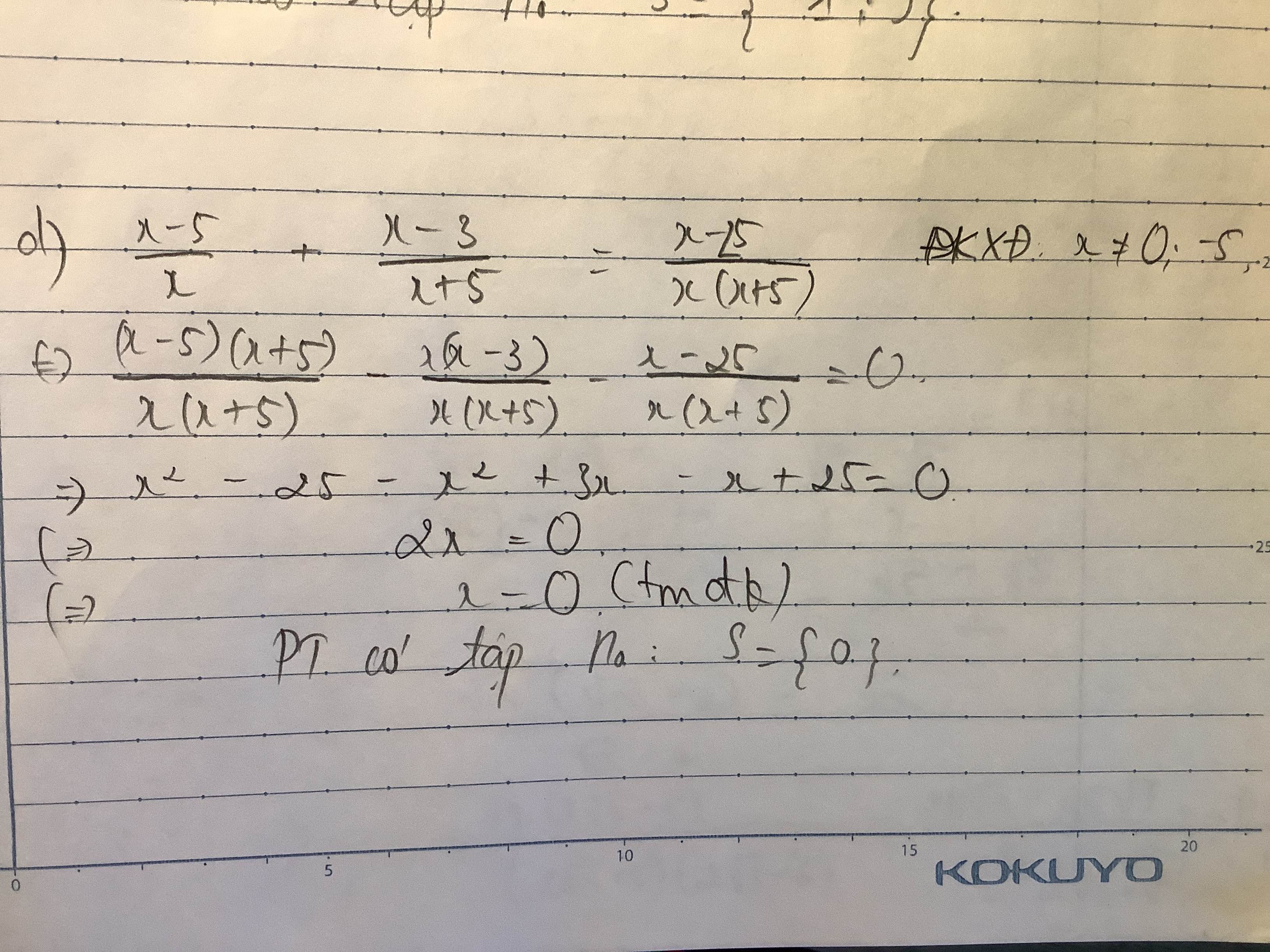\(=\dfrac{4\left(x+3\right)^2}{\left(x+5\right)\left(5x+5\right)}-\dfrac{x^2-25}{\left(3x-2x-5\right)\left(3x+2x+5\right)}-\dfrac{\left(3x-3-x\right)\left(3x-3+x\right)}{\left(4x+15-x\right)\left(4x+15+x\right)}\)

\(=\dfrac{4\left(x+3\right)^2}{5\left(x+1\right)\left(x+5\right)}-\dfrac{x^2-25}{\left(x-5\right)\cdot5\left(x+1\right)}-\dfrac{\left(2x-3\right)\left(4x-3\right)}{3\left(x+5\right)\cdot5\left(x+3\right)}\)

\(=\dfrac{4\left(x+3\right)^2}{5\left(x+1\right)\left(x+5\right)}-\dfrac{\left(x+5\right)}{5\left(x+1\right)}-\dfrac{\left(2x-3\right)\left(4x-3\right)}{15\left(x+5\right)\left(x+3\right)}\)

\(=\dfrac{4\left(x+3\right)^2-\left(x+5\right)\left(x+1\right)}{5\left(x+1\right)\left(x+5\right)}-\dfrac{\left(2x-3\right)\left(4x-3\right)}{15\left(x+3\right)\left(x+5\right)}\)

\(=\dfrac{4x^2+24x+36-x^2-6x-5}{5\left(x+1\right)\left(x+5\right)}-\dfrac{\left(2x-3\right)\left(4x-3\right)}{15\left(x+3\right)\left(x+5\right)}\)

\(=\dfrac{3x^2+18x+31}{5\left(x+1\right)\left(x+5\right)}-\dfrac{\left(2x-3\right)\left(4x-3\right)}{15\left(x+3\right)\left(x+5\right)}\)

\(=\dfrac{3\left(x+3\right)\left(3x^2+18x+31\right)-\left(2x-3\right)\left(4x-3\right)\left(x+1\right)}{15\left(x+3\right)\left(x+5\right)\left(x+1\right)}\)

\(=\dfrac{\left(3x+9\right)\left(3x^2+18x+31\right)-\left(8x^2-18x+9\right)\left(x+1\right)}{15\left(x+3\right)\left(x+5\right)\left(x+1\right)}\)

\(=\dfrac{9x^3+81x^2+255x+279-\left(8x^3+8x^2-18x^2-18x+9x+9\right)}{15\left(x+3\right)\left(x+5\right)\left(x+1\right)}\)

\(=\dfrac{9x^3+81x^2+255x+279-\left(8x^3-10x^2-9x+9\right)}{15\left(x+3\right)\left(x+5\right)\left(x+1\right)}\)

\(=\dfrac{x^3+91x^2+264x+270}{15\left(x+3\right)\left(x+5\right)\left(x+1\right)}\)

a) Ta có: \(\left(x^2-16\right)\left(\dfrac{x}{4}-\dfrac{4x+5}{3}\right)=0\)

\(\Leftrightarrow\left(x-4\right)\left(x+4\right)\left(\dfrac{3x-16x-20}{12}\right)=0\)

\(\Leftrightarrow\left(x-4\right)\left(x+4\right)\cdot\left(-13x-20\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x-4=0\\x+4=0\\-13x-20=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=4\\x=-4\\-13x=20\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=4\\x=-4\\x=\dfrac{-20}{13}\end{matrix}\right.\)

Vậy: \(x\in\left\{4;-4;\dfrac{-20}{13}\right\}\)

b) Ta có: \(\left(4x-1\right)\left(x+5\right)=x^2-25\)

\(\Leftrightarrow\left(4x-1\right)\left(x+5\right)-\left(x^2-25\right)=0\)

\(\Leftrightarrow\left(4x-1\right)\left(x+5\right)-\left(x+5\right)\left(x-5\right)=0\)

\(\Leftrightarrow\left(x+5\right)\left(4x-1-x+5\right)=0\)

\(\Leftrightarrow\left(x+5\right)\left(3x+4\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x+5=0\\3x+4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-5\\3x=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-5\\x=-\dfrac{4}{3}\end{matrix}\right.\)

Vậy: \(x\in\left\{-5;\dfrac{-4}{3}\right\}\)

c) Ta có: \(x\left(x+3\right)^3-\dfrac{x}{4}\cdot\left(x+3\right)=0\)

\(\Leftrightarrow\left(x+3\right)\cdot\left[x\left(x+3\right)^2-\dfrac{1}{4}x\right]=0\)

\(\Leftrightarrow\left(x+3\right)\left[x\left(x^2+6x+9\right)-\dfrac{1}{4}x\right]=0\)

\(\Leftrightarrow\left(x+3\right)\left(x^3+6x^2+9x-\dfrac{1}{4}x\right)=0\)

\(\Leftrightarrow\left(x+3\right)\cdot x\cdot\left(x^2+6x+\dfrac{35}{4}\right)=0\)

\(\Leftrightarrow x\left(x+3\right)\left(x^2+6x+9-\dfrac{1}{4}\right)=0\)

\(\Leftrightarrow x\left(x+3\right)\left[\left(x+3\right)^2-\dfrac{1}{4}\right]=0\)

\(\Leftrightarrow x\left(x+3\right)\left(x+3-\dfrac{1}{2}\right)\left(x+3+\dfrac{1}{2}\right)=0\)

\(\Leftrightarrow x\left(x+3\right)\left(x+\dfrac{5}{2}\right)\left(x+\dfrac{7}{2}\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x+3=0\\x+\dfrac{5}{2}=0\\x+\dfrac{7}{2}=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-3\\x=-\dfrac{5}{2}\\x=-\dfrac{7}{2}\end{matrix}\right.\)

Vậy: \(x\in\left\{0;-3;-\dfrac{5}{2};-\dfrac{7}{2}\right\}\)

a: Ta có: \(4x-2\left(1-x\right)=5\left(x-4\right)\)

\(\Leftrightarrow4x-2+2x=5x-20\)

\(\Leftrightarrow x=-18\)

b: Ta có: \(\dfrac{x}{6}+\dfrac{1-3x}{9}=\dfrac{-x+1}{12}\)

\(\Leftrightarrow6x+4\left(1-3x\right)=3\left(-x+1\right)\)

\(\Leftrightarrow6x+4-12x=-3x+3\)

\(\Leftrightarrow-3x=-1\)

hay \(x=\dfrac{1}{3}\)

c: Ta có: \(\left(x+2\right)^2-3\left(x+2\right)=0\)

\(\Leftrightarrow\left(x+2\right)\left(x-1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=1\end{matrix}\right.\)

d: Ta có: \(\dfrac{x-5}{x}+\dfrac{x-3}{x+5}=\dfrac{x-25}{x\left(x+5\right)}\)

\(\Leftrightarrow x^2-25+x^2-3x=x-25\)

\(\Leftrightarrow2x^2-4x=0\)

\(\Leftrightarrow2x\left(x-2\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\left(loại\right)\\x=2\left(nhận\right)\end{matrix}\right.\)

1) \(\dfrac{A\left(x-5\right)}{\left(x+1\right)\left(x-5\right)}=\dfrac{3x\left(x+3\right)}{\left(x+1\right)\left(x+3\right)}\)

\(\Rightarrow A=3x\)

2) \(\dfrac{\left(x+3\right)\left(x-2\right)}{A\left(x-3\right)}=\dfrac{\left(5x-1\right)\left(x-2\right)}{\left(5x-1\right)\left(x^2+3\right)}\)

\(\Leftrightarrow\dfrac{\left(x+3\right)}{A\left(x-3\right)}=\dfrac{1}{\left(x^2+3\right)}\)

\(\Rightarrow A=\dfrac{\left(x^2+3\right)\left(x+3\right)}{x-3}\)

3) \(\dfrac{\left(x-5\right)\left(x+5\right)}{\left(x+5\right)\left(2x-3\right)}=\dfrac{\left(x-5\right)A}{\left(2x-3\right)\left(x+2\right)}\)

\(\Leftrightarrow1=\dfrac{A}{\left(x+2\right)}\)

\(\Leftrightarrow A=x+2\)

đK: \(x\ge0;x\ne25;x\ne9\)

\(=\left[\dfrac{\sqrt{x}\left(\sqrt{x}-5\right)}{\left(\sqrt{x}-5\right)\left(\sqrt{x}+5\right)}-1\right]:\left[\dfrac{25-x}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-3\right)}-\dfrac{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-3\right)}+\dfrac{\left(\sqrt{x}-5\right)\left(\sqrt{x}+5\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+5\right)}\right]\)

\(=\left[\dfrac{\sqrt{x}}{\sqrt{x}+5}-1\right]:\dfrac{25-x-\left(x-9\right)+\left(x-25\right)}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-3\right)}\)

\(=\dfrac{-5}{\sqrt{x}+5}:\dfrac{9-x}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-3\right)}\)

\(=\dfrac{-5}{\sqrt{x}+5}:\dfrac{-\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-3\right)}\)\(=\dfrac{-5}{\sqrt{x}+5}:\dfrac{-\sqrt{x}-3}{\sqrt{x}+5}\)

\(=\dfrac{-5}{\sqrt{x}+5}:\dfrac{\sqrt{x}+5}{-\left(\sqrt{x}+3\right)}=\dfrac{5}{\sqrt{x}+3}\)

ai giúp với ạ :<

2: Ta có: \(A=\left(\dfrac{1}{\sqrt{a}-1}-\dfrac{1}{\sqrt{a}}\right):\left(\dfrac{\sqrt{a}+1}{\sqrt{a}-2}-\dfrac{\sqrt{a}+2}{\sqrt{a}-1}\right)\)

\(=\dfrac{\sqrt{a}-\sqrt{a}+1}{\sqrt{a}\left(\sqrt{a}-1\right)}:\dfrac{a-1-a+4}{\left(\sqrt{a}-2\right)\left(\sqrt{a}-1\right)}\)

\(=\dfrac{1}{\sqrt{a}\left(\sqrt{a}-1\right)}\cdot\dfrac{\left(\sqrt{a}-2\right)\left(\sqrt{a}-1\right)}{3}\)

\(=\dfrac{\sqrt{a}-2}{3\sqrt{a}}\)

1: Ta có: \(A=\left(\dfrac{x-5\sqrt{x}}{x-25}-1\right):\left(\dfrac{25-x}{x+2\sqrt{x}-15}-\dfrac{\sqrt{x}+3}{\sqrt{x}+5}-\dfrac{\sqrt{x}-5}{\sqrt{x}-3}\right)\)

\(=\left(\dfrac{x-5\sqrt{x}-x+25}{\left(\sqrt{x}-5\right)\left(\sqrt{x}+5\right)}\right):\dfrac{25-x-x+9-x+25}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-3\right)}\)

\(=\dfrac{-5}{\sqrt{x}+5}\cdot\dfrac{\left(\sqrt{x}+5\right)\left(\sqrt{x}-3\right)}{-3x+59}\)

\(=\dfrac{-5\left(\sqrt{x}-3\right)}{-3x+59}\)

\(=\dfrac{5\sqrt{x}-15}{3x-59}\)

1: Ta có: \(A=\left(\dfrac{x-5\sqrt{x}}{x-25}-1\right):\left(\dfrac{25-x}{x+2\sqrt{x}-15}-\dfrac{\sqrt{x}+3}{\sqrt{x}+5}-\dfrac{\sqrt{x}-5}{\sqrt{x}-3}\right)\)

\(=\left(\dfrac{x-5\sqrt{x}-x+25}{\left(\sqrt{x}-5\right)\left(\sqrt{x}+5\right)}\right):\dfrac{25-x-x+9-x+25}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-3\right)}\)

\(=\dfrac{-5}{\sqrt{x}+5}\cdot\dfrac{\left(\sqrt{x}+5\right)\left(\sqrt{x}-3\right)}{-3x+59}\)

\(=\dfrac{-5\left(\sqrt{x}-3\right)}{-3x+59}\)

\(=\dfrac{5\sqrt{x}-15}{3x-59}\)​

2: Ta có: \(A=\left(\dfrac{1}{\sqrt{a}-1}-\dfrac{1}{\sqrt{a}}\right):\left(\dfrac{\sqrt{a}+1}{\sqrt{a}-2}-\dfrac{\sqrt{a}+2}{\sqrt{a}-1}\right)\)

\(=\dfrac{\sqrt{a}-\sqrt{a}+1}{\sqrt{a}\left(\sqrt{a}-1\right)}:\dfrac{a-1-a+4}{\left(\sqrt{a}-2\right)\left(\sqrt{a}-1\right)}\)

\(=\dfrac{1}{\sqrt{a}\left(\sqrt{a}-1\right)}\cdot\dfrac{\left(\sqrt{a}-2\right)\left(\sqrt{a}-1\right)}{3}\)

\(=\dfrac{\sqrt{a}-2}{3\sqrt{a}}\)

3: Ta có: \(A=\left(\dfrac{\sqrt{x}+2}{x+2\sqrt{x}+1}-\dfrac{\sqrt{x}-2}{x-1}\right)\cdot\dfrac{\sqrt{x}+1}{\sqrt{x}}\)

\(=\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)-\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)^2\cdot\left(\sqrt{x}-1\right)}\cdot\dfrac{\sqrt{x}+1}{\sqrt{x}}\)

\(=\dfrac{x+\sqrt{x}-2-x+\sqrt{x}+2}{x-1}\cdot\dfrac{1}{\sqrt{x}}\)

\(=\dfrac{2}{x-1}\)

đề sai rồi bạn sửa lại đi rồi mình giúp

d: \(\Leftrightarrow x^3+6x^2+12x+8-x^3+6x^2-12x+8=12x^2-12x-8\)

\(\Leftrightarrow12x^2+16=12x^2-12x-8\)

=>-12x=24

hay x=-2

e: \(\left(x+5\right)\left(x+2\right)-3\left(4x-3\right)=\left(x-5\right)^2\)

\(\Leftrightarrow x^2+7x+10-12x+9=x^2-10x+25\)

=>-5x+19=-10x+25

=>5x=6

hay x=6/5

f: \(\dfrac{x-5}{100}+\dfrac{x-4}{101}+\dfrac{x-3}{102}=\dfrac{x-100}{5}+\dfrac{x-101}{4}+\dfrac{x-102}{3}\)

=>x-105=0

hay x=105