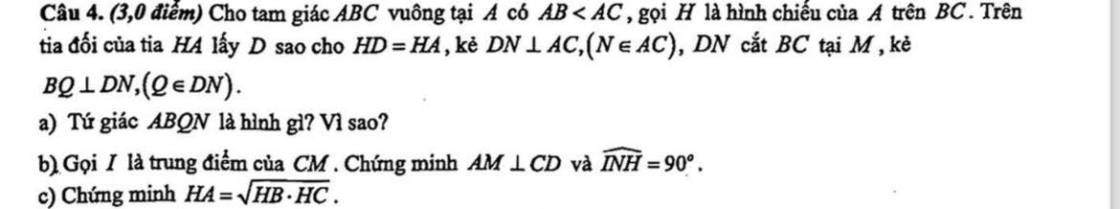Để làm dạng này , bạn làm như sau :

Vì bạn biết 1 giờ = 60 phút; 1 phút =60 giây nên là

Trước hết bạn lấy số 0,8325 (số chỉ giờ) nhân 60 nhé = 49,95

Bạn lấy phần nguyên của nó trước dấu phẩy là 49 , điền vảo chỗ chấm trước phút.

Cái phần thập phân sau dấu phẩy là 0,95 bạn tiếp tục nhân 60 = 57.

Bạn điền 57 vào phần chỗ chấm trước giây.

Vậy 0,8325 giờ=49 phút 57 giây

0,8325 giờ = 49 phút 57 giây

Đề bài đâu rồi ạ, có đề mới giải được ạ

a: Xét tứ giác ABQN có

\(\widehat{BQN}=\widehat{QNA}=\widehat{NAB}=90^0\)

=>ABQN là hình chữ nhật

b: Xét ΔCAD có

DN,CH là các đường cao

DN cắt CH tại M

Do đó: M là trực tâm của ΔCAD

=>AM\(\perp\)CD

c: Xét ΔHAB vuông tại H và ΔHCA vuông tại H có

\(\widehat{HAB}=\widehat{HCA}\left(=90^0-\widehat{ABC}\right)\)

Do đó: ΔHAB đồng dạng với ΔHCA

=>\(\dfrac{HA}{HC}=\dfrac{HB}{HA}\)

=>\(HA^2=HB\cdot HC\)

=>\(HA=\sqrt{HB\cdot HC}\)

ĐK: `x \ne kπ`

`cot(x-π/4)+cot(π/2-x)=0`

`<=>cot(x-π/4)=-cot(π/2-x)`

`<=>cot(x-π/4)=cot(x-π/2)`

`<=> x-π/4=x-π/2+kπ`

`<=>0x=-π/4+kπ` (VN)

Vậy PTVN.

hahihihihi

E tk nha:

\(1,ĐK:x\ge2\\ PT\Leftrightarrow\sqrt{3x-6}+x-2-\left(\sqrt{2x-3}-1\right)=0\\ \Leftrightarrow\dfrac{3\left(x-2\right)}{\sqrt{3x-6}}+\left(x-2\right)-\dfrac{2\left(x-2\right)}{\sqrt{2x-3}+1}=0\\ \Leftrightarrow\left(x-2\right)\left(\dfrac{3}{\sqrt{3x-6}}-\dfrac{2}{\sqrt{2x-3}+1}+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=2\left(tm\right)\\\dfrac{3}{\sqrt{3x-6}}-\dfrac{2}{\sqrt{2x-3}+1}+1=0\left(1\right)\end{matrix}\right.\)

Với \(x>2\Leftrightarrow-\dfrac{2}{\sqrt{2x-3}+1}>-\dfrac{2}{1+1}=-1\left(3x-6\ne0\right)\)

\(\Leftrightarrow\left(1\right)>0-1+1=0\left(vn\right)\)

Vậy \(x=2\)

\(2,ĐK:x\ge-1\)

Đặt \(\left\{{}\begin{matrix}\sqrt{x+1}=a\\\sqrt{x^2-x+1}=b\end{matrix}\right.\left(a,b\ge0\right)\Leftrightarrow a^2+b^2=x^2+2\)

\(PT\Leftrightarrow2a^2+2b^2-5ab=0\\ \Leftrightarrow\left(a-2b\right)\left(2a-b\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}a=2b\\b=2a\end{matrix}\right.\)

Với \(a=2b\Leftrightarrow x+1=4x^2-4x+4\left(vn\right)\)

Với \(b=2a\Leftrightarrow4x+4=x^2-x+1\Leftrightarrow x^2-5x-3=0\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5+\sqrt{37}}{2}\left(tm\right)\\x=\dfrac{5-\sqrt{37}}{2}\left(tm\right)\end{matrix}\right.\)

Vậy ...

\(3,ĐK:x\ge-1\\ PT\Leftrightarrow3\left(x^2-x+1\right)-2\left(x+1\right)=5\sqrt{x^3+1}\) 

Đặt \(\left\{{}\begin{matrix}\sqrt{x+1}=a\\\sqrt{x^2-x+1}=b\end{matrix}\right.\left(a,b\ge0\right)\)

\(PT\Leftrightarrow3b^2-2a^2=5ab\\ \Leftrightarrow2a^2+5ab-3b^2=0\\ \Leftrightarrow\left[{}\begin{matrix}a=2b\\a=-3b\left(vn\right)\end{matrix}\right.\Leftrightarrow a=2b\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5+\sqrt{37}}{2}\\x=\dfrac{5-\sqrt{37}}{2}\end{matrix}\right.\left(\text{giống bài 2}\right)\)

     2\(\sqrt{\dfrac{16}{3}}\)  - 3\(\sqrt{\dfrac{1}{27}}\) - \(\dfrac{3}{2\sqrt{3}}\)

= \(\dfrac{8}{\sqrt{3}}\) - \(\dfrac{3}{3\sqrt{3}}\)  - \(\dfrac{3}{2\sqrt{3}}\)

= \(\dfrac{8}{\sqrt{3}}\) - \(\dfrac{1}{\sqrt{3}}\) - \(\dfrac{3}{2\sqrt{3}}\)

= \(\dfrac{16}{2\sqrt{3}}\) - \(\dfrac{2}{2\sqrt{3}}\) - \(\dfrac{3}{2\sqrt{3}}\)

= \(\dfrac{11}{2\sqrt{3}}\)

= \(\dfrac{11\sqrt{3}}{6}\)

f, 2\(\sqrt{\dfrac{1}{2}}\)- \(\dfrac{2}{\sqrt{2}}\) + \(\dfrac{5}{2\sqrt{2}}\)

= \(\dfrac{2}{\sqrt{2}}\) - \(\dfrac{2}{\sqrt{2}}\) + \(\dfrac{5}{2\sqrt{2}}\)

= \(\dfrac{5}{2\sqrt{2}}\)

= \(\dfrac{5\sqrt{2}}{4}\)

(1 + \(\dfrac{3-\sqrt{3}}{\sqrt{3}-1}\)).(1- \(\dfrac{3+\sqrt{3}}{\sqrt{3}+1}\)) 

= \(\dfrac{\sqrt{3}-1+3-\sqrt{3}}{\sqrt{3}-1}\).\(\dfrac{\sqrt{3}+1-3+\sqrt{3}}{\sqrt{3}+1}\)

= \(\dfrac{2}{\sqrt{3}-1}\).\(\dfrac{-2}{\sqrt{3}+1}\)

= \(\dfrac{-4}{3-1}\)

= \(\dfrac{-4}{2}\)

= -2

   \(\dfrac{2}{\sqrt{6}-2}+\dfrac{2}{\sqrt{6}+2}+\dfrac{5}{\sqrt{6}}\)

= \(\dfrac{2.\left(\sqrt{6}+2\right)+2\left(\sqrt{6}-4\right)}{\left(\sqrt{6}-2\right)}\) + \(\dfrac{5}{\sqrt{6}}\)

= \(\dfrac{2\sqrt{6}+4+2\sqrt{6}-4}{6-4}\) + \(\dfrac{5\sqrt{6}}{6}\)

= \(\dfrac{4\sqrt{6}}{2}\) + \(\dfrac{5\sqrt{6}}{6}\)

= \(\dfrac{12\sqrt{6}+5\sqrt{6}}{6}\)

= \(\dfrac{17\sqrt{6}}{6}\)

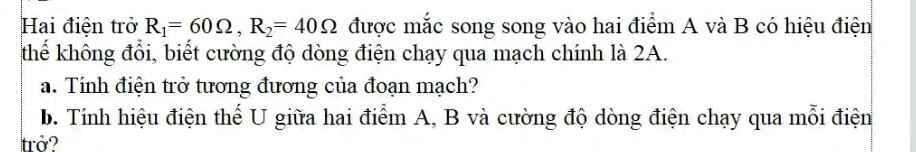
a) Điện trở tương đương của đoạn mạch :

\(R_{tđ}=\dfrac{R_1.R_2}{R_1+R_2}=\dfrac{60.40}{60+40}=24\left(\Omega\right)\)

b) Hiệu điện thế giữa hai đầu đoạn mạch :

\(U=I.R_{tđ}=2.24=48\left(V\right)\)

⇒ \(U=U_1=U_2=48\left(V\right)\) (vì R₁ // R₂)

Cường độ dòng điện chạy qua mỗi điện trở :

\(I_1=\dfrac{U_1}{R_1}=\dfrac{48}{60}=0,8\left(A\right)\)

\(I_2=\dfrac{U_2}{R_2}=\dfrac{48}{40}=1,2\left(A\right)\)

 Chúc bạn học tốt