Chọn A

Pt <=> 2sin\(\dfrac{3x}{2}\).cos\(\dfrac{x}{2}\) = 2cos\(\dfrac{3x}{2}\).cos\(\dfrac{x}{2}\)

⇔ cos\(\dfrac{x}{2}\) . \(\left(sin\dfrac{3x}{2}-cos\dfrac{3x}{2}\right)\) = 0

⇔ \(\sqrt{2}sin\left(\dfrac{3x}{2}-\dfrac{\pi}{4}\right).cos\dfrac{x}{2}=0\)

⇔ 

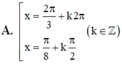
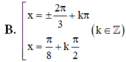
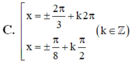
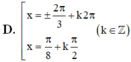
Chọn D

Ta sẽ biến đổi phương trình thành dạng tích

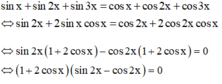
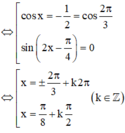
Chú ý: có thể dùng 4 đáp án thay vào phương trình để kiểm tra đâu là nghiệm

\(\sqrt{3}cos2x-sin2x=\sqrt{3}sinx+cosx\)

\(\Leftrightarrow\sqrt{3}cos2x-\sqrt{3}sinx-sin2x-cosx=0\)

\(\Leftrightarrow\sqrt{3}\left(1-2sin^2x-sinx\right)-2sinx.cosx-cosx=0\)

\(\Leftrightarrow-\sqrt{3}\left(sinx+1\right)\left(2sinx-1\right)-cosx\left(2sinx-1\right)=0\)

\(\Leftrightarrow\left(2sinx-1\right)\left[\sqrt{3}\left(sinx+1\right)+cosx\right]=0\)

\(\Leftrightarrow\left(2sinx-1\right)\left(\sqrt{3}sinx+cosx+\sqrt{3}\right)=0\)

\(\Leftrightarrow sinx=\dfrac{1}{2}\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k2\pi\\x=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)

`cos 2x+\sqrt{3}sin 2x+\sqrt{3}sin x-cos x=4`

`<=>1/2 cos 2x+\sqrt{3}/2 sin 2x+\sqrt{3}/2 sin x-1/2 cos x=2`

`<=>sin(\pi/6 +2x)+sin(x-\pi/6)=2`

Vì `-1 <= sin (\pi/6 +2x) <= 1`

     `-1 <= sin (x-\pi/6) <= 1`

 Dấu "`=`" xảy ra `<=>{(sin(\pi/6+2x)=1),(sin(x-\pi/6)=1):}`

        `<=>{(\pi/6+2x=\pi/2+k2\pi),(x-\pi/6=\pi/2+k2\pi):}`

        `<=>{(x=\pi/6+k\pi),(x=[2\pi]/3+k2\pi):}`    `(k in ZZ)`

ĐK: \(x\ne\dfrac{\pi}{4}+k\pi;x\ne\dfrac{k\pi}{2}\)

\(\dfrac{2sin^2x+cos4x-cos2x}{\left(sinx-cosx\right)sin2x}=0\)

\(\Leftrightarrow2sin^2x+cos4x-cos2x=0\)

\(\Leftrightarrow2sin^2x-1+cos4x-cos2x+1=0\)

\(\Leftrightarrow2cos^22x-2cos2x=0\)

\(\Leftrightarrow\left[{}\begin{matrix}cos2x=0\\cos2x=1\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}2x=\dfrac{\pi}{2}+k\pi\\2x=k2\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+\dfrac{k\pi}{2}\\x=k\pi\end{matrix}\right.\)

Đối chiếu điều kiện ta được \(x=-\dfrac{\pi}{4}+k\pi\)

    1 + sinx + cosx + sin2x + cos2x = 0

<=> sin^2x+ cos^2 x + ( sinx+cosx) + 2.sinx.cosx + ( cos^2 x - sin^2 x)=0

<=> 2 cos^2 x + 2sinx.cosx + sinx + cosx =0

<=> 2cosx ( cos x + sinx) + sinx + cosx = 0

<=> ( cosx + sinx ) (2 cos x + 1 ) = 0

<=> cosx + sinx = 0 hoặc 2cosx + 1 =0

Đáp án A

Ta có: