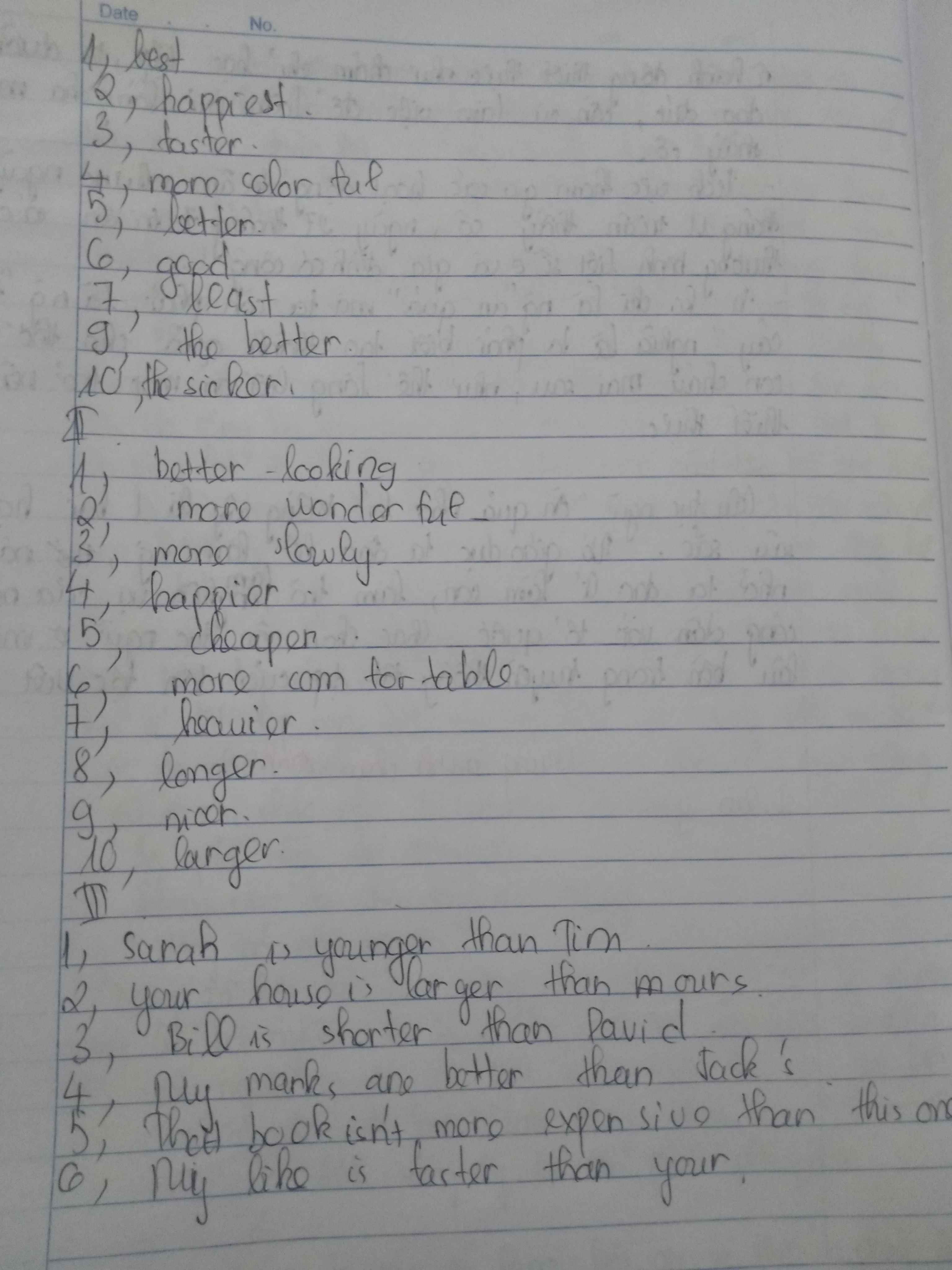giúpp
giúpp

Những câu hỏi liên quan
giúpp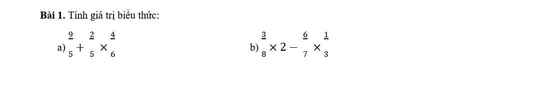
a) 9/5 + 2/5 x 4/6 = 9/5 + 4/15 = 27/15 + 4/15 = 31/15
b) 3/8 x 2 - 6/7 x 1/3 = 3/4 - 2/7 = 21/28 - 8/28 = 13/28
Đúng 0
Bình luận (0)
a) 9/5 + 2/5 x 4/6 = 9/5 + 4/15 = 27/15 + 4/15 = 31/15
b) 3/8 x 2 - 6/7 x 1/3 = 3/4 - 2/7 = 21/28 - 8/28 = 13/28
Đúng 0
Bình luận (0)



giúpp
1. It is easy for everyone to get access to the Internet
2.Solar
Đúng 0
Bình luận (0)
1 not
2 It is easy for everyone to get access to the internet
3 C
Đúng 0
Bình luận (0)
giúpp tui
I,
1. best
2. happiest
3. faster
4. more colourful
5. better
6. good
7. least
8. prettiest
9. the best
10. the sicker
Đúng 2
Bình luận (0)
I/
1. best
2. happiest
3. faster
4. more colourful
5. better
6. good
7. least
8. prettier
9. the better
10. the sticker
II/
3. more slowly
III/
1. Sarah is younger than Tim
2. Your house is smaller than ours
3. Bill is shorter than David
4. My marks are better than Jack's
5. That book is as expensive as this one
6. My bike is faster than yours
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
giúpp với
Đọc tiếp

 giúpp với
giúpp với
Giúpp emm 

Giúpp em vớiii😿
4:
Gọi số xe loại 45 chỗ và 16 chỗ lần lượt là a,b
Có tổng cộng là 9 xe nên a+b=9
Có 289 người tham gia nên 45a+16b=289
Do đó, ta có hệ:
a+b=9 và 45a+16b=289
=>a=5 và b=4
5:
a: Số tiền vốn là:
300000*100=30000000(đồng)
Số tiền thu về là:
30000000+12300000=42300000(đồng)
b; Gọi số tiền cửa hàng bán 1 chiếc áo vào thời điểm khuyến mãi là x
=>Số tiền vốn là x:0,7=10/7x
Theo đề, ta có:
10/7x*80+x*20=42300000
=>x=315000
Đúng 0
Bình luận (0)
 Giúpp e với ạaa
Giúpp e với ạaa
a. Em tự giải
b.
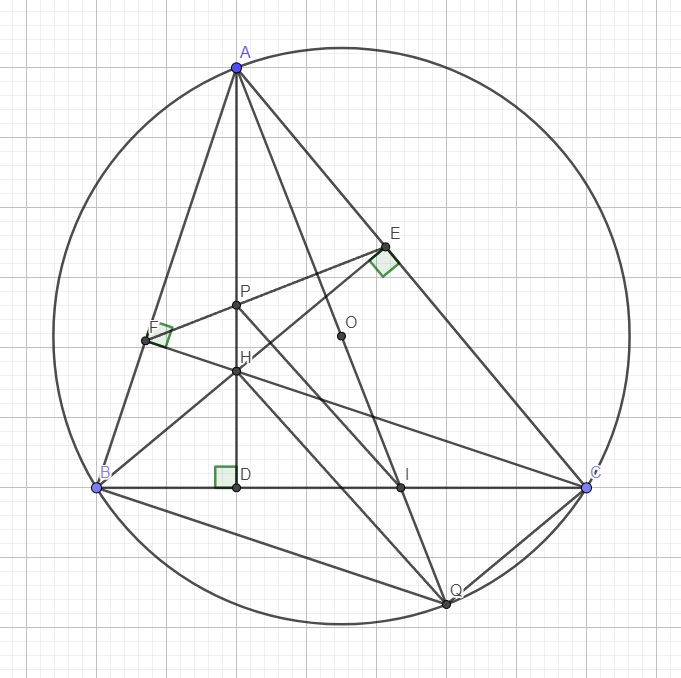
Ta có: \(\widehat{ABC}=\widehat{AQC}\) (cùng chắn AC) (1)
Do AQ là đường kính \(\Rightarrow\widehat{ACQ}\) là góc nt chắn nửa đường tròn
\(\Rightarrow\widehat{ACQ}=90^0\) \(\Rightarrow\widehat{ACQ}+\widehat{CAQ}=90^0\) (2)
Tam giác ABD vuông tại D \(\Rightarrow\widehat{BAD}+\widehat{ABC}=90^0\) (3)
(1);(2);(3) \(\Rightarrow\widehat{CAQ}=\widehat{BAD}\)
c.
\(\left\{{}\begin{matrix}\widehat{PAE}=\widehat{PAI}+\widehat{CAQ}\\\widehat{IAB}=\widehat{PAI}+\widehat{BAD}\\\widehat{CAQ}=\widehat{BAD}\left(cmt\right)\end{matrix}\right.\) \(\Rightarrow\widehat{PAE}=\widehat{IAB}\) (3)
Tứ giác BCEF nội tiếp (E và F cùng nhìn BC dưới 1 góc vuông)
\(\Rightarrow\widehat{ABI}+\widehat{CEF}=180^0\)
Mà \(\widehat{CEF}+\widehat{AEP}=180^0\)
\(\Rightarrow\widehat{AEP}=\widehat{ABI}\) (4)
(3);(4) \(\Rightarrow\Delta AEP\sim\Delta ABI\left(g.g\right)\)
\(\Rightarrow\dfrac{AP}{AI}=\dfrac{AE}{AB}\) (5)
AQ là đường kính \(\Rightarrow\widehat{ABQ}\) là góc nt chắn nửa đường tròn \(\Rightarrow\widehat{ABQ}=90^0\)
Xét 2 tam giác ABQ và AEH có: \(\left\{{}\begin{matrix}\widehat{ABQ}=\widehat{AEH}=90^0\\\widehat{BAQ}=\widehat{EAH}\left(\text{theo (3)}\right)\end{matrix}\right.\) \(\Rightarrow\Delta ABQ\sim\Delta AEH\left(g.g\right)\)
\(\Rightarrow\dfrac{AE}{AB}=\dfrac{AH}{AQ}\) (6)
(5);(6) \(\Rightarrow\dfrac{AH}{AQ}=\dfrac{AP}{AI}\) \(\Rightarrow\dfrac{AP}{AH}=\dfrac{AI}{AQ}\)
\(\Rightarrow PI||HQ\) (định lý Talet đảo)
Đúng 2
Bình luận (0)
Mọi ng giúpp mih với