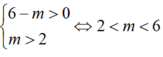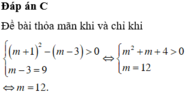tìm tất cả các giá trị thực của mm để phương trình 9x - 4.3x +m-2=0 có 2 nghiệm phân biệt

Những câu hỏi liên quan
Tổng tất cả các giá trị nguyên của tham số m để phương trình
9
x
-
4
.
3
x
+
m
-
2
0
có hai nghiệm thực phân biệt. A. 2019 B. 15 C. 12 D. 2018
Đọc tiếp
Tổng tất cả các giá trị nguyên của tham số m để phương trình 9 x - 4 . 3 x + m - 2 = 0 có hai nghiệm thực phân biệt.
A. 2019
B. 15
C. 12
D. 2018
Cho phương trình
9
x
−
2
m
+
1
3
x
+
m
−
3
0
.
Tìm tất cả giá trị thực của tham số m để phương trình có hai nghiệm phân biệt
x
1
,
x
2
sao cho
x
1...
Đọc tiếp
Cho phương trình 9 x − 2 m + 1 3 x + m − 3 = 0 . Tìm tất cả giá trị thực của tham số m để phương trình có hai nghiệm phân biệt x 1 , x 2 sao cho x 1 + x 2 = 2 .
A. m = 1
B. m = 1 2
C. m = 12
D. m = 3 2
Tìm tất cả các giá trị thực của m để phương trình \(4^x-2^{x+1}+m=0\) có 2 nghiệm thực phân biệt
Đặt \(t=2^x>0\).
Phương trình ban đầu trở thành: \(t^2-2t+m=0\) (*)
Để phương trình ban đầu có 2 nghiệm phân biệt thì (*) phải có 2 nghiệm phân biệt dương: \(\left\{{}\begin{matrix}\Delta'>0\\t_1+t_2>0\\t_1t_2>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}1-m>0\\2>0\left(đúng\right)\\m>0\end{matrix}\right.\Leftrightarrow0< m< 1\)
Đúng 1
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m để phương trình
4
x
−
2
m
.2
x
+
m
+
2
0
có 2 nghiệm phân biệt. A.
−
2
m
2
B.
m
−
2
C. m 2 D. m 2
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để phương trình 4 x − 2 m .2 x + m + 2 = 0 có 2 nghiệm phân biệt.
A. − 2 < m < 2
B. m > − 2
C. m > 2
D. m < 2
Đáp án C
Phương pháp:
Đặt 2 x = t t > 0 , đưa về phương trình bậc 2 ẩn t, tìm điều kiện của phương trình bậc 2 ẩn t để phương trình ban đầu có 2 nghiệm phân biệt.
Cách giải: Đặt 2 x = t t > 0 khi đó phương trình trở thành t 2 − 2 m t + m + 2 = 0 *
Để phương trình ban đầu có 2 nghiệm phân biệt thì phương trình (*) có 2 nghiệm dương phân biệt.
Khi đó: Δ ' > 0 S > 0 P > 0 ⇔ m 2 − m − 2 > 0 2 m > 0 m + 2 > 0 ⇔ m > 2 m < − 1 m > 0 m > − 2 ⇒ m > 2
Chú ý và sai lầm: Rất nhiều học sinh sau khi đặt ẩn phụ thì quên mất điều kiện t > 0, dẫn đến việc chỉ đi tìm điều kiện đề phương trình (*) có 2 nghiệm phân biệt.
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị của tham số m để phương trình
9
x
−
2
m
+
1
3
x
+
m
+
1
0
có hai nghiệm phân biệt. A.
m
3
2
B.
m
−
3...
Đọc tiếp
Tìm tất cả các giá trị của tham số m để phương trình 9 x − 2 m + 1 3 x + m + 1 = 0 có hai nghiệm phân biệt.
A. m > 3 2
B. m < − 3 2
C. m > − 1 2
D. m > − 1
tìm tất cả các giá trị thực của tham số m để phương trình x-4√(x+3 ) + m = 0 có 2 nghiệm phân biệt
\(x-4\sqrt{x+3}+m=0\)
\(\Leftrightarrow x+3-4\sqrt{x+3}-3+m=0\left(1\right)\)
\(đăt:\sqrt{x+3}=t\left(t\ge0\right)\)
\(\left(1\right)\Leftrightarrow t^2-4t-3+m=0\Leftrightarrow f\left(t\right)=t^2-4t-3=-m\left(2\right)\)
\(\left(1\right)-có-2ngo-phân-biệt\Leftrightarrow\left(2\right)có-2ngo-phân-biệt-thỏa:t\ge0\)
\(\Rightarrow f\left(0\right)=-3\)
\(\Rightarrow f\left(t\right)min=\dfrac{-\Delta}{4a}=-7\Leftrightarrow t=2\)
\(\Rightarrow-7< -m\le-3\Leftrightarrow3\le m< 7\)
Đúng 2
Bình luận (2)
Tìm tất cả các giá trị thực của tham số m để phương trình ( m2 - 4 ) x4 + ( m - 2 ) x 2 + 1 = 0. Có đúng hai nghiệm phân biệt.!!
Trường hợp 1: \(m\ne\pm2\)
Để phương trình có đúng hai nghiệm phân biệt thì phương trình này sẽ có hai nghiệm trái dấu
=>\(m^2-4< 0\)
hay -2<m<2
Trường hợp 2: m=2
Pt sẽ là 1=0(vô lý)
Trường hợp 3: m=-2
=>-4x2+1=0(nhận)
Vậy: -2<=m<2
Đúng 1
Bình luận (1)
Tìm tất cả các giá trị thực của tham số m để phương trình \(x^2-3mx+m+1=0\)
có hai nghiệm phân biệt và
một nghiệm gấp đôi nghiệm còn lại.
Cho phương trình
4
x
2
-
2
x
+
1
-
m
.
2
x
2
-
2
x
+
2
+
3
m
-
2
0...
Đọc tiếp
Cho phương trình 4 x 2 - 2 x + 1 - m . 2 x 2 - 2 x + 2 + 3 m - 2 = 0 với m là tham số thực. Tìm tất cả các giá trị của m để phương trình có bốn nghiệm phân biệt.
A. m < 1
B. m < 1; m > 2
C. m ≥ 2
D. m > 2