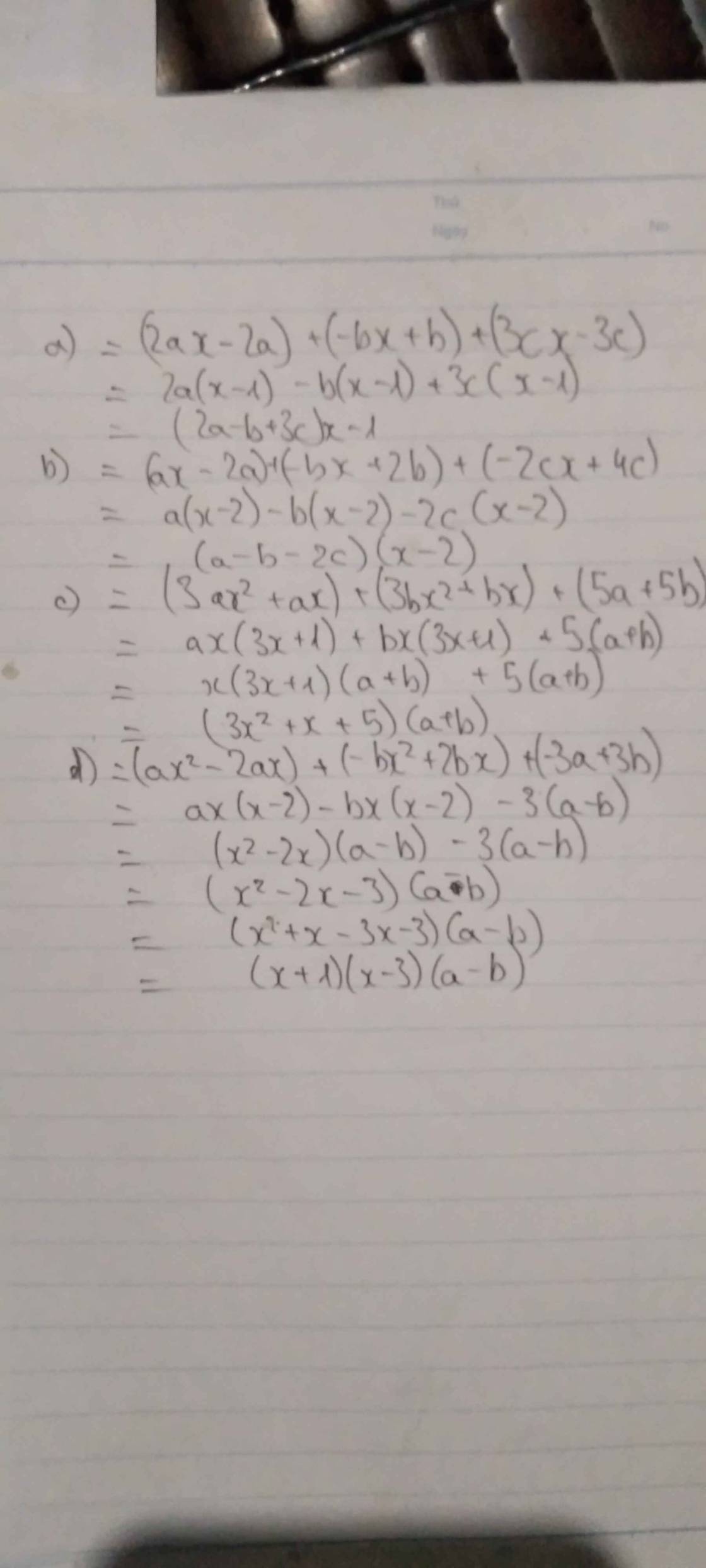phân tích thành nhân tử
ax^2+bx^2-bx-ax+a+b

Những câu hỏi liên quan
Phân tích đa thức thành nhân tử
ax2 - ax + bx2 -bx + a + b
ax2 - ax + bx2 -bx + a + b
= (ax2+ bx2 ) - (ax + bx) + (a + b)
=x2 (a + b) - x(a + b) + (a + b)
= (x2 - x + 1)(a + b)
ax2 - ax + bx2 - bx + a + b
= ( ax2 + bx2 ) - ( ax + bx ) + ( a + b )
= x2( a + b ) - x( a + b ) + ( a + b )
= ( a + b )( x2 - x + 1 )
\(ax^2-ax+bx^2-bx+a+b\)
\(=ax\left(x-1\right)+bx\left(x-1\right)+\left(a+b\right)\)
\(=x\left(x-1\right)\left(a+b\right)+\left(a+b\right)\)
\(=\left(a+b\right)\left(x^2-x+1\right)\)
Xem thêm câu trả lời
Phân tích thành nhân tử (mọi người làm chi tiết ạ)
\(2ax-bx+3cx-2a+b-3c\)
\(ax-bx-2cx-2a+2b+4c\)
\(3ax^2 +3bx^2 +ax+bx+5a+5b\)
\(ax^2 -bx^2 -2ax+2bx-3a+3b\)
\(2ax-bx+3cx-2a+b-3c\\ =x\left(2a-b+3c\right)-\left(2a-b+3c\right)\\ =\left(x-1\right)\left(2a-b+3c\right)\)
\(ax-bx-2cx-2a+2b+4c\\ =x\left(a-b-2c\right)-2\left(a-b-2c\right)\\ =\left(x-2\right)\left(a-b-2c\right)\)
\(3ax^2+3bx^2+ax+bx+5a+5b\\ =3x^2\left(a+b\right)+x\left(a+b\right)+5\left(a+b\right)\\ =\left(3x^2+x+5\right)\left(a+b\right)\)
\(ax^2-bx^2-2ax+2bx-3a+3b\\ =x^2\left(a-b\right)-2x\left(a-b\right)-3\left(a+b\right)\\ =\left(x^2-2x-3\right)\left(a+b\right)\\ =\left(x+1\right)\left(x-3\right)\left(a+b\right)\)
Đúng 1
Bình luận (0)
phân tích đa thúc thành nhân tử: ax -bx -a^2 +2ab -b^2
\(=x\left(a-b\right)-\left(a^2-2ab+b^2\right)=\)
\(=\left(a-b\right)x-\left(a-b\right)^2=\)
\(=\left(a-b\right)\left[x-\left(a-b\right)\right]=\left(a-b\right)\left(x-a+b\right)\)
Đúng 1
Bình luận (0)
Phân tích các đa thức sau thành nhân tử
ax^2 + bx^2 - bx - ax + cx^2 - cx
\(ax^2+bx^2-bx-ax+cx^2-cx\)
\(=\left(ax^2-ax\right)+\left(bx^2-bx\right)+\left(cx^2-cx\right)\)
\(=ax\left(x-1\right)+bx\left(x-1\right)+cx\left(x-1\right)\)
\(=\left(x-1\right)\left(ax+bx+cx\right)\)
\(=x\left(x-1\right)\left(a+b+c\right)\)
ax2+bx2-bx-ax+cx2-cx
= (ax2 - ax ) + (bx2 -bx ) + ( cx2 - cx )
= a(x) + b(x) + c(x)
= (x)(a+b+c)
Phân tích đa thức thành nhân tử:
a)A=4acx+4bcx+4x+4bx
b)B=ax-bx+cx-3a+3b-3c
c)C=2ax-bx+3cx-2a+b-3c
d)D=ax-bx-2cx-2a+2b+4c
e)E=3ax2+3bx2+ax+bx+5a+5b
f)F=ax2-bx2-2ax+2bx-3a+3b
A = 4acx + 4bcx + 4ax + 4bx ( đã sửa '-' )
= 4x( ac + bc + a + b )
= 4x[ c( a + b ) + ( a + b ) ]
= 4x( a + b )( c + 1 )
B = ax - bx + cx - 3a + 3b - 3c
= x( a - b + c ) - 3( a - b + c )
= ( a - b + c )( x - 3 )
C = 2ax - bx + 3cx - 2a + b - 3c
= x( 2a - b + 3c ) - ( 2a - b + 3c )
= ( 2a - b + 3c )( x - 1 )
D = ax - bx - 2cx - 2a + 2b + 4c
= x( a - b - 2c ) - 2( a - b - 2c )
= ( a - b - 2c )( x - 2 )
E = 3ax2 + 3bx2 + ax + bx + 5a + 5b
= 3x2( a + b ) + x( a + b ) + 5( a + b )
= ( a + b )( 3x2 + x + 5 )
F = ax2 - bx2 - 2ax + 2bx - 3a + 3b
= x2( a - b ) - 2x( a - b ) - 3( a - b )
= ( a - b )( x2 - 2x - 3 )
= ( a - b )( x2 + x - 3x - 3 )
= ( a - b )[ x( x + 1 ) - 3( x + 1 ) ]
= ( a - b )( x + 1 )( x - 3 )
Phân tích đa thức dau thành nhân tử
a)x^2+2x-4y^2-4y
b)x^4-6x^3+54x-81
c)ax^2+ax-bx^2-bx-a+b
d)(x^2+y^2-2)-(2xy-2)^2
a)x^2+2x-4y^2-4y
=(x2-4y2)+(2x-4y)
=(x-2y)(x+2y)+2.(x-2y)
=(x-2y)(x+2y+2)
b)x^4-6x^3+54x-81
=(x4-81)+(-6x3+54x)
=(x2-9)(x2+9)-6x.(x2-9)
=(x2-9)(x2+9-6x)
=(x-3)(x+3)(x-3)2
=(x-3)3(x+3)
c)ax^2+ax-bx^2-bx-a+b
=(ax2-bx2)+(ax-bx)+(-a+b)
=x2.(a-b)+x.(a-b)-(a-b)
=(a-b)(x2+x+1)
Đúng 0
Bình luận (0)
Phân tích đa thức thành nhân tử( Nhóm các hạng tử)
a) xy+1-x-y
b) x^2+ab+ac+bx
c)ax+bx-cx+a+b-c
a ) xy + 1 - x - y
= x ( y - 1 ) + 1 - y
= x ( y - 1 ) - ( y - 1 )
= ( x - 1 ) ( y - 1 )
b ) x2 + ab + ac + bx
= ( b + x )x + a( b + c )
= ( b + x )1x + 1a( b + c )
= ( b + x ) ( x + a ) ( b + c )
c ) ax + bx - cx + a + b - c
= ( a + b - c )x + a + b - c
= ( a + b - c )x + ( a + b - c )1
= ( a + b - c ) ( x + 1 )
Bài 2 : Phân tích các đa thức sau thành nhân tử :
a) x2 - ( m + n )x + mn
b) ax + by + a - bx - ay - b
\(a,=x^2-mx-nx+mn=x\left(x-m\right)-n\left(x-m\right)=\left(x-n\right)\left(x-m\right)\\ b,=a\left(x-y\right)-b\left(x-y\right)+\left(a-b\right)\\ =\left(x-y\right)\left(a-b\right)+\left(a-b\right)=\left(a-b\right)\left(x-y+1\right)\)
Đúng 0
Bình luận (0)
b: \(=a\left(x-y\right)-b\left(x-y\right)+a-b\)
\(=\left(x-y+1\right)\left(a-b\right)\)
Đúng 0
Bình luận (0)
a) \(x^2-\left(m+n\right)x+mn=\left(x^2-n\cdot x\right)-\left(m\cdot x-m\cdot n\right)=x\left(x-n\right)-m\left(x-n\right)=\left(x-m\right)\left(x-n\right)\)
b) \(ax+by+a-bx-ay-b\)
\(=\left(ax-ay+a\right)-\left(bx-by+b\right)\)
\(=a\left(x-y+1\right)-b\left(x-y+1\right)\)
\(\left(a-b\right)\left(x-y+1\right)\)
Đúng 0
Bình luận (0)
Phân tích thành nhân tử (mọi người làm chi tiết ạ)
\(ax^2 -3axy+bx-3by\)
\(5x^2 y+5xy^2 -a^2 x-a^2 y\)
\(2ax^3 +6ax^2 +6ax+18a\)
\(10xy^2 -5by^2 +2ax-ab\)
\(ax-bx+cx-3a+3b-3c\)
\(ax^2-3axy+bx-3by\\ =x\left(ax+b\right)-3y\left(ax+b\right)\\ =\left(x-3y\right)\left(ax+b\right)\)
\(5x^2y+5xy^2-a^2x-a^2y\\ =5xy\left(x+y\right)-a^2\left(x+y\right)\\ =\left(5xy-a^2\right)\left(x+y\right)\)
\(2ax^3+6ax^2+6ax+18a\\ =2ax^2\left(x+3\right)+6a\left(x+3\right)\\ =2a\left(x^2+3\right)\left(x+3\right)\)
\(10xy^2-5by^2+2ax-ab\\ =5y^2\left(2x-b\right)+a\left(2x-b\right)\\ =\left(5y^2+a\right)\left(2x-b\right)\)
\(ax-bx+cx-3a+3b-3c\\ =x\left(a-b+c\right)-3\left(a-b+c\right)\\ =\left(x-3\right)\left(a-b+c\right)\)
Đúng 1
Bình luận (1)
Chứng tỏ rằng nếu phương trình ax2 + bx + c = 0 có nghiệm là x1 và x2 thì tam thức ax2 + bx + c phân tích được thành nhân tử như sau: ax2 + bx +c = a(x - x1)(x - x2).
Áp dụng: Phân tích đa thức thành nhân tử:
a) 2x2 - 5x + 3; b) 3x2 + 8x + 2.
a) Phương trình 2x2 – 5x + 3 = 0 có a + b + c = 2 – 5 + 3 = 0 nên có hai nghiệm là x1 = 1, x2 = \(\dfrac{3}{2}\) nên:
2x2 – 5x + 3 = 2(x – 1)(x2 - \(\dfrac{3}{2}\)) = (x – 1)(2x – 3)
b) Phương trình 3x2 + 8x + 2 có a = 3, b = 8, b’ = 4, c = 2.
Nên ∆’ = 42 – 3 . 2 = 10, có hai nghiệm là:
x1 = \(\dfrac{-4-\sqrt{10}}{3}\), x2 = \(\dfrac{-4+\sqrt{10}}{3}\)
nên: 3x2 + 8x + 2 = 3(x - \(\dfrac{-4-\sqrt{10}}{3}\))(x - \(\dfrac{-4+\sqrt{10}}{3}\))
= 3(x + \(\dfrac{4+\sqrt{10}}{3}\))(x + \(\dfrac{4-\sqrt{10}}{3}\))
Đúng 0
Bình luận (0)
a,) Phương trình 2x2 – 5x + 3 = 0 có a + b + c = 2 – 5 + 3 = 0 nên có hai nghiệm là x1 = 1, x2=\(\dfrac{3}{2}\) nên:
2x2 – 5x + 3 = 2(x – 1)(x2 -\(\dfrac{3}{2}\) ) = (x – 1)(2x – 3)
b) Phương trình 3x2 + 8x + 2 có a = 3, b = 8, b’ = 4, c = 2.
Nên ∆’ = 42 – 3 . 2 = 10, có hai nghiệm là:
x1 =\(\dfrac{-4-\sqrt{10}}{3}\) , x2 =\(\dfrac{-4+\sqrt{10}}{3}\)
nên: 3x2 + 8x + 2 = 3(x - \(\dfrac{4+\sqrt{10}}{3}\) )(x -\(\dfrac{4-\sqrt{10}}{3}\) )
= 3(x + )(x + )
Đúng 0
Bình luận (0)