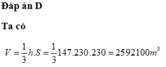weo, lịch sử lớp 5

Tham khảo

Được biết là dãy số “142857” được phát hiện bên trong kim tự tháp Ai Cập, điều này chứng minh rằng một tuần có 7 ngày, là sự kết hợp của bội số tăng dần, 6 chữ số này luân phiên xuất hiện một lần và nghỉ vào ngày thứ 7 để dãy số 999999 thay thế, bội số tiếp tục tăng dần, mỗi khi qua một tuần, con số cuối cùng sẽ phải ...

hình chóp có đáy là hình vuông với bốn mặt bên là tam giác đều.

xây kim tự tháp bằng cách xây kim tự tháp

Mình đọc 7 Kỳ Quan Thế Giới rồi nhưng không nhớ (và cái đấy liên quan gì đến lịch sử lớp 4 hả bạn?)

nguyễn hà vy ơi bạn xàm quá a~ để mik trả lời cho mà nghe : để vận chuyển những khối đá lớn xây dựng kim tự tháp Giza , người Ai Cập Cổ Đại Đã biết lợi dụng sức nước , lực đẩy của nước. Ngoài việc dùng thuyền gỗ, người xưa còn sử dụng da dê và dây thừng làm thành phao nâng kéo các khối đá 

kết thúc câu trả lời ... nói tóm gọn lại là như thế đó :)))

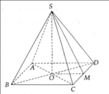
Kim tự tháp có dạng hình chóp tứ giác đều S.ABCD.

Gọi M là trung điểm của cạnh CD; O là tâm của đáy ABCD.

Tính được:

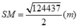
Diện tích xung quanh của kim tự tháp là:

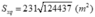
Thể tích của kim tự tháp:

V = 2436819 (m³)

Để tính cạnh bên và diện tích một mặt bên của kim tự tháp Kê-ốp, chúng ta cần sử dụng các tính chất của hình chóp tứ giác đều.

1. **Tính cạnh bên**:
   Trong một hình chóp tứ giác đều, cạnh bên có thể tính được bằng cách sử dụng định lý Pythagoras trên một tam giác vuông có cạnh góc vuông là nửa đường chéo của đáy (đường chéo chia đáy thành hai phần bằng nhau), độ dài một cạnh của đáy và chiều cao của hình chóp.

   Trong trường hợp này, nửa đường chéo của đáy là \( \frac{231}{2} = 115.5 \) m, chiều cao của hình chóp là 137 m. Ta sẽ tính độ dài cạnh bên như sau:

   \[ \text{Cạnh bên} = \sqrt{{\text{đường chéo}^2 + \text{chiều cao}^2}} \]

   \[ \text{Cạnh bên} = \sqrt{{115.5^2 + 137^2}} \]

   \[ \text{Cạnh bên} ≈ \sqrt{{13340.25 + 18769}} \]

   \[ \text{Cạnh bên} ≈ \sqrt{{32109.25}} \]

   \[ \text{Cạnh bên} ≈ 179.25 \, \text{m} \]

2. **Tính diện tích một mặt bên**:
   Diện tích một mặt bên của hình chóp tứ giác đều được tính bằng công thức:

   \[ \text{Diện tích một mặt bên} = \frac{{\text{cạnh đáy} \times \text{chiều cao}}}{{2}} \]

   Trong trường hợp này, cạnh đáy là 231 m và chiều cao là 137 m. Ta sẽ tính diện tích một mặt bên như sau:

   \[ \text{Diện tích một mặt bên} = \frac{{231 \times 137}}{{2}} \]

   \[ \text{Diện tích một mặt bên} = \frac{{31647}}{{2}} \]

   \[ \text{Diện tích một mặt bên} = 15823.5 \, \text{m}^2 \]

Vậy, cạnh bên của kim tự tháp Kê-ốp là khoảng 179.25 m và diện tích của một mặt bên là khoảng 15823.5 \( \text{m}^2 \).

Đápn án D

Ta có V = 1 3 h . S = 1 3 147 . 230 . 230 = 25921 m 3   

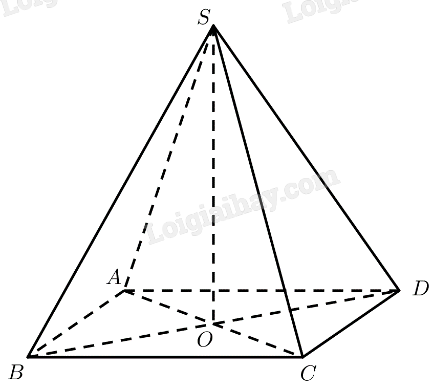
Mô hình hoá hình ảnh kim tự tháp bằng hình chóp tứ giác đều \(S.ABC{\rm{D}}\) có \(O\) là tâm của đáy. Kẻ \(SI \bot C{\rm{D}}\left( {I \in C{\rm{D}}} \right)\).

Ta có: \(SO = 136,CD = 152\)

Tam giác \(SCD\) cân tại \(S\)

\( \Rightarrow SI\) vừa là trung tuyến, vừa là đường cao của tam giác

\( \Rightarrow I\) là trung điểm của \(CD\).

Mà \(O\) là trung điểm của \(AD\)

\( \Rightarrow OI\) là đường trung bình của tam giác \(ACD\)

\( \Rightarrow OI = \frac{1}{2}BC = 76\)

\(SO \bot \left( {ABCD} \right) \Rightarrow SO \bot OI\)

\( \Rightarrow \Delta SOI\) vuông tại \(O\)

\( \Rightarrow SI = \sqrt {S{O^2} + O{I^2}}  = 4\sqrt {1517}  \approx 155,8\)

Vậy độ dài đường cao của mặt bên xuất phát từ đỉnh của kim tự tháp khoảng 155,8 m.