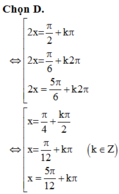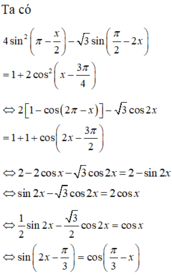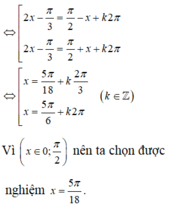Tìm nghiệm lớn nhất của phương trình \(2cos2x-1=0\) trong đoạn \(\left[0;\pi\right]\) ?

Những câu hỏi liên quan
cho phương trình \(2cos2x+sin^2xcosx+sinxcos^2x=m\left(sinx+cosx\right)\)tìm m để phương trình có ít nhất 1 nghiệm thuộc đoạn\(\left[0;\dfrac{\Pi}{2}\right]\)
\(\Leftrightarrow2\left(cos^2x-sin^2x\right)+sinx.cosx\left(sinx+cosx\right)=m\left(sinx+cosx\right)\)
\(\Leftrightarrow\left(2cosx-2sinx\right)\left(sinx+cosx\right)+sinx.cosx\left(sinx+cosx\right)=m\left(sinx+cosx\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx+cosx=0\left(\text{vô nghiệm trên đoạn xét}\right)\\2cosx-2sinx+sinx.cosx=m\left(1\right)\end{matrix}\right.\)
Xét (1), đặt \(t=cosx-sinx=\sqrt{2}cos\left(x+\dfrac{\pi}{4}\right)\)
\(\Rightarrow\left\{{}\begin{matrix}t\in\left[-1;1\right]\\sinx.cosx=\dfrac{1-t^2}{2}\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow2t+\dfrac{1-t^2}{2}=m\)
Xét hàm \(f\left(t\right)=-\dfrac{1}{2}t^2+2t+\dfrac{1}{2}\) trên \(\left[-1;1\right]\)
\(-\dfrac{b}{2a}=2\notin\left[-1;1\right]\) ; \(f\left(-1\right)=-2\) ; \(f\left(1\right)=2\)
\(\Rightarrow-2\le f\left(t\right)\le2\Rightarrow-2\le m\le2\)
Đúng 0
Bình luận (0)
Tổng các nghiệm của phương trình
sin
4
x
2
cos
2
x
-
1
trên đoạn
0
;
π
A.
7
π
4
B.
π
C.
5
π
4
D....
Đọc tiếp
Tổng các nghiệm của phương trình sin 4 x = 2 cos 2 x - 1 trên đoạn 0 ; π
A. 7 π 4
B. π
C. 5 π 4
D. 3 π 2
Tìm nghiệm của phương trình
sin
2
x
+
2
cos
2
x
+
4
cos
x
−
sin
x
−
1
0
. A.
x
±
π
3
+
k
π
B.
x
±
π
3
+
k
2
π
C.
x...
Đọc tiếp
Tìm nghiệm của phương trình sin 2 x + 2 cos 2 x + 4 cos x − sin x − 1 = 0 .
A. x = ± π 3 + k π
B. x = ± π 3 + k 2 π
C. x = ± π 6 + k π
D. x = ± π 6 + k 2 π
Phương trình \(\left(2cos2x-\pi\right)\left(sinx-cosx\right)=0\) có số nghiệm thuộc đoạn \(\left[-\pi;\pi\right]\) là
A. 4
B. 5
C. 3
D. 2
=>2cos2x=pi(loại) hoặc sin x-cosx=0
=>sin x-cosx=0
=>sin(x-pi/4)=0
=>x-pi/4=kpi
=>x=kpi+pi/4
mà x\(\in\left[-pi;pi\right]\)
nên \(x\in\left\{\dfrac{pi}{4};-\dfrac{3}{4}pi\right\}\)
=> D
Đúng 0
Bình luận (1)
Tính tổng S các nghiệm của phương trình \(\left(2cos2x+5\right)\left(sin^4x-cos^4x\right)+3=0\) trong khoảng \(\left(0;2\pi\right)\)
Phương trình
2
cos
2
x
-
1
0
có số nghiệm trên đoạn
-
2
π
;
2
π
là: A. 2. B. 4. C. 6. D. 8.
Đọc tiếp
Phương trình 2 cos 2 x - 1 = 0 có số nghiệm trên đoạn - 2 π ; 2 π là:
A. 2.
B. 4.
C. 6.
D. 8.
1) phương trình cosx = m có nghiệm khi
2) nghiệm của phương trình \(tan2x-1=0\) là
3) nghiệm của phương trình \(2cos2x=-2\)
Nghiệm của phương trình 2 cos 2 x + 3 sin x − 3 = 0 trong khoảng x ∈ 0 ; π 2
A. x = π/3
B. x = π/4
C. x = π/6
D. x = 5 π/6

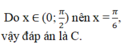
Chú ý: Chúng ta có thể loại ngay phương án D vì 5π/6 ∉ [0; π/2 ] và thay bởi việc giải bài toán như trên, chúng ta có thể sử dụng máy tính để kiểm tra 2 trong số 3 phương án còn lại để xác định đáp án của bài toán.
Đúng 0
Bình luận (0)
Tìm nghiệm x
∈
0
;
π
2
của phương trình sau
4
sin
2
π
-
π
2
-
3
sin
π
2
-
2...
Đọc tiếp
Tìm nghiệm x ∈ 0 ; π 2 của phương trình sau 4 sin 2 π - π 2 - 3 sin π 2 - 2 x = 1 + 2 cos 2 x - π 4
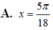
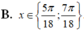
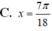
![]()
Tìm các nghiệm
x
∈
0
;
π
2
của phương trình sau
4
sin
2
π
-
x
2
-
3
π
2
-
2
x...
Đọc tiếp
Tìm các nghiệm x ∈ 0 ; π 2 của phương trình sau
4 sin 2 π - x 2 - 3 π 2 - 2 x = 1 + 2 cos 2 x - 3 π 4
A. x = 5 π 8
B. x ∈ 5 π 18 ; 7 π 18
C. x = 7 π 18
D. x ∈ ∅
Ta có:
4 sin 2 π - x 2 - 3 π 2 - 2 x = 1 + 2 cos 2 x - 3 π 4 ⇔ 2 1 - cos 2 π - x - 3 cos 2 x = 1 + 1 + cos 2 x - 3 π 2 ⇔ 2 - 2 cos x - 3 cos 2 x = 2 - sin 2 x ⇔ sin 2 x - 3 cos 2 x = 2 cos x ⇔ 1 2 sin 2 x - 3 2 cos 2 x = cos x ⇔ sin 2 x - π 3 = cos π 3 - x ⇔ x = 5 π 8 + k 2 π 3 x = 5 π 6 + k 2 π
Vì x ∈ 0 ; π 2 nên ta chọn được nghiệm x = 5 π 8
Đáp án A
Đúng 0
Bình luận (0)