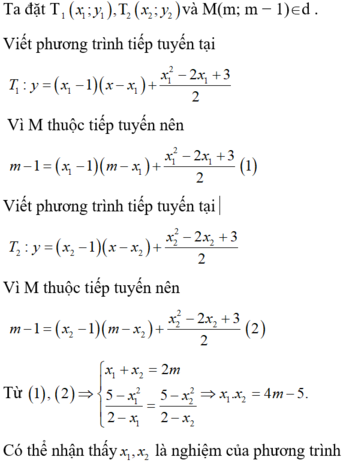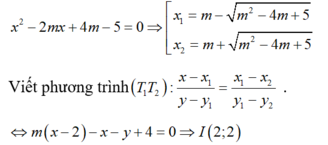Cho Parabol(P): y=-x2 và đường thẳng (d) đi qua điểm I(0;1) và có hệ số góc k. Gọi A và B là các giao điểm của(P) và (d).Gỉa sử A,B lần lượt có hoành độ là x1,x2.Tìm k để trung điểm của đoạn thẳng AB nằm trên trục tung.
Những câu hỏi liên quan
Tìm phương trình đường thẳng (d) đi qua điểm I (0; 1) và cắt parabol (P):
y
x
2
tại hai điểm phân biệt M và N sao cho MN
2
10
A. y 2x + 1; y −2x – 1 B. y 2x + 1; y −2x + 1 C. y 2x + 1; y 2x – 1 D. y −2x + 2; y −2x + 1
Đọc tiếp
Tìm phương trình đường thẳng (d) đi qua điểm I (0; 1) và cắt parabol (P): y = x 2 tại hai điểm phân biệt M và N sao cho MN = 2 10
A. y = 2x + 1; y = −2x – 1
B. y = 2x + 1; y = −2x + 1
C. y = 2x + 1; y = 2x – 1
D. y = −2x + 2; y = −2x + 1
Cho parabol
(
P
)
:
y
x
2
−
2
x
+
3
2
và đường thẳng
d
:
x
−
y
−
1
0
. Qua điểm M tùy ý trên đường thẳng d kẻ 2 tiếp tuyến
M
T
1
,...
Đọc tiếp
Cho parabol ( P ) : y = x 2 − 2 x + 3 2 và đường thẳng d : x − y − 1 = 0 . Qua điểm M tùy ý trên đường thẳng d kẻ 2 tiếp tuyến M T 1 , M T 2 tới (P) (với T 1 , T 2 là các tiếp điểm). Biết đường thẳng T 1 T 2 luôn đi qua điểm I ( a ; b ) cố định. Phát biểu nào sau đây đúng?
A. b ∈ ( − 1 ; 3 ) .
B. a < b .
C. a + 2 b = 5.
D. a . b = 9.
Trong mặt phẳng tọa độ Oxy, cho Parabol(P): y=x2 và đường thẳng (d): y=2(m+1)x-m2-4 (1), (m là tham số)
a) Tìm m để đường thẳng (d) đi qua A(0;-5)
b) Với giá trị nào của m để đường thẳng (d) cắt parabol (P) tại 2 điểm phân biệt có hoành độ x1; x2 thỏa mãn điều kiện: (2x1-1)(x22-2mx2+m2+3)=21
a: Thay x=0 và y=-5 vào (d), ta được:
2(m+1)*0-m^2-4=-5
=>m^2+4=5
=>m=1 hoặc m=-1
b:
PTHĐGĐ là;
x^2-2(m+1)x+m^2+4=0
Δ=(2m+2)^2-4(m^2+4)
=4m^2+8m+4-4m^2-16=8m-12
Để PT có hai nghiệm phân biệt thì 8m-12>0
=>m>3/2
x1+x2=2m+2; x1x2=m^2+4
(2x1-1)(x2^2-2m*x2+m^2+3)=21
=>(2x1-1)[x2^2-x2(2m+2-2)+m^2+4-1]=21
=>(2x1-1)[x2^2+2x2-x2(x1+x2)+x1x2-1]=21
=>(2x1-1)(x2^2+2x2-x1x2-x2^2+x1x2-1]=21
=>(2x1-1)(2x2-1)=21
=>4x1x2-2(x1+x2)+1=21
=>4(m^2+4)-2(2m+2)+1=21
=>4m^2+16-4m-4-20=0
=>4m^2-4m-8=0
=>(m-2)(m+1)=0
=>m=2(nhận) hoặc m=-1(loại)
Đúng 0
Bình luận (0)
cho parabol (P) : y= -x2 -1 và đường thẳng (d) đi qua điểm I (0;-2) và có hệ số góc k
a) tìm k để (d) cắt (P) tại 2 điểm phân biệt
b) gọi A,B là các giao điểm của (d) và (p) và có hoành độ lầ lượt là x1,x2 , tìm k để trung điểm của đoạn thẳng AB nằm trên trục tung
Cho parabol (P): y= -x2 và đường thẳng d đi qua điểm I(0; -1) có hệ số góc k. Viết phương trình đường thẳng (d).
Mục tiêu -500 sp mong giúp đỡ haha
Trong mặt phẳng tọa độ oxy, đường thẳng (d) y=2x-m+3 và Parabol (P) y=x2.
a) Tìm m để đường thẳng (d) đi qua A(1;0)
b) Tìm m để dường thẳng (d) và Parabol (P) cắt nhau tại hai điểm phân biệt có hoành độ lần lượt là x1, x2 thỏa mãn x12 -2x2 +x1.x2 = -12
Lời giải:
a. Để $(d)$ đi qua $A(1;0)$ thì:
$y_A=2x_A-m+3$
$\Leftrightarrow 0=2.1-m+3=5-m$
$\Leftrightarrow m=5$
b.
PT hoành độ giao điểm:
$x^2-(2x-m+3)=0$
$\Leftrightarrow x^2-2x+m-3=0(*)$
Để $(P), (d)$ cắt nhau tại 2 điểm pb thì $(*)$ phải có 2 nghiệm pb $x_1,x_2$
Điều này xảy ra khi:
$\Delta'=1-(m-3)>0\Leftrightarrow 4-m>0\Leftrightarrow m< 4$
Áp dụng định lý Viet: $x_1+x_2=2$ và $x_1x_2=m-3$
Khi đó:
$x_1^2-2x_2+x_1x_2=-12$
$\Leftrightarrow x_1^2-(x_1+x_2)x_2+x_1x_2=-12$
$\Leftrightarrow x_1^2-x_2^2=-12$
$\Leftrightarrow (x_1-x_2)(x_1+x_2)=-12$
$\Leftrightarrow x_1-x_2=-6$
$\Rightarrow x_1=-2; x_2=4$
$m-3=x_1x_2=(-2).4=-8$
$\Leftrightarrow m=-5$ (tm)
Đúng 0
Bình luận (0)
cho đường thẳng (d): y= 2mx+2m-3 và Parabol (P): y=x2
a) Tìm m để đường thẳng (d) đi qua A(1,5)
b) Tìm m để đt (d) tiếp xúc với Parabol (P)
a) (d) đi qua \(A\left(1;5\right)\Rightarrow5=2m+2m-3\Rightarrow4m=8\Rightarrow m=2\)
\(\Rightarrow y=4x+1\)
b) pt hoành độ giao điểm \(x^2-2mx-2m+3=0\)
Để (d) tiếp xúc với (P) thì pt có nghiệm kép \(\Delta=0\)
\(\Delta=\left(2m\right)^2+8m-12=4m^2+8m-12\)
\(\Rightarrow4m^2+8m-12=0\Rightarrow m^2+2m-3=0\Rightarrow\left(m-1\right)\left(m+3\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}m=1\\m=-3\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Cho parabol (P):
y
x
2
và đường thẳng d đi qua điểm A(1;2). Diện tích hình phẳng giới hạn bởi (C) và d có giá trị nhỏ nhất bằng A.
3
4
B.
1
+
2
2
C.
4
3
D.
2
Đọc tiếp
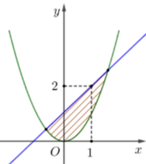
Cho parabol (P): y = x 2 và đường thẳng d đi qua điểm A(1;2). Diện tích hình phẳng giới hạn bởi (C) và d có giá trị nhỏ nhất bằng
A. 3 4
B. 1 + 2 2
C. 4 3
D. 2
Có d qua điểm A(1;2) và có hệ số góc k có phương trình là d; y=k(x-1)+2
Phương trình hoành độ giao điểm: 
Khi đó diện tích hình phẳng
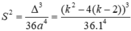
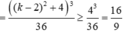
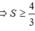
Chọn đáp án C.
*Chú ý diện tích hình phẳng giới hạn bởi parabol
y
=
a
x
2
+
b
x
+
c
và đường thẳng d:y=mx+n có công thức tính nhanh sau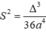 
trong đó Δ là biệt thức của phương trình hoành độ giao điểm:
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, cho đường thẳng (d):\(y=2x-m+1\) (với m là tham số) và parabol (P): .
a) Tìm m để đường thẳng (d) đi qua điểm A (–1; 3).
b) Tìm m để đường thẳng (d) cắt parabol (P) tại hai điểm phân biệt có tọa độ (x1; y1) và (x2; y2) sao cho \(x_1x_2\left(y_1+y_2\right)+6=0\) .
a: Thay x=-1 và y=3 vào (d), ta được:
-2-m+1=3
=>-1-m=3
=>m+1=-3
hay m=-4
Đúng 1
Bình luận (1)
Bài 1: Cho parabol (P) : y = x2 và đường thẳng (d) : y= 3mx + 1 - m2 ( m là tham số)
a) TÌm m để (d) đường thẳng đi qua A( 1; -9)
b) Tìm m để (d) m cắt (P) tại 2 điểm phân biệt có hoành độ x1; x2 thõa mãn x1 + x2 = 2x1x2
Bài 1:
a) Để (d) đi qua A(1;-9) thì
Thay x=1 và y=-9 vào (d), ta được:
\(3m\cdot1+1-m^2=-9\)
\(\Leftrightarrow-m^2+3m+1+9=0\)
\(\Leftrightarrow m^2-3m-10=0\)
\(\Leftrightarrow m^2-5m+2m-10=0\)
\(\Leftrightarrow m\left(m-5\right)+2\left(m-5\right)=0\)
\(\Leftrightarrow\left(m-5\right)\left(m+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m-5=0\\m+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=5\\m=-2\end{matrix}\right.\)
Vậy: Để (d) đi qua A(1;-9) thì \(m\in\left\{5;-2\right\}\)
Đúng 0
Bình luận (0)