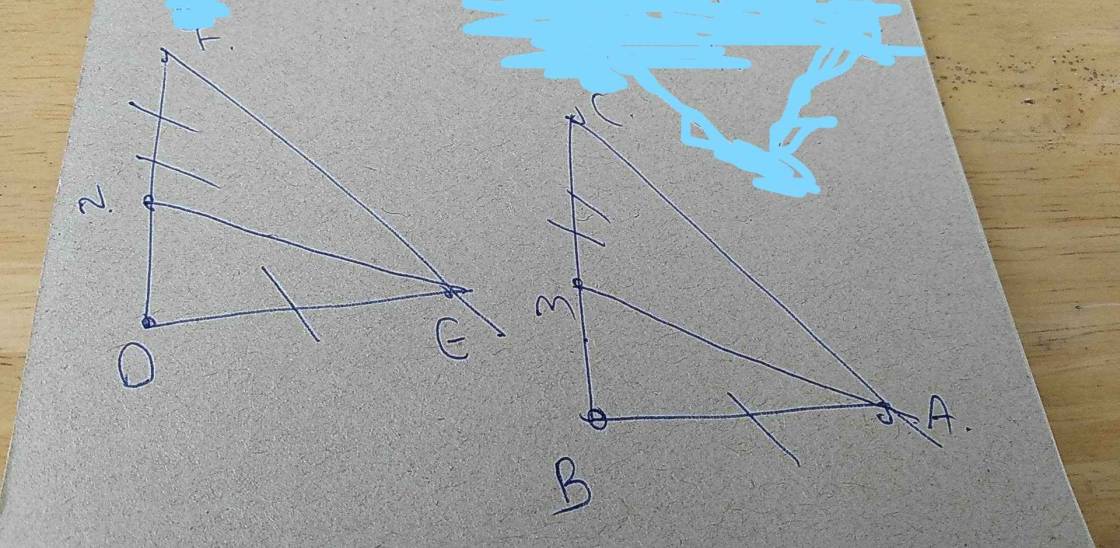
ko cần vẽ hình ạ

Những câu hỏi liên quan
ko cần vẽ hình ạ!
Độ dài đình chéo BD:
\(80:4=20\left(cm\right)\)
Độ dài đường chéo AC:
\(80-20=60\left(cm\right)\)
Diện tích hình thoi:
\(\dfrac{20\times60}{2}=600\left(cm^2\right)\)
Đúng 8
Bình luận (0)
Đường chéo `BD` là: `80xx1:(1+3)=20(cm)`
Đường chéo `AC` là: `80-20=60(cm)`
Diện tích của hình thoi đó là: `20xx60:2=600(cm^2)`
Đúng 7
Bình luận (0)
Độ dài đường chéo BD là:
\(80:\left(1+3\right)\times1=20\left(cm\right)\)
Độ dài đường chéo AC là:
\(80-20=60\left(cm\right)\)
Diện tích hình thoi là:
\(\dfrac{20\times60}{2}=600\left(cm^2\right)\)
Đúng 1
Bình luận (0)
Chỉ cần vẽ hình thôi ạ ko cần giải
\(a,\) Vì AH la đường cao tg ABC cân A nên AH cũng là trung tuyến
Mà H là trung điểm AE nên ABEC là hbh
Mà AE vuông BC tại H nên ABEC là hthoi
\(b,\) Theo tc trung tuyến ứng cạnh huyền thì \(HI=\dfrac{1}{2}AC\)
Vì D,F là trung điểm AH,HC nên DF là đtb
Do đó \(DF=\dfrac{1}{2}AC\)
Vậy \(DF=HI\)
Đúng 2
Bình luận (0)
mik cần gấp ạ, ko cần vẽ hình đâu:
Đọc tiếp
mik cần gấp ạ, ko cần vẽ hình đâu:
giúp em bài 1 với ạ ko cần hình vẽ ,em cần gấp lắm ạ

Bài 1:
a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//BC và \(MN=\dfrac{BC}{2}\)
hay MN//BP và MN=BP
Xét tứ giác BMNP có
MN//BP
MN=BP
Do đó: BMNP là hình bình hành
Đúng 1
Bình luận (0)
mn ơi giúp em bài này với
ko cần hình vẽ cũng dc ạ ( có thì càng tốt mà ko có cũng ko sao ạ)
a: Xét tứ giác BFCE có
D là trung điểm của BC
D là trung điểm của FE
Do dó: BFCE là hình bình hành
b: Xét tứ giác ABFE có
AB//FE
AB=FE
Do đó: ABFE là hình bình hành
mà \(\widehat{FAB}=90^0\)
nên ABFE là hình chữ nhật
Đúng 1
Bình luận (1)
giúp mik vẽ hình với ạ,ko cần giải
 hình ko cần vẽ đâu ạ, em vẽ rồi. Làm giúp em câu 2b thôi
hình ko cần vẽ đâu ạ, em vẽ rồi. Làm giúp em câu 2b thôi
a: \(\widehat{A}=180^0-2\cdot70^0=40^0\)
Đúng 1
Bình luận (0)
các bạn giúp mình giải với ạ, ko cần vẽ hình đâu ạ, mình cảm ơn 
b: Xét ΔMNP vuông tại M có MH là đường cao
nên \(NH\cdot NP=MN^2\left(1\right)\)
Xét ΔMNK vuông tại M có MQ là đường cao
nên \(NQ\cdot NK=MN^2\left(2\right)\)
Từ (1) và (2) suy ra \(NH\cdot NP=NQ\cdot NK\)
Đúng 0
Bình luận (0)
chỉ trả lời phần a bài 4 thôi ạ ko cần vẽ hình
 chi tiết ko cần vẽ hình làm theo chương trinh mới ạ gấp lắm
chi tiết ko cần vẽ hình làm theo chương trinh mới ạ gấp lắm
a: Xét tứ giác AEDF có
\(\widehat{AED}=\widehat{AFD}=\widehat{FAE}=90^0\)
=>AEDF là hình chữ nhật
=>AD cắt EF tại trung điểm của mỗi đường
mà I là trung điểm của EF
nên I là trung điểm của AD
=>A,I,D thẳng hàng
b: Xét ΔBAC có DE//AC
nên \(\dfrac{DE}{AC}=\dfrac{BD}{BC}\)
Xét ΔBAC có DF//AB
nên \(\dfrac{DF}{AB}=\dfrac{CD}{CB}\)
\(\dfrac{DE}{AC}+\dfrac{DF}{AB}=\dfrac{BD}{BC}+\dfrac{CD}{BC}=1\)
=>\(\dfrac{DE}{AB}+\dfrac{DF}{AB}=1\)
=>\(DE+DF=AB\)
=>\(2\cdot\left(DE+DF\right)=2AB\)
=>\(C_{AEDF}=2\cdot AB\) không đổi
Đúng 1
Bình luận (0)