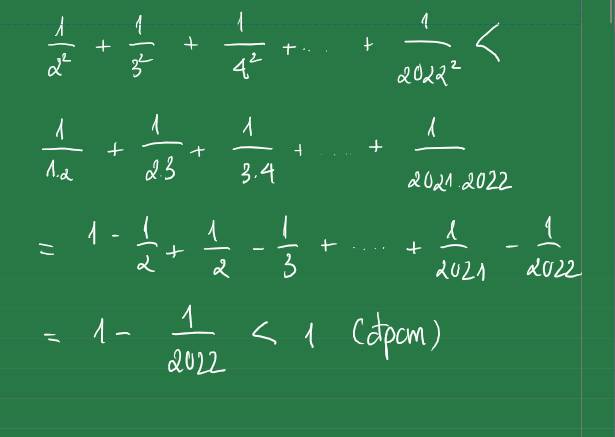Mn giúp em bài này vs ạ

Những câu hỏi liên quan
Giúp mik bài này vs ạ, chỉ cần cậ d thôi ạ( mn giúp em vs em đang cần gấp )
a/ Tam giác AMN cân tại A (gt). \(\Rightarrow\) \(\widehat{AMN}=\widehat{ANM};AM=AN.\)
Xét tam giác AMB và tam giác ANC có:
+ AM = AN (cmt).
+ \(\widehat{AMB}=\widehat{ANC}\left(\widehat{AMN}=\widehat{ANM}\right).\)
+ MB = NC (gt).
\(\Rightarrow\) Tam giác AMB = Tam giác ANC (c - g - c).
\(\Rightarrow\) AB = AC (cặp cạnh tương ứng).
Xét tam giác ABC có: AB = AC (cmt).
\(\Rightarrow\) Tam giác ABC cân tại A.
b/ Tam giác ABC cân tại A (cmt) \(\Rightarrow\) \(\widehat{ABC}=\widehat{ACB}.\)
Mà \(\widehat{ABC}=\widehat{MBH;}\widehat{ACB}=\widehat{NCK}\text{}\) (đối đỉnh).
\(\Rightarrow\) \(\widehat{MBH}=\widehat{NCK}.\)
Xét tam giác MBH và tam giác NCK \(\left(\widehat{BHM}=\widehat{CKN}=90^o\right)\)có:
+ MB = NC (gt).
+ \(\widehat{MBH}=\widehat{NCK}\left(cmt\right).\)
\(\Rightarrow\) Tam giác MBH = Tam giác NCK (cạnh huyền - góc nhọn).
c/ Tam giác MBH = Tam giác NCK (cmt).
\(\Rightarrow\) \(\widehat{BMH}=\widehat{CNK}\) (cặp góc tương ứng).
Xét tam giác OMN có: \(\widehat{NMO}=\widehat{MNO}\) (do \(\widehat{BMH}=\widehat{CNK}\)).
\(\Rightarrow\) Tam giác OMN tại O.
Đúng 0
Bình luận (0)
Mn giúp em bài này vs ạ
Em cảm ơn ạ 🥰




mn giúp em vs ạ. bài này em khó hiểu quá ạ
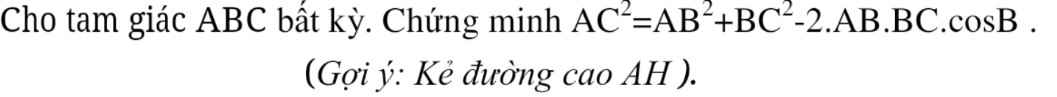
Kẻ AH⊥BC
ta có: \(VP=AB^2+BC^2-2.AB.BC.cosB=AB^2+BC^2-2.AB.BC.\dfrac{BH}{AB}=AB^2+BC^2-2.BH.BC=AB^2-BH^2+BC^2-2.BH.BC+BH^2=AH^2+\left(BC-BH\right)^2=AH^2+CH^2=AC^2=VT\)
Đúng 1
Bình luận (0)
Mn ơi giúp em bài này vs ạ
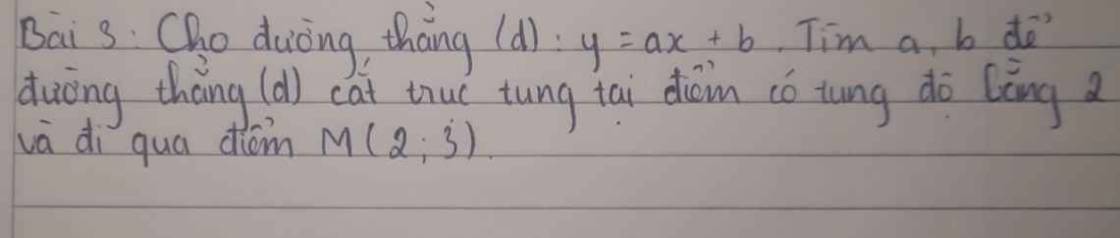
Lời giải:
Vì $(d)$ đi qua điểm $M(2,3)$ nên:
$y_M=ax_M+b\Leftrightarrow 3=2a+b(1)$
Vì $(d)$ cắt trục tung tại điểm có tung độ 2, tức là $(d)$ cắt trục tung tại điểm $(0,2)$
$\Rightarrow 2=a.0+b(2)$
Từ $(1); (2)\Rightarrow b=2; a=\frac{1}{2}$
Đúng 1
Bình luận (0)
Mn làm ơn giúp em bài này vs ạ ! Em đg cần rất gấp ạ ! Em cảm ơn nhiều ạ 
Mn làm ơn giúp em bài này vs ạ ! Em đg cần gấp lắm ạ ! Em cảm ơn 
mn giúp em hai bài này vs ạ em cảm ơn nhìuuu:33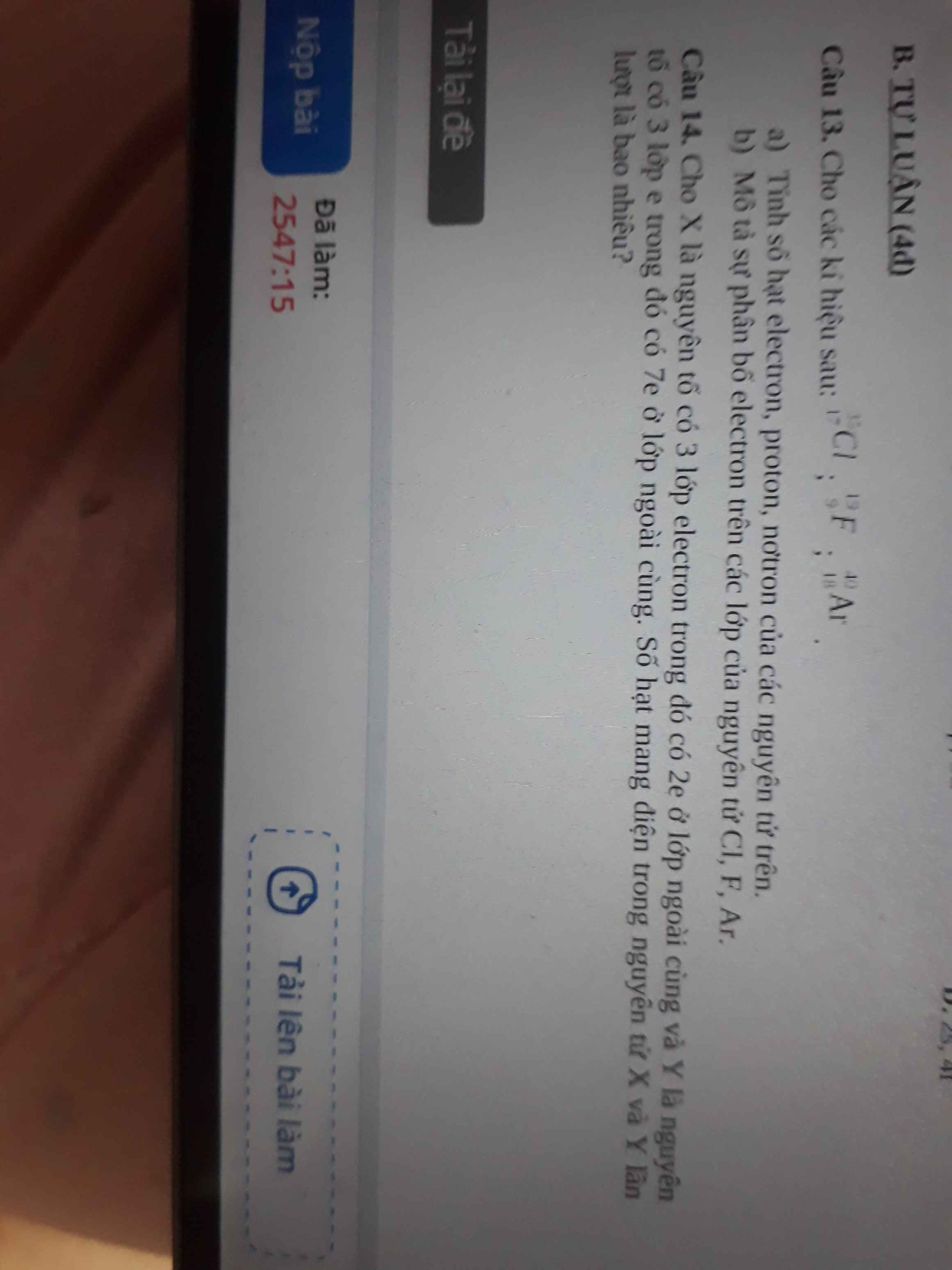
Mn lm ơn giúp em bài này vs ạ ! Em đg cần gấp lắm rồi ạ ! Em cảm ơn 
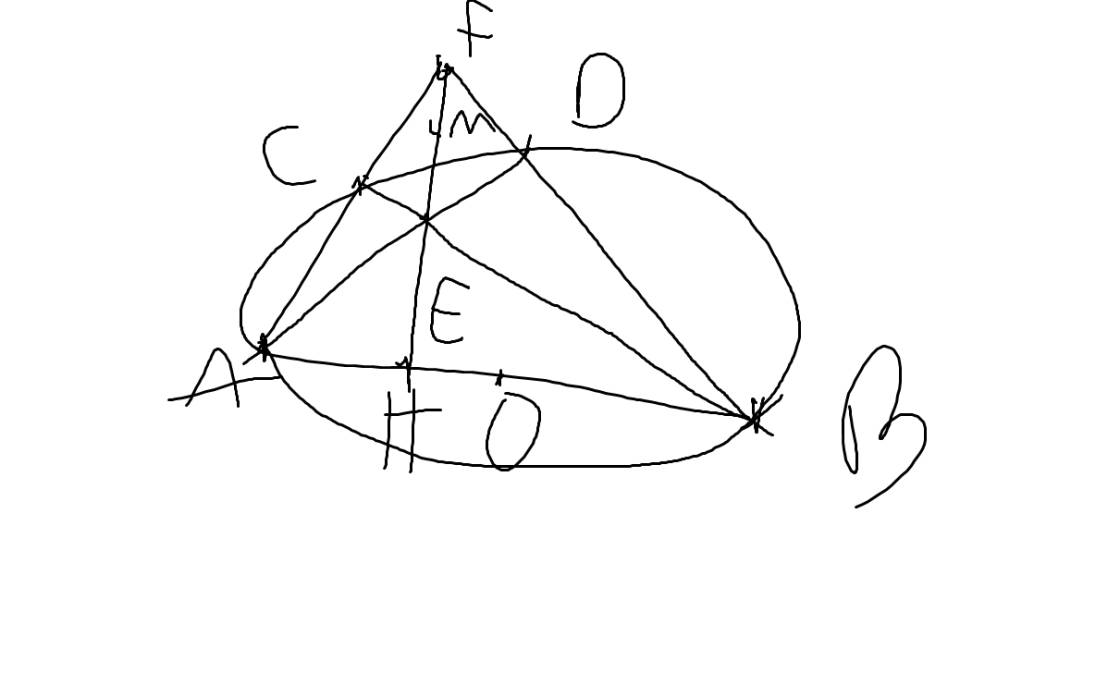
Mn ơi giúp em bài này vs ạ  Vẽ cả hình nx
Vẽ cả hình nx
a: Xét (O) có
ΔABC nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
=>CB\(\perp\)CA tại C
=>CB\(\perp\)AF tại C
Xét tứ giác BHCF có \(\widehat{BHF}=\widehat{BCF}=90^0\)
nên BHCF là tứ giác nội tiếp
=>B,H,C,F cùng thuộc một đường tròn
Đúng 2
Bình luận (0)
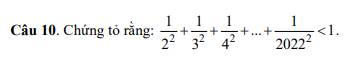
MN GIÚP EM BÀI NÀY VS Ạ
EM CẢM ƠN RẤT NHÌU
(ĐAG CẦN GẤP)