Câu 6: D

Câu 7: D

Câu 8: A

6C
7D
8D

Cho me xin viêm khớp tâm bình cái

đề đâu bạn ơi ?

1, VTCP \(\overrightarrow{AC}=\left(-2;2\right)\); A(4;3)

PTTS : \(\left\{{}\begin{matrix}x=4+2t\\y=3-2t\end{matrix}\right.\)( t là tham số ) 

VTPT ( -2;-2) ; A(4;3) 

PTTQ : \(-2\left(x-4\right)-2\left(y-3\right)=0\Leftrightarrow-2x-2y+14=0\Leftrightarrow x+y-7=0\)

2, AB :  \(VTCP\overrightarrow{AB}=\left(-10;-2\right)\)

Do delta vuông góc với AB nên VTCP AB là VTPT đt delta 

delta \(-10\left(x-2\right)-2\left(y-5\right)=0\Leftrightarrow-10x-2y+30=0\Leftrightarrow5x+y-15=0\)

3, pt đường tròn có dạng  \(\left(x+6\right)^2+\left(y-1\right)^2=R^2\)

do pt (C1) thuộc A nên \(\left(4+6\right)^2+\left(3-1\right)^2=R^2\Leftrightarrow104=R^2\)

=> \(\left(C1\right):\left(x+6\right)^2+\left(y-1\right)^2=104\)

4, tâm \(I\left(3;4\right)\)

\(R=\dfrac{AC}{2}=\dfrac{\sqrt{4+4}}{2}=\dfrac{\sqrt{8}}{2}\Rightarrow R^2=2\)

\(\left(C2\right):\left(x-3\right)^2+\left(y-4\right)^2=2\)

1: vecto AC=(-2;2)

=>VTCP là (-2;2); vtpt là (2;2)

2: vecto AB=(-10;-2)=(5;1)

=>VTPT của Δ là (5;1)

vtcp của Δ là (-1;5)

\(\overrightarrow{AC}=\left(-2;2\right)=2\left(-1;1\right)\) nên đường thẳng AC nhận \(\left(-1;1\right)\) là 1 vtcp và \(\left(1;1\right)\) là 1 vtpt

b.

\(\overrightarrow{BA}=\left(10;2\right)=2\left(5;1\right)\) ; mà \(\Delta\perp AB\) nên \(\Delta\) nhận (5;1) là 1 vtpt và \(\left(1;-5\right)\) là 1 vtcp

a: Xét ΔAEB vuông tại E và ΔAFC vuông tại F có

\(\hat{EAB}\) chung

Do đó: ΔAEB~ΔAFC

=>\(\frac{AE}{AF}=\frac{AB}{AC}\)

=>\(\frac{AE}{AB}=\frac{AF}{AC}\)

=>\(AE\cdot AC=AF\cdot AB\)

b: Xét ΔAEF và ΔABC có

\(\frac{AE}{AB}=\frac{AF}{AC}\)

góc EAF chung

Do đó: ΔAEF~ΔABC

=>\(\hat{AEF}=\hat{ABC}\)

c: Ta có: ΔBEM vuông tại E

mà EI là đường trung tuyến

nên IE=IB

=>ΔIBE cân tại I

=>\(\hat{IEB}=\hat{IBE}\)

mà \(\hat{FEB}=\hat{IBE}\) (hai góc so le trong, FE//BM)

nên \(\hat{FEB}=\hat{IEB}\)

=>EB là phân giác của góc FED

Gọi K là giao điểm của AH và BC

Xét ΔABC có

BE,CF là các đường cao

BE cắt CF tại H

Do đó: H là trực tâm của ΔABC

=>AH⊥BC tại K

Xét ΔHFB vuông tại F và ΔHEC vuông tại E có

\(\hat{FHB}=\hat{EHC}\) (hai góc đối đỉnh)

Do đó: ΔHFB~ΔHEC

=>\(\frac{HF}{HE}=\frac{HB}{HC}\)

=>\(\frac{HF}{HB}=\frac{HE}{HC}\)

Xét ΔHFE và ΔHBC có

\(\frac{HF}{HB}=\frac{HE}{HC}\)

góc FHE=góc BHC

Do đó: ΔHFE~ΔHBC

=>\(\hat{HEF}=\hat{HCB}\)

mà \(\hat{HCB}=\hat{BAK}\left(=90^0-\hat{ABC}\right)\)

nên \(\hat{HEF}=\hat{BAK}\) (1)

Xét ΔHEA vuông tại E và ΔHKB vuông tại K có

\(\hat{EHA}=\hat{KHB}\) (hai góc đối đỉnh)

Do đó: ΔHEA~ΔHKB

=>\(\frac{HE}{HK}=\frac{HA}{HB}\)

=>\(\frac{HE}{HA}=\frac{HK}{HB}\)

Xét ΔHEK và ΔHAB có

\(\frac{HE}{HA}=\frac{HK}{HB}\)

góc EHK=góc AHB

Do đó: ΔHEK~ΔHAB

=>\(\hat{HEK}=\hat{HAB}=\hat{BAK}\left(2\right)\)

TỪ (1),(2) suy ra \(\hat{HEK}=\hat{HEF}\)

=>EB là phân giác của góc FEK

mà EB là phân giác của góc FED

và EK và ED có điểm chung là E; D và K đều nằm trên cạnh BC

nên K trùng với D

=>A,H,D thẳng hàng

8:

a: Xét tứ giác ADCF có

E là trungd diểm chung của AC và DF

=>ADCF là hbh

=>AD//CF và AD=CF

=>CF=DB

b: Xét ΔBDC và ΔFCD có

BD=CF

DC chung

BC=DF

=>ΔBDC=ΔFCD

c: Xét ΔABC có AD/AB=AE/AC=1/2

nên DE//BC và DE=1/2BC

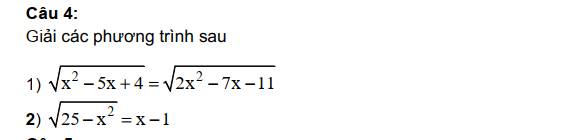
1: =>2x^2-7x-11=x^2-5x+4

=>x^2-2x-15=0

=>(x-5)(x+3)=0

=>x=5 hoặc x=-3

2: =>x>=1 và 25-x^2=x^2-2x+1

=>x^2-2x+1-25+x^2=0 và x>=1

=>2x^2-2x-24=0 và x>=1

=>x=4

1.

Bình phương hai vế pt đã cho ta được:

\(x^2-5x+4=2x^2-7x-11\)

\(\Rightarrow x^2-2x-15=0\)

\(\Rightarrow x=5\) hoặc \(x=-3\)

Thay lần lượt hai giá trị trên vào pt đã cho ta thấy đều thỏa mãn

Vậy nghiệm của pt là \(S=\left\{-3;5\right\}\)

2.

Bình phương 2 vế pt đã cho:

\(25-x^2=\left(x-1\right)^2\)

\(\Rightarrow25-x^2=x^2-2x-1\)

\(\Rightarrow2x^2-2x-24=0\)

\(\Rightarrow x=4\) hoặc \(x=-3\)

Lần lượt thay các giá trị trên vào pt đã cho ta thấy chỉ có \(x=4\) thỏa mãn

Vậy nghiệm của pt đã cho là \(S=\left\{4\right\}\)