Cho hình thang vuông ABCD vuông tại A và B, có AB=2a, BC=a, AD=3a, kẻ AH vuông góc với CD. Tính AH

Những câu hỏi liên quan
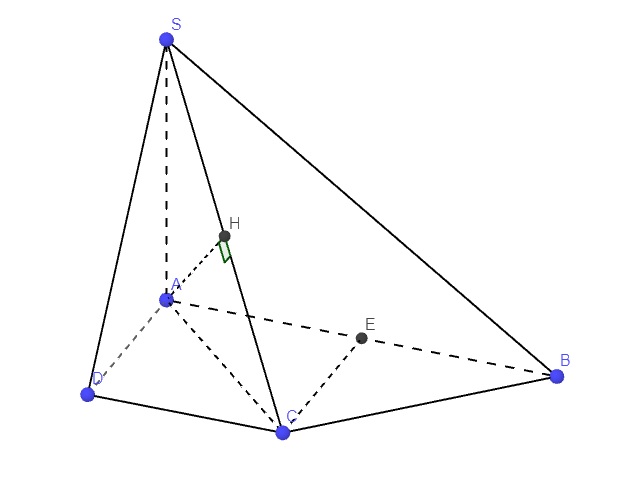
Cho hình chóp sabcd có abcd là hình thang vuông tại a,d. Ab=2a, ad=cd=a. Sa=a√2, sa vuông góc abcd a, (sb,(abcd))=? (Sc,(abcd)=? b, kẻ ah vuông góc sc tại h. Ak vuông góc sd tại k (Ah,(sad))=? (Sb,(sac)=?
a.
\(SA\perp\left(ABCD\right)\Rightarrow AB\) là hình chiếu vuông góc của SB lên (ABCD)
\(\Rightarrow\widehat{SBA}=\left(SB;\left(ABCD\right)\right)\)
\(tan\widehat{SBA}=\dfrac{SA}{AB}=\dfrac{\sqrt{2}}{2}\Rightarrow\widehat{SBA}\approx35^016'\)
Tương tự \(SA\perp\left(ABCD\right)\Rightarrow\widehat{SCA}=\left(SC;\left(ABCD\right)\right)\)
\(AC=\sqrt{AD^2+DC^2}=a\sqrt{2}\)
\(\Rightarrow tan\widehat{SCA}=\dfrac{SA}{AC}=1\Rightarrow\widehat{SCA}=45^0\)
b.
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp AB\\AB\perp AD\end{matrix}\right.\) \(\Rightarrow AB\perp\left(SAD\right)\)
\(\Rightarrow\left(AH;\left(SAD\right)\right)=90^0-\left(AH;AB\right)=90^0-\widehat{HAB}\)
Gọi E là trung điểm AB \(\Rightarrow ADCE\) là hình vuông \(\Rightarrow\widehat{ACE}=45^0\)
Tam giác BCE vuông cân tại E (do \(EB=EC=a\)) nên \(\widehat{ECB}=45^0\)
\(\Rightarrow\widehat{ACB}=90^0\) hay \(BC\perp AC\Rightarrow BC\perp\left(SAC\right)\) (do \(SA\perp BC\))
\(\Rightarrow BC\perp AH\Rightarrow AH\perp\left(SBC\right)\Rightarrow AH\perp BH\)
Hay tam giác ABH vuông tại H
\(AH=\dfrac{SA.AC}{\sqrt{SA^2+AC^2}}=a\)
\(\Rightarrow cos\widehat{HAB}=\dfrac{AH}{AB}=\dfrac{1}{2}\Rightarrow\widehat{HAB}=60^0\)
\(\Rightarrow\widehat{HAB}=60^0\Rightarrow\left(AH;\left(SAD\right)\right)=30^0\)
Theo cmt \(BC\perp\left(SAC\right)\Rightarrow\left(SB;\left(SAC\right)\right)=\widehat{BSC}\)
\(SC=\sqrt{SA^2+AC^2}=2a\) ; \(SB=\sqrt{SA^2+AB^2}=a\sqrt{6}\)
\(\Rightarrow cos\widehat{BSC}=\dfrac{SC}{SB}=\dfrac{\sqrt{6}}{3}\Rightarrow\widehat{BSC}\approx35^016'\)
Đúng 0
Bình luận (0)
Cho hình vuông ABCD vuông tại A có AB//CD và AB<CD. Kẻ AH vuông góc với BD tại H. Tính BH và diện tích hình thang ABCD nếu biết BC=13cm, CD=14cm và DB=15cm
Cho hình chóp SABCD có đáy là hình thang vuông tại A và D. AB=2a, AD=DC=a. Kẻ AH vuông góc với SC (H thuộc SC). E là trung điểm của AB. Sa vuông góc với (ABCD) và SA=a căn 3. Tính góc giữa a)(SBC) và (ABCD) b)(SAD) và (SAC) c)(SBC) và (SCD)
Cho hình thang vuông ABCD có góc A góc D 900 , AB CD. Kẻ AH vuông góc với BD tại H, AH cắt DC tại điểm E. a) Chứng minh AHD đồng dạng với BAD. b) Chứng minh hệ thức 2 AD AB.DE c) Biết AD 3cm, AB 4cm, tính độ dài đoạn DE và diện tích tứ giác ABED. d) Gọi N là hình chiếu của B lên đường thẳng CD, trên tia đối của tia EA lấy điểm M sao cho AE.EN DE.EM. Chứng minh BE vuông góc với MD. giúp mình câu a b c với
Đọc tiếp
Cho hình thang vuông ABCD có góc A= góc D= 900 , AB > CD. Kẻ AH vuông góc với BD tại H, AH cắt DC tại điểm E. a) Chứng minh AHD đồng dạng với BAD. b) Chứng minh hệ thức 2 AD AB.DE c) Biết AD = 3cm, AB = 4cm, tính độ dài đoạn DE và diện tích tứ giác ABED. d) Gọi N là hình chiếu của B lên đường thẳng CD, trên tia đối của tia EA lấy điểm M sao cho AE.EN = DE.EM. Chứng minh BE vuông góc với MD.
giúp mình câu a b c với
a: Xét ΔAHD vuông tại H và ΔBAD vuông tại A có
góc D chung
=>ΔAHD đồng dạng với ΔBAD
b; Xét ΔDEA vuông tại D và ΔADB vuông tại A có
góc DEA=góc ADB
=>ΔDEA đồng dạng với ΔADB
=>DE/AD=AD/AB
=>AD^2=DE*AB
c: AD^2=DE*AB
=>DE=3^2/4=2,25cm
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có SA vuông góc với mp đáy (ABCD) và ABCD là hình thang vuông tại A, đáy lớn AB, AB=2a, AD=CD=a. Gọi H là hình chiếu vuông góc của A lên SC và E là trung điểm của AB
a, CMR: (SCD) \(\perp\)(SAD) và AH \(\perp\)(SBC)
b, Biết góc giữa 2 mp (SCD) và (ABCD) bằng 300. Tính góc giữa 2 mp (SAD) và (SCE)?
Cho hình chóp S.ABCD có SA vuông góc với mp đáy (ABCD) và ABCD là hình thang vuông tại A, đáy lớn AB, AB=2a, AD=CD=a. Gọi H là hình chiếu vuông góc của A lên SC và E là trung điểm của AB
a, CMR: (SCD) ⊥(SAD) và AH ⊥(SBC)
b, Biết góc giữa 2 mp (SCD) và (ABCD) bằng 300. Tính góc giữa 2 mp (SAD) và (SCE)?
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\\CD\perp AD\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAD\right)\Rightarrow\left(SCD\right)\perp\left(SAD\right)\)
\(AC=\sqrt{AD^2+CD^2}=a\sqrt{2}\)
\(BC=\sqrt{BE^2+CE^2}=a\sqrt{2}\)
\(\Rightarrow AC^2+BC^2=AB^2\Rightarrow AC\perp BC\)
\(\Rightarrow BC\perp\left(SAC\right)\Rightarrow BC\perp AH\Rightarrow AH\perp\left(SBC\right)\)
b.
\(CD\perp\left(SAD\right)\Rightarrow\widehat{SDA}\) là góc giữa (SCD) và (ABCD)
\(\Rightarrow\widehat{SDA}=30^0\Rightarrow SA=AD.tan30^0=\dfrac{a\sqrt{3}}{3}\)
Ta có: \(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp AD\\AD\perp AB\end{matrix}\right.\) \(\Rightarrow AD\perp\left(SAB\right)\)
Qua S kẻ đường thẳng d song song AD
Do \(AD||CE\) \(\Rightarrow\) d là giao tuyến (SAD) và (SCE)
Mà \(d\perp\left(SAB\right)\Rightarrow\widehat{ASE}\) là góc giữa (SAD) và (SCE)
\(AE=\dfrac{AB}{2}=a\)
\(tan\widehat{ASE}=\dfrac{AE}{SA}=\sqrt{3}\Rightarrow\widehat{ASE}=60^0\)
Đúng 2
Bình luận (2)
cho hình thang ABCD có AB//CD và AB<CD. Kẻ AH vuông góc với CD tại H
Chứng minh: Tứ giác ABCH là hình thang vuông
AB//CD
AH\(\perp\)DC
Do đó: AH\(\perp\)AB
Xét tứ giác ABCH có AB//CH
nên ABCH là hình thang
Hình thang ABCH có AB\(\perp\)AH
nên ABCH là hình thang vuông
Đúng 0
Bình luận (0)
Cho hình thang cân ABCD có AB song song với CD , cạnh AD vuông góc với đường chéo AC. Kẻ đường cao AH, BK . Biết AH = 12cm; DH =9cm.
a) Tính AD; AC; HC; số đo của góc DAB
b) Tính AB; diện tích ABCH; chu vi ABCD
c) Từ K kẻ KM vuông góc AD; KN vuông góc AC. AMKN là hình gì? Tính MN
1. Cho tam giác ABC có góc A 90 độ , góc C 30 độ. Từ trung điểm E của cạnh AB vẽ đường thẳng vuông góc với AB cắt BC ở F.a) Tứ giác AEFC là hình gì? Vì sao?b) Tính độ đà các cạnh của tứ giác AEFC, biết AB 3cm.2. Cho hình thang ABCD có góc A góc B 90 độ ; ABBC1/2AD3cm.a) Tính các góc của hình thang .b) Chứng minh AC vuông góc với CDc) Tính chu vi hình tahng.3. Chứng minh rằng tứ giác ABCD là hình thang (AD//BC) khi và chỉ khi phân giác của góc Avaf góc B vuông góc với nhau.4. Cho hình thang câ...
Đọc tiếp
1. Cho tam giác ABC có góc A = 90 độ , góc C = 30 độ. Từ trung điểm E của cạnh AB vẽ đường thẳng vuông góc với AB cắt BC ở F.
a) Tứ giác AEFC là hình gì? Vì sao?
b) Tính độ đà các cạnh của tứ giác AEFC, biết AB= 3cm.
2. Cho hình thang ABCD có góc A= góc B = 90 độ ; AB=BC=1/2AD=3cm.
a) Tính các góc của hình thang .
b) Chứng minh AC vuông góc với CD
c) Tính chu vi hình tahng.
3. Chứng minh rằng tứ giác ABCD là hình thang (AD//BC) khi và chỉ khi phân giác của góc Avaf góc B vuông góc với nhau.
4. Cho hình thang cân ABCD có AD//BC, AB = 3cm, CD= 6cm, AD= 2.5cm. Vẽ 2 đường cao AH, BK. Tính DH,DK,AH
Cho hình thang cân ABCD (AB // CD, AB < CD), biết AC vuông góc với BD . Gọi M, N lần lượt là trung điểm của AD và BC. Kẻ AH vuông góc với CD (H thuộc CD) biết AH=10cm . Khi đó, độ dài MN là
A.9cm B.10cm C.6cm D.8cm