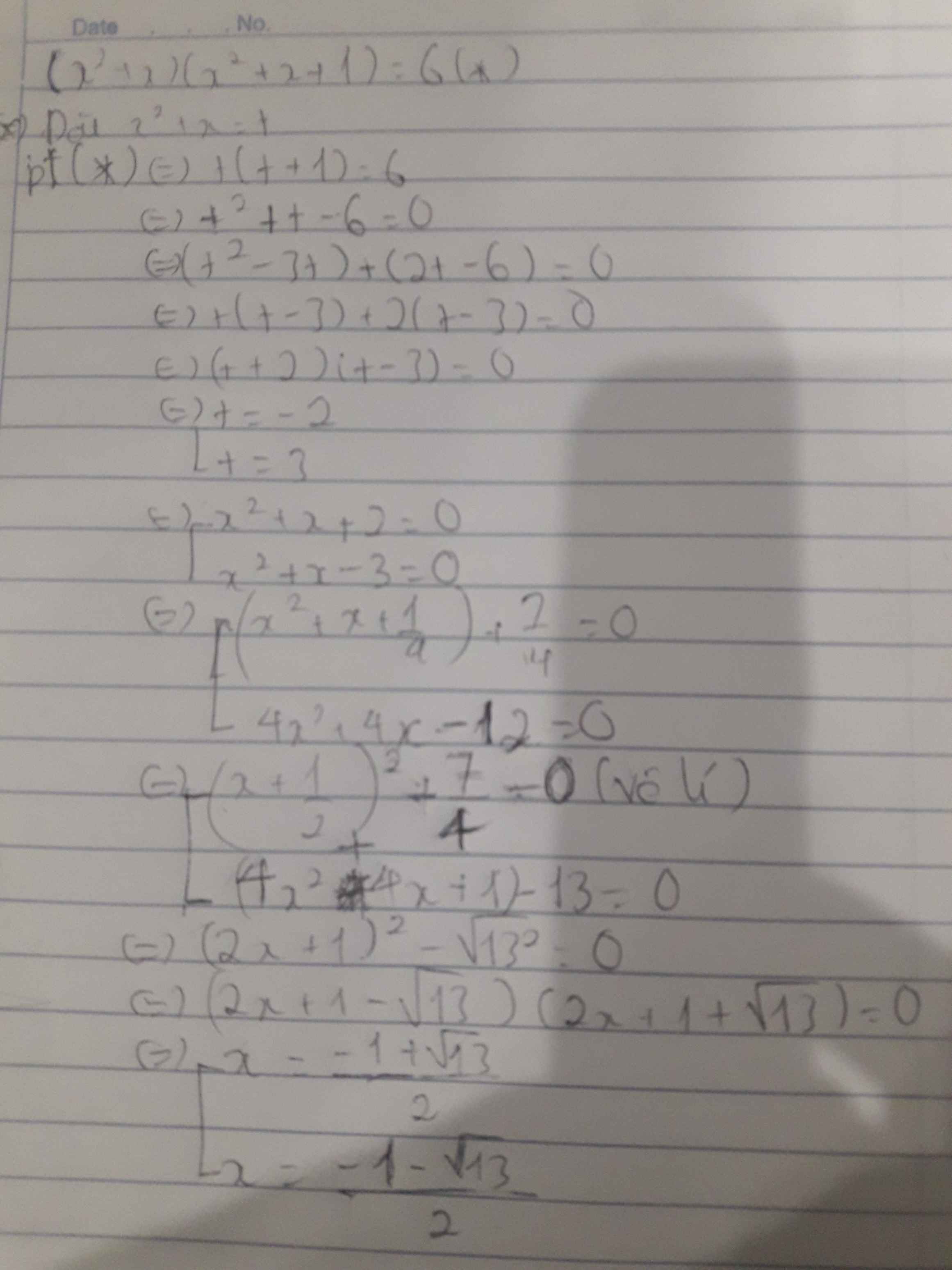1C

2A

1C        2A

bài 1 : a,ta có 3/x-1 =4/y-2=5/z-3 =>  x-1/3=y-2/4=z-3/5 

áp dụng .... => x-1+y-2+z-3 / 3+4+5 = x+y+z-1-2-3/3+4+5 = 12/12=1

do x-1/3 = 1 => x-1 = 3 => x= 4 ( tìm y,z tương tự

Bài 1: 

a) Ta có: 3/x - 1 = 4/y - 2 = 5/z - 3 => x - 1/3 = y - 2/4 = z - 3/5 áp dụng ... =>x - 1 + y - 2 + z - 3/3 + 4 + 5 = x + y + z - 1 - 2 - 3/3 + 4 + 5 = 12/12 = 1 do x - 1/3 = 1 => x - 1 = 3 => x = 4 ( tìm y, z tương tự )

cũng dễ thôi

1 

\(\left(x-2\right):2.3=6\)

\(\Leftrightarrow\left(x-2\right):2=2\)

\(\Leftrightarrow\left(x-2\right)=4\)

\(\Leftrightarrow x=4+2=6\)

c) ta có

\(\left[\left(2x+1\right)+1\right]m:2=625\)

\(\Leftrightarrow\left[\left(2x+1\right)+1\right]\left\{\left[\left(2x+1\right)-1\right]:2+1\right\}=1250\)

\(\Leftrightarrow\left(2x+1\right)^2+1-1:2+1=1250\)

\(\Leftrightarrow\left(2x+1\right)^2+1-2+1=1250\)

\(\Leftrightarrow\left(2x+1\right)^2+1-2=1249\)

\(\Leftrightarrow\left(2x+1\right)^2+1=1251\)

\(\Leftrightarrow\left(2x+1\right)^2=1250\)

...

2

\(\left(x-\frac{1}{2}\right).\frac{5}{3}=\frac{7}{4}-\frac{1}{2}\)

\(\Leftrightarrow\left(x-\frac{1}{2}\right).\frac{5}{3}=\frac{5}{4}\)

\(\Leftrightarrow\left(x-\frac{1}{2}\right)=\frac{5}{4}:\frac{5}{3}\)

\(\Leftrightarrow\left(x-\frac{1}{2}\right)=\frac{5}{4}.\frac{3}{5}\)

\(\Leftrightarrow x-\frac{1}{2}=\frac{3}{4}\)

\(\Leftrightarrow x=\frac{3}{4}+\frac{1}{2}=\frac{5}{4}\)

Ta có

( 3 x   –   1 ) 2   +   2 ( x   +   3 ) 2   +   11 ( 1   +   x ) ( 1   –   x )   =   6     ⇔   ( 3 x ) 2   –   2 . 3 x . 1   +   1 2   +   2 ( x 2   +   6 x   +   9 )   +   11 ( 1   –   x 2 )   =   6     ⇔   9 x 2   –   6 x   +   1   +   2 x 2   +   12 x   +   18   +   11   –   11 x 2   =   6     ⇔   ( 9 x 2   +   2 x 2   –   11 x 2 )   +   ( - 6 x   +   12 x )   =   6   –   1   –   11   –   18

ó 6x = -24 ó x = -4

Vậy x = -4

Đáp án cần chọn là: A

d. (x - 3)(x² + 3x + 9) + x(x + 2)(2 - x) = 1

<=> x³ - 9 + (x² + 2x)(2 - x) = 1

<=> x³ - 9 + 2x² - x³ + 4x - 2x² = 1

<=> 4x = 10

<=> x = \(\dfrac{10}{4}=\dfrac{5}{2}\)

d)(x - 3)(x^2 + 3x + 9) + x(x + 2)(2 - x) = 1

\(<=> x^3-27-x(x^2-4)=1\)

\(<=> x^3-27-x^3-4x=1<=>-4x=28<=> x=-7\)

=> ptrình có tập nghiệm S={-7}

e) (x + 1)^3 - (x - 1)^3 - 6(x - 1)^2 = -19

\(<=> x^3+3x^2+3x+1-(x^3-3x^2+3x-1)-6(x^2-2x+1)+19=0\)

\(<=>x^3+3x^2+3x+1-x^3+3x^2-3x+1-6x^2+12x-6+19=0\)

\(<=>12x=15<=>x=12/15 \)

=> ptrình có tập nghiệm S={12/15}

Hình như sai đề

\(\Leftrightarrow\left(x^2+x\right)^2+\left(x^2+x\right)-6=0\)

\(\Leftrightarrow\left(x^2+x+3\right)\left(x^2+x-2\right)=0\)

=>(x+2)(x-1)=0

=>x=-2 hoặc x=1

\(\Leftrightarrow x^4+x^3+x^2+x^3+x^2+x=0\)

\(\Leftrightarrow x^4+2x^3+2x^2+x=0\)

\(\Leftrightarrow x^3\left(x+2\right)+x\left(2+x\right)=0\)

\(\Leftrightarrow\left(x+2\right)\left(x^3+x\right)=0\)

\(\Leftrightarrow x\left(x+2\right)\left(x^2+1\right)=0\)

\(\Leftrightarrow x\left(x+2\right)\left(x+1\right)\left(x+1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-2\\x=-1\end{matrix}\right.\)

\(\left(x^2+x\right)\left(x^2+x+1\right)=0\)

\(x\left(x+1\right)\left(x^2+x+1\right)=0\)

=> x=0 hoặc x+1=0   (do \(x^2+x+1\ne0\))

                      x=-1

Vậy...