1 1/2 x 37 +3/2 x 62 + 3/2

Những câu hỏi liên quan
a/ 27 + x =62 x b/ 17 - 2 x =9 x c/ 3(x – 5) -11 = 37
Tìm số tự nhiên x lớn nhất, biết:
37, 62, 7 : x được các số dư lần lượt là 1, 2, 3.
37 : x dư 1 => 36 \(⋮\)x
62 : x dư 2 => 60 \(⋮\)x
7 : x dư 3 => 4 \(⋮\)x
Để x lớn nhất => x = ƯCLN(36;60;4) = 4
a) Tim x biet:
1/3 + 1/12 + 1/30 +...+ 2/x(x + 1) (x + 2)
b) Tinh:
(1 + 37) . (1 + 37/2) . (1 + 37/3)...(1 + 37/39)
(1 + 39) . (1 + 39/2) . (1 + 39/3)...(1 + 39/37)
Vo câu lần trước của cậu xem câu của tớ có đúng ko
Đúng 0
Bình luận (0)
tính nhanh nếu có thể
d) 37 . 62 + 38 . 37 - 170
e) 32 + 2 . (18 - 3 x 5)
f) 32 [(52 - 3) : 11] 24
Bạn gọi là tính nhanh nhé :
d ) 37.62 + 38.37 - 170
= 37.(62 + 38 ) - 170
= 37.100 - 170
= 3700 - 170
= 3530
e ) 32 + 2.( 18 - 3.5 )
= 32 + 2.( 18 - 15 )
= 32 + 2.3
= 9 + 2.3
= 9 + 6
= 15
f ) 32[( 52 - 3 ) : 11 ]24
= 32[( 25 - 3 ) : 11 ]24
= 32[ 22 : 11 ]24
= 32.2.24
= 9.2.24
= 18.24
= 432
Câu f chỗ 18.24 cậu có thể bấm máy tính nhé !
Chúc bạn học tốt ! ![]()
Đúng 0
Bình luận (2)
Giải các phương trình:
a
)
(
x
+
3
)
(
x
−
3
)
3
+
2
x
(
1...
Đọc tiếp
Giải các phương trình:
a ) ( x + 3 ) ( x − 3 ) 3 + 2 = x ( 1 − x ) b ) x + 2 x − 5 + 3 = 6 2 − x c ) 4 x + 1 = − x 2 − x + 2 ( x + 1 ) ( x + 2 )
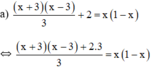
⇔ (x + 3)(x – 3) + 2.3 = 3x(1 – x)
⇔ x 2 − 9 + 6 = 3 x − 3 x 2 ⇔ x 2 − 9 + 6 − 3 x + 3 x 2 = 0 ⇔ 4 x 2 − 3 x − 3 = 0
Có a = 4; b = -3; c = -3 ⇒ Δ = ( - 3 ) 2 – 4 . 4 . ( - 3 ) = 57 > 0
Phương trình có hai nghiệm
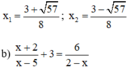
Điều kiện xác định: x ≠ 5; x ≠ 2.
Quy đồng và khử mẫu ta được :
(x + 2)(2 – x) + 3(2 – x)(x – 5) = 6(x – 5)
⇔ 4 − x 2 + 6 x − 3 x 2 − 30 + 15 x = 6 x − 30 ⇔ 4 − x 2 + 6 x − 3 x 2 − 30 + 15 x − 6 x + 30 = 0 ⇔ − 4 x 2 + 15 x + 4 = 0
Có a = -4; b = 15; c = 4 ⇒ Δ = 15 2 – 4 . ( - 4 ) . 4 = 289 > 0
Phương trình có hai nghiệm phân biệt:
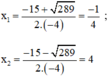
Cả hai giá trị đều thỏa mãn điều kiện.
Vậy phương trình có tập nghiệm 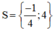
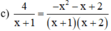
Điều kiện xác định: x ≠ -1; x ≠ -2.
Quy đồng và khử mẫu ta được:
4 ⋅ ( x + 2 ) = − x 2 − x + 2 ⇔ 4 x + 8 = − x 2 − x + 2 ⇔ 4 x + 8 + x 2 + x − 2 = 0 ⇔ x 2 + 5 x + 6 = 0
Có a = 1; b = 5; c = 6 ⇒ Δ = 5 2 – 4 . 1 . 6 = 1 > 0
⇒ Phương trình có hai nghiệm phân biệt:
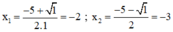
Chỉ có nghiệm x 2 = - 3 thỏa mãn điều kiện xác định.
Vậy phương trình có nghiệm x = -3.
Đúng 0
Bình luận (0)
Rút gọn
A=x(5x-3)-x^2(x-1)+x(x^2-62)-10+3x B=x(x^2+x+1)-x^2(x+1)-x+5
C=-3xy(-x+5y)+5y^2(3x-2y)+2(5y^2-3/2x^2y-2)
D=(3-x-6y)(x^2+2xy+4y^2)-3(x^3-8y^3+10)
\(A=5x^2-3x-x^3+x^2+x^3-62x-10+3x\\ A=6x^2-62x-10\\ B=x^3+x^2+x-x^3-x^2-x+5=5\\ C=3x^2y-15xy^2+15xy^2-10y^3+10y^2-3x^2y-4=-4\)
Đúng 2
Bình luận (0)
b: Ta có: \(B=x\left(x^2+x+1\right)-x^2\left(x+1\right)-x+5\)
\(=x^3+x^2+x-x^3-x^2-x+5\)
=5
Đúng 1
Bình luận (0)
1/3 x + 1/2 = -4/3
-2/3 - 4/3 x = -1/2
5/2 - 2 (x-1) = -2/3
7/-2 x - 1/3 = -1/2
8/5 - 1/2 : x = 8/3
-5/4 x - 1/2 x = -7/3
ét ô ét
+) \(\dfrac{1}{3}x=-\dfrac{4}{3}-\dfrac{1}{2}=-\dfrac{11}{6}\)
\(x=-\dfrac{11}{6}:\dfrac{1}{3}=-\dfrac{11}{2}\)
+) \(\dfrac{4}{3}x=-\dfrac{2}{3}+\dfrac{1}{2}=-\dfrac{1}{6}\)
\(x=-\dfrac{1}{6}:\dfrac{4}{3}=-\dfrac{1}{8}\)
+) \(2\left(x-1\right)=\dfrac{5}{2}+\dfrac{2}{3}=\dfrac{19}{6}\)
\(x-1=\dfrac{19}{12}\)
\(x=\dfrac{31}{12}\)
Đúng 2
Bình luận (0)
\(\dfrac{1}{3}x+\dfrac{1}{2}=-\dfrac{4}{3}\)
\(\dfrac{1}{3}x=\left(-\dfrac{4}{3}\right)-\dfrac{1}{2}\)
\(\dfrac{1}{3}x=-\dfrac{11}{6}\)
\(x=\left(-\dfrac{11}{6}\right):\dfrac{1}{3}\)
\(x=-\dfrac{11}{2}\)
\(-\dfrac{2}{3}-\dfrac{4}{3}x=-\dfrac{1}{2}\)
\(\dfrac{4}{3}x=\left(-\dfrac{2}{3}\right)-\dfrac{-1}{2}\)
\(\dfrac{4}{3}x=-\dfrac{1}{6}\)
\(x=\left(-\dfrac{1}{6}\right):\dfrac{4}{3}\)
\(x=-\dfrac{1}{8}\)
\(\dfrac{5}{2}-2\left(x-1\right)=-\dfrac{2}{3}\)
\(2\left(x-1\right)=\dfrac{5}{2}-\left(-\dfrac{2}{3}\right)\)
\(2\left(x-1\right)=\dfrac{19}{6}\)
\(\left(x-1\right)=\dfrac{19}{6}:2\)
\(x-1=\dfrac{19}{12}\)
\(x=\dfrac{19}{12}+1\)
\(x=\dfrac{31}{12}\)
Đúng 1
Bình luận (0)
\(\dfrac{7}{-2}x-\dfrac{1}{3}=-\dfrac{1}{2}\)
\(\dfrac{-7}{2}x-\dfrac{1}{3}=-\dfrac{1}{2}\)
\(\dfrac{-7}{2}x=\left(-\dfrac{1}{2}\right)+\dfrac{1}{3}\)
\(\dfrac{-7}{2}x=-\dfrac{1}{6}\)
\(x=\left(-\dfrac{1}{6}\right):\left(-\dfrac{7}{2}\right)\)
\(x=\dfrac{1}{21}\)
\(\dfrac{8}{5}-\dfrac{1}{2}:x=\dfrac{8}{3}\)
\(\dfrac{1}{2}:x=\dfrac{8}{5}-\dfrac{8}{3}\)
\(\dfrac{1}{2}:x=-\dfrac{16}{15}\)
\(x=\dfrac{1}{2}:\left(-\dfrac{16}{15}\right)\)
\(x=-\dfrac{15}{32}\)
\(-\dfrac{5}{4}x-\dfrac{1}{2}x=-\dfrac{7}{3}\)
\(x\cdot\left(-\dfrac{5}{4}-\dfrac{1}{2}\right)=-\dfrac{7}{3}\)
\(x\cdot\left(-\dfrac{7}{4}\right)=-\dfrac{7}{3}\)
\(x=\left(-\dfrac{7}{3}\right):\left(-\dfrac{7}{4}\right)\)
\(x=\dfrac{4}{3}\)
Đúng 0
Bình luận (0)
Chứng tỏ rằng:
a) 0,(37) + 0,(62) = 1
b) 0,(33) x 3 = 1
* 0,(37) = 0 phẩy chu kỳ 37
a) 0,(37)+0,(62) = 1
Có 0.(37)=\(\frac{37}{99}\)và 0.(62) = \(\frac{62}{99}\)
\(\frac{37}{99}\)+ \(\frac{62}{99}\)= 1
\(\Rightarrow0,\left(37\right)+0.\left(62\right)=1\)
b)\(0,\left(37\right)\times3=1\)
Có: \(0,\left(37\right)=\frac{37}{99}\)
\(\frac{37}{99}\times3=1\)
\(\Rightarrow0\left(37\right)\times3=1\)
Đúng 0
Bình luận (0)
1} Tính
A] 10(3) +0,(4) -8(6)
B] [ 12,3(1) -2,3(6) ] :4,(21)
2, tìm x biết
A] [ 0, (37 ) +0,(62) ] .x=10\
B] 0,(12) 1,(6) =x:0,(4)
Giups mình nhé thanks nhìu
bài 1:tìm hai số biết rằng khi viết thêm chữ số 0 vào bên phải số bé ta được số lớn và số lớn hơn số bé 9171 đơn vị
bài 2:tìm x
a)x+x*37+62*x=4000
b)(x+1)+(x+2)+(x+3)+(x+4)+(x+5)=65
trình bày đầy đủ nhanh mik tick cho
Bài 1:
Theo đề bài, khi viết chữ số 0 vào bên phải số bé ta được số lớn => số lớn gấp 10 lần số bé
Gọi số bé là a => số lớn là 10a
Theo đề bài, số lớn hơn số bé 9171 đơn vị => 10a - a = 9171 => 9a = 9171 => a = 1019
=> số bé là 1019, số lớn là 10190
Bài 2:
a) x + x*37 + 62*x= 4000
x*(1+37+62) = 4000
100x=4000
=> x=40
b) (x+1) + (x+2) + (x+3) + (x+4) + (x+5) = 65
=> 5x + 15 = 65
=> 5x = 50
=> x = 10
Đúng 0
Bình luận (0)



























