Tìm giá trị nhỏ nhất :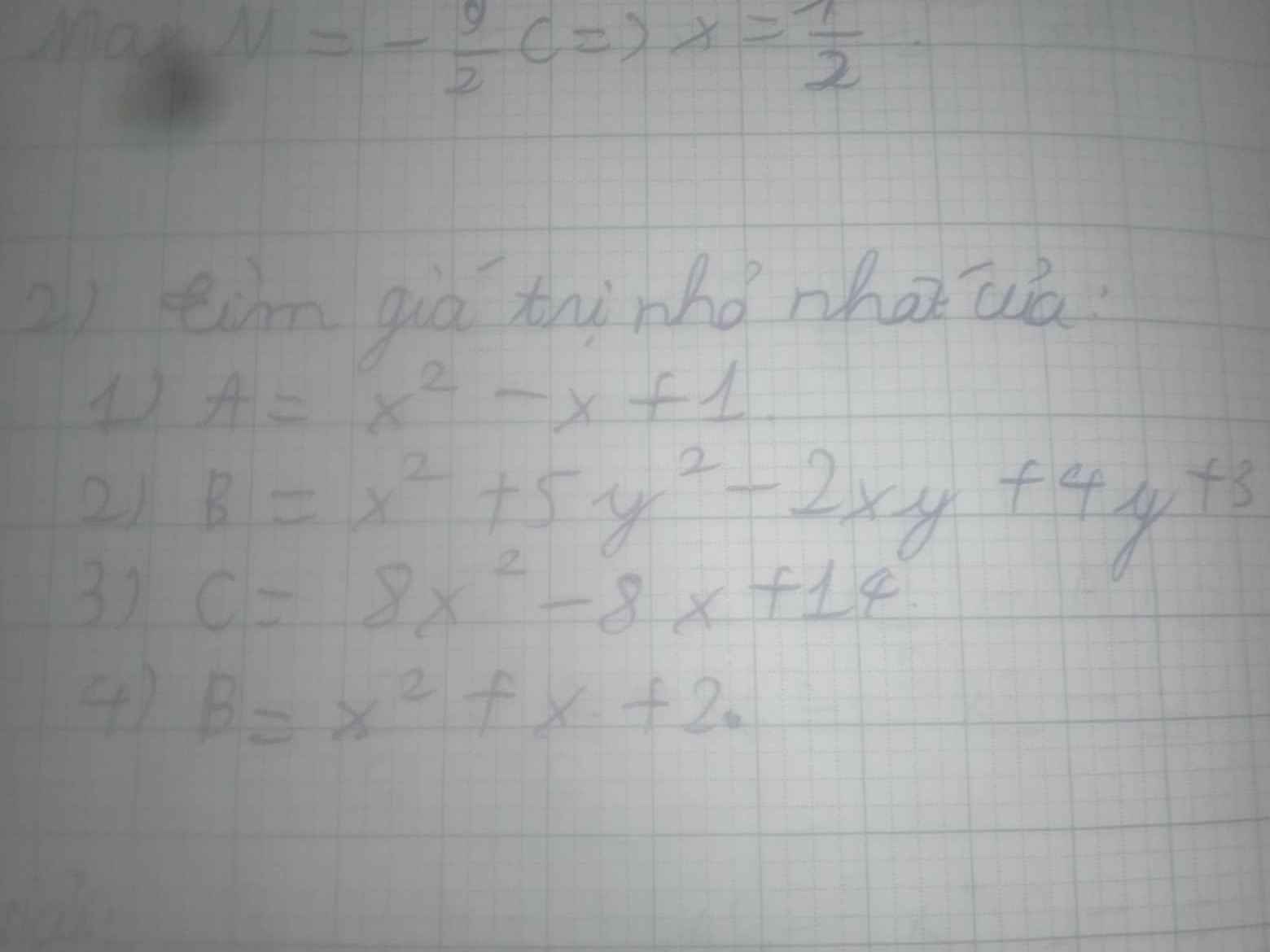

Những câu hỏi liên quan
tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số bạc hai y = -2x2 + 4x + 3
tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số bậc hai y = -3x2 + 2x + 1 trên (1;3)
tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số bậc hai y = x2 - 4x - 5 trên (-1;4)
Câu 1:
$y=-2x^2+4x+3=5-2(x^2-2x+1)=5-2(x-1)^2$
Vì $(x-1)^2\geq 0$ với mọi $x\in\mathbb{R}$ nên $y=5-2(x-1)^2\leq 5$
Vậy $y_{\max}=5$ khi $x=1$
Hàm số không có min.
Đúng 0
Bình luận (0)
Câu 2:
Hàm số $y$ có $a=-3<0; b=2, c=1$ nên đths có trục đối xứng $x=\frac{-b}{2a}=\frac{1}{3}$
Lập BTT ta thấy hàm số đồng biến trên $(-\infty; \frac{1}{3})$ và nghịch biến trên $(\frac{1}{3}; +\infty)$
Với $x\in (1;3)$ thì hàm luôn nghịch biến
$\Rightarrow f(3)< y< f(1)$ với mọi $x\in (1;3)$
$\Rightarrow$ hàm không có min, max.
Đúng 0
Bình luận (0)
Câu 3:
$y=x^2-4x-5$ có $a=1>0, b=-4; c=-5$ có trục đối xứng $x=\frac{-b}{2a}=2$
Do $a>0$ nên hàm nghịch biến trên $(-\infty;2)$ và đồng biến trên $(2;+\infty)$
Với $x\in (-1;4)$ vẽ BTT ta thu được $y_{\min}=f(2)=-9$
Đúng 0
Bình luận (0)
Cho biểu thức A=3/x-1
a. Tìm số nguyên x để A đạt giá trị nhỏ nhất. Tìm giá trị nhỏ nhất.
b. Tìm số nguyên x để A đạt giá trị lớn nhất. Tìm giá trị lớn nhất.
a) \(A=\dfrac{3}{x-1}\)
Điều kiện \(|x-1|\ge0\)
\(\Rightarrow A=\dfrac{3}{x-1}\ge0\)
\(GTNN\left(A\right)=0\) \(\Rightarrow x-1=+\infty\Rightarrow x\rightarrow+\infty\)
b) \(GTLN\left(A\right)\) không có \(\left(A=\dfrac{3}{x-1}\ge0\right)\)
Đúng 1
Bình luận (0)
Cho a={3;6;7} , b={0;23;29;6}
Tìm giá trị lớn nhất, giá trị nhỏ nhất Tìm giá trị lớn nhất giá trị nhỏ nhất của phân số a phần b
Câu 21. Cho và . Tính giá trị của biểu thức A. . B. . C. . D. .Câu 22. Tìm giá trị nhỏ nhất của .A. đạt giá trị nhỏ nhất là . B. đạt giá trị nhỏ nhất là C. đạt giá trị nhỏ nhất là . D. đạt giá trị nhỏ nhất là .Câu 23. Tìm giá trị lớn nhất của .A. đạt giá trị lớn nhất là . B. đạt giá trị lớn nhất là C. đạt giá trị lớn nhất là . D. đạt giá trị lớn nhất là /Câu 24. Tì...
Đọc tiếp
Câu 21. Cho ![]() và
và ![]() . Tính giá trị của biểu thức
. Tính giá trị của biểu thức ![]()
A. ![]() . B.
. B. ![]() . C.
. C. ![]() . D.
. D. ![]() .
.
Câu 22. Tìm giá trị nhỏ nhất của ![]() .
.
A. ![]() đạt giá trị nhỏ nhất là
đạt giá trị nhỏ nhất là ![]() . B.
. B. ![]() đạt giá trị nhỏ nhất là
đạt giá trị nhỏ nhất là ![]()
C. ![]() đạt giá trị nhỏ nhất là
đạt giá trị nhỏ nhất là ![]() . D.
. D. ![]() đạt giá trị nhỏ nhất là
đạt giá trị nhỏ nhất là ![]() .
.
Câu 23. Tìm giá trị lớn nhất của ![]() .
.
A. ![]() đạt giá trị lớn nhất là
đạt giá trị lớn nhất là ![]() . B.
. B. ![]() đạt giá trị lớn nhất là
đạt giá trị lớn nhất là ![]()
C. ![]() đạt giá trị lớn nhất là
đạt giá trị lớn nhất là ![]() . D.
. D. ![]() đạt giá trị lớn nhất là
đạt giá trị lớn nhất là ![]() /
/
Câu 24. Tìm ![]() thỏa mãn
thỏa mãn ![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
Câu 25. Hỏi có bao nhiêu giá trị ![]() thỏa mãn
thỏa mãn ![]() ?
?
A. Có một giá trị B. Có hai giá trị
C. Có ba giá trị D. Có bốn giá trị.
Tìm các giá trị của a ∈ N
a) PS dương \(\dfrac{2a-3}{4}\) có giá trị nhỏ nhất .Tìm giá trị nhỏ nhất đó
Lời giải:
Để PS $\frac{2a-3}{4}$ dương và có giá trị nhỏ nhất thì $2a-3>0$ và nhỏ nhất
Vì $2a-3$ nguyên nên $2a-3$ dương và có giá trị nhỏ nhất khi $2a-3=1$
$\Rightarrow a=2$
Vậy $\frac{2a-3}{4}$ nhỏ nhất bằng $\frac{1}{4}$
Đúng 0
Bình luận (0)
tìm giá trị nhỏ nhất của \(A=x^2-2x+5\)
tìm giá trị nhỏ nhất của \(B=2x^2-6x\)
tìm giá trị lớn nhất của \( C=4x-x^2+3\)
\(A=\left(x^2-2x+1\right)+4=\left(x-1\right)^2+4\ge4\\ A_{min}=4\Leftrightarrow x=1\\ B=2\left(x^2-3x\right)=2\left(x^2-2\cdot\dfrac{3}{2}x+\dfrac{9}{4}\right)-\dfrac{9}{2}\\ B=2\left(x-\dfrac{3}{2}\right)^2-\dfrac{9}{2}\ge-\dfrac{9}{2}\\ B_{min}=-\dfrac{9}{2}\Leftrightarrow x=\dfrac{3}{2}\\ C=-\left(x^2-4x+4\right)+7=-\left(x-2\right)^2+7\le7\\ C_{max}=7\Leftrightarrow x=2\)
Đúng 0
Bình luận (0)
a,\(A=x^2-2x+5=\left(x^2-2x+1\right)+4=\left(x-1\right)^2+4\ge4\)
Dấu "=" \(\Leftrightarrow x=-1\)
b,\(B=2\left(x^2-3x\right)=2\left(x^2-3x+\dfrac{9}{4}\right)-\dfrac{9}{2}=2\left(x-\dfrac{3}{2}\right)^2-\dfrac{9}{2}\ge-\dfrac{9}{2}\)
Dấu "=" \(\Leftrightarrow x=\dfrac{3}{2}\)
c,\(=C=-\left(x^2-4x-3\right)=-\left[\left(x^2-4x+4\right)-7\right]=-\left(x-2\right)^2+7\le7\)
Dấu "=" \(\Leftrightarrow x=2\)
Đúng 0
Bình luận (0)
a) Phân số -5n-9/6 có giá trị nhỏ nhất,tìm giá trị nhỏ nhất đó?
b) Phân số 7/4n-5 có giá trị lớn nhất, tìm giá trị lớn nhất đó?
Tìm giá trị của x và y để :
S = x + 2 + 2y –10 + 2011 đạt giá trị nhỏ nhất. Tìm giá trị nhỏ nhất đó .
Tìm giá trị nhỏ nhất của a và b để biểu thức C=a^2-4ab+5b^2-2b-6 có giá trị nhỏ nhất . Tìm giá trị nhỏ nhất đó.
C=a2-4ab+4b2+b2-2b+1-7=(a-2b)2+(b-1)2-7 > hoặc =-7
dấu = xảy ra khi a-2b=0
b-1=0
<=>a=2;b=1
..................................
a, Tìm x để A nhận giá trị lớn nhất, tìm giá trị lớn nhất để A = 1001 - I x+9 I
b, Tìm x để B nhận giá trị nhỏ nhất , tìm giá trị nhỏ nhất để B = I x-2I + 34























