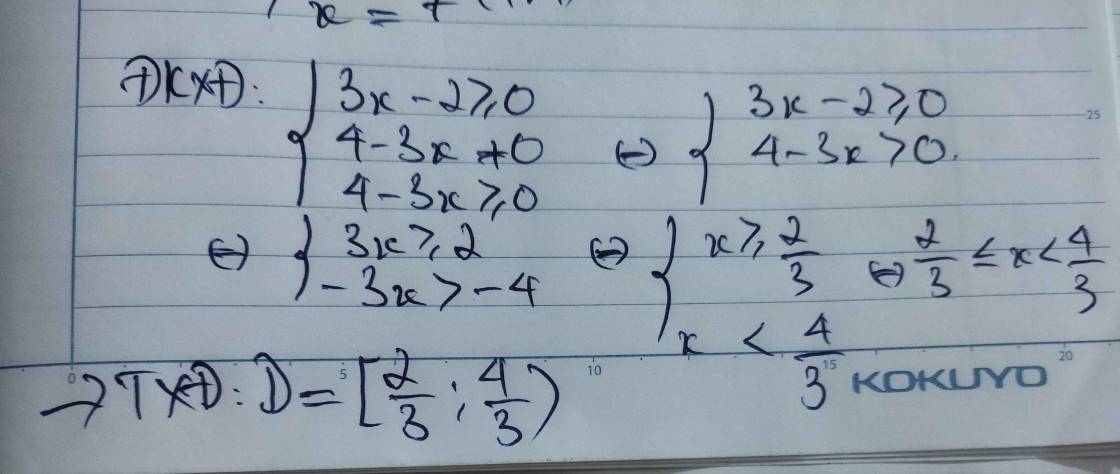tìm txđ

Những câu hỏi liên quan
Tìm TXĐ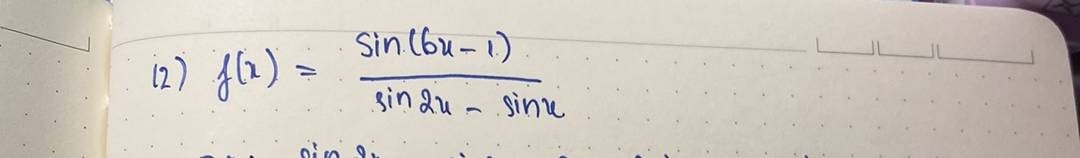
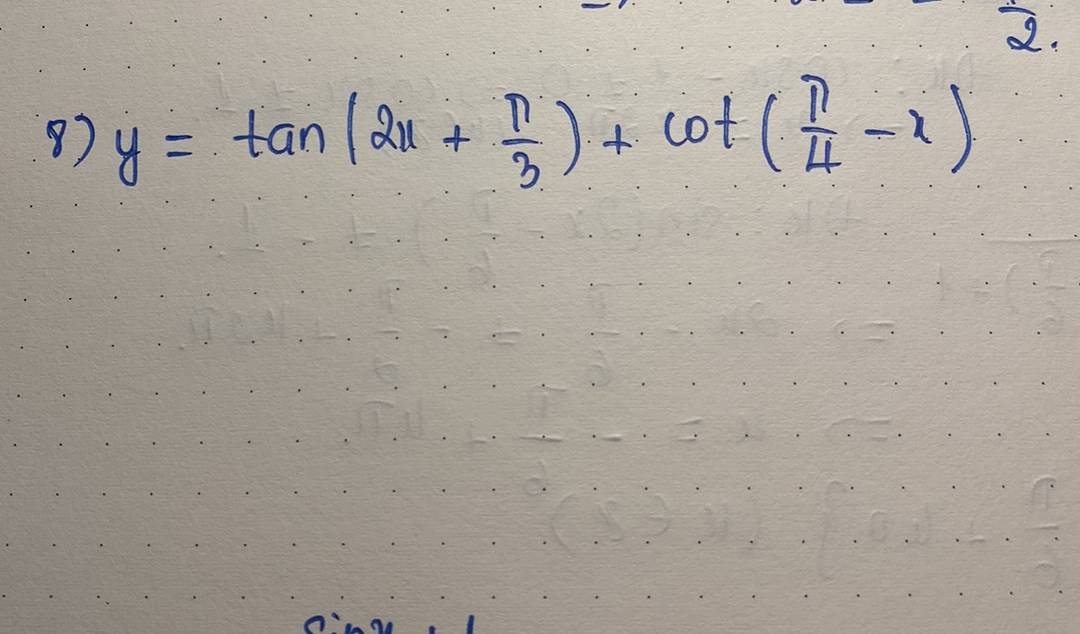
12: ĐKXĐ: sin 2x<>sin x
=>2x<>x+k2pi và 2x<>pi-x+k2pi
=>x<>k2pi và x<>pi/3+k2pi/3
Vậy: D=R\{k2pi;pi/3+k2pi/3}
8: ĐKXĐ: 2x+pi/3<>pi/2+kpi và pi/4-x<>kpi
=>2x<>pi/6+kpi và x<>pi/4-kpi
=>x<>pi/12+kpi/2 và x<>pi/4-kpi
Vậy: D=R\{pi/12+kpi/2;pi/4-kpi}
Đúng 0
Bình luận (0)
Tìm TXĐ của hàm số

ĐKXĐ:
a. \(\left\{{}\begin{matrix}x-1\ge0\\x^2-x-2\ne0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ge1\\x\ne2\end{matrix}\right.\)
b. \(\left\{{}\begin{matrix}x-1\ne0\\x>0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ne1\\x>0\end{matrix}\right.\)
c. \(\left\{{}\begin{matrix}2-x\ge0\\x+4>0\end{matrix}\right.\) \(\Leftrightarrow-4< x\le2\)
d. \(\left\{{}\begin{matrix}x-1\ge0\\\sqrt{x-1}\ne2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ge1\\x\ne5\end{matrix}\right.\)
e. \(\left\{{}\begin{matrix}3-x\ge0\\x^2-x\ne0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\le3\\x\ne0\\x\ne1\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Tìm TXĐ của hàm số sau
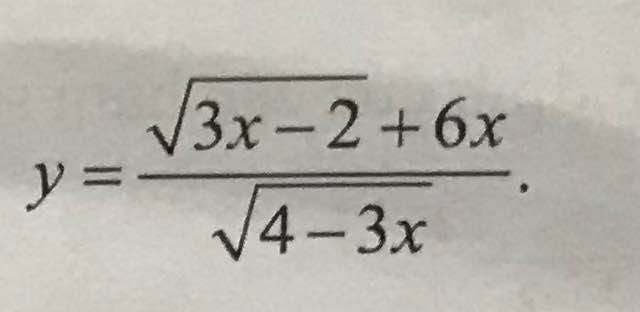
Tìm TXĐ:
\(\sqrt{\dfrac{1-Cosx}{2+2Sinx}}\)
ĐK: `(1-cosx)/(2+2sinx) >=0`
Có: `cosx<=1\ forall x => 1-cosx>=0\ forall x`
`-1<=sinx<=1<=>-2<=2sinx<=2<=>0<=2+2sinx<=4`
Hàm số xác định `<=> 2+2sinx \ne0 <=> sinx \ne -1 <=> x \ne -π/2+k2π\ (k in ZZ)`
Vậy `D=RR \\ {-π/2 +k2π ; k in ZZ}`
Đúng 0
Bình luận (0)
Tìm TXĐ của hàm số y=2cot(x+30°)
Hàm số xác định khi:
\(sin\left(x+30^o\right)\ne0\)
\(\Leftrightarrow x+30^o\ne k.180^o\)
\(\Leftrightarrow x\ne-30^o+k.180^o\)
Đúng 0
Bình luận (0)
tìm txđ của hàm số: y = 3 - cos2x/ tan2x
Hàm số \(y=3-\dfrac{cos2x}{tan2x}\) xác định khi \(\left\{{}\begin{matrix}sin2x\ne0\\cos2x\ne0\end{matrix}\right.\Leftrightarrow x\ne\dfrac{k\pi}{4}\).
Đúng 1
Bình luận (0)
a) Tìm TXĐ của biều thức. Với giá trị nào của x biểu thức vô nghĩa?
\(\dfrac{2-3x}{\dfrac{3x-2}{5}-\dfrac{x-4}{3}}\)
b) Tìm TXĐ của PT rồi giải PT:
\(\dfrac{3}{4x-20}\) + \(\dfrac{15}{50-2x^2}\) + \(\dfrac{7}{6x+30}\) = 0
a) Để biểu thức vô nghĩa thì \(\dfrac{3x-2}{5}-\dfrac{x-4}{3}=0\)
\(\Leftrightarrow\dfrac{3x-2}{5}=\dfrac{x-4}{3}\)
\(\Leftrightarrow3\left(3x-2\right)=5\left(x-4\right)\)
\(\Leftrightarrow9x-6=5x-20\)
\(\Leftrightarrow9x-5x=-20+6\)
\(\Leftrightarrow4x=-14\)
\(\Leftrightarrow x=-\dfrac{7}{2}\)
Đúng 0
Bình luận (0)
tìm txđ
\(y=log_2\left(\dfrac{x-3}{x+1}\right)\)
tìm txđ
\(y=log_2\left(x^2-2x\right)^{ }\)
\(y=\left(\dfrac{x+2}{x-2}\right)^{-2021}\)
ac giúp em với ạ
Đúng 0
Bình luận (0)
ĐKXĐ: \(\dfrac{x-3}{x+1}>0\)
\(\Leftrightarrow\left[{}\begin{matrix}x>3\\x< -1\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Tìm TXĐ của hàm số sau :
y = 1/sinx - 1/cos2x
Hàm số xác định \(\Leftrightarrow\left\{{}\begin{matrix}sinx\ne0\\cos2x\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}sinx\ne0\\tan^2x\ne1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ne k\pi\\x\ne\dfrac{\pi}{4}+k\pi\\x\ne-\dfrac{\pi}{4}+k\pi\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ne k\pi\\x\ne\dfrac{\pi}{4}+\dfrac{k\pi}{2}\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Tìm txđ của hàm số sau:\(y=\dfrac{x}{sinx+tanx}\)
ĐKXĐ: \(\left\{{}\begin{matrix}cosx\ne0\\sinx+tanx\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}cosx\ne0\\\dfrac{sinx\left(1+cosx\right)}{cosx}\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}cosx\ne0\\sinx\ne0\end{matrix}\right.\)
\(\Leftrightarrow sin2x\ne0\)
\(\Rightarrow2x\ne k\pi\Rightarrow x\ne\dfrac{k\pi}{2}\)
Đúng 0
Bình luận (0)