Giải pt giúp e vs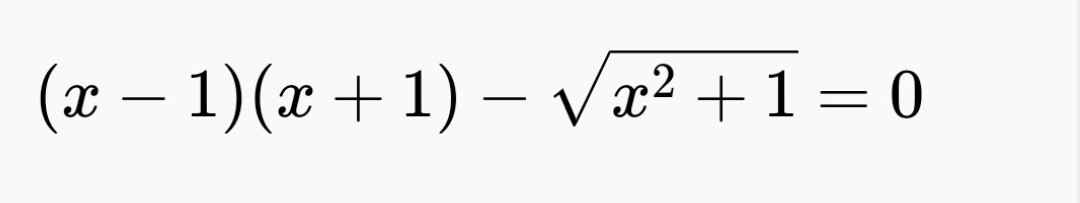

Những câu hỏi liên quan
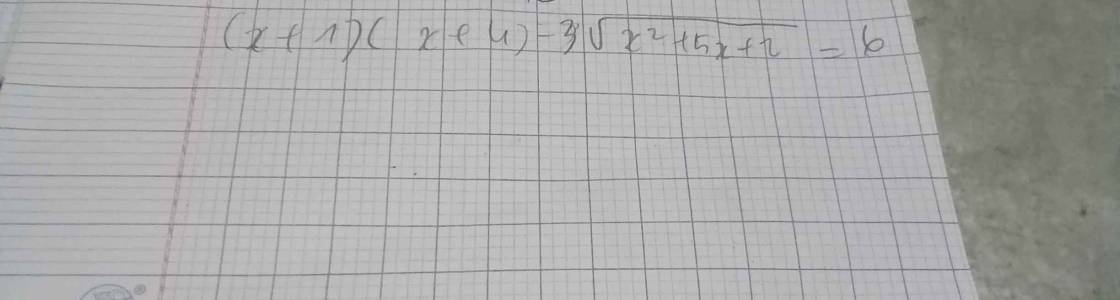 giải pt này giúp e vs ạ
giải pt này giúp e vs ạ
ĐKXĐ: \(x^2+5x+2>=0\)
=>\(\left[{}\begin{matrix}x>=\dfrac{-5+\sqrt{17}}{2}\\x< =\dfrac{-5-\sqrt{17}}{2}\end{matrix}\right.\)
\(\left(x+1\right)\left(x+4\right)-3\sqrt{x^2+5x+2}=6\)
=>\(x^2+5x+4-3\sqrt{x^2+5x+2}-6=0\)
=>\(x^2+5x+2-3\sqrt{x^2+5x+2}-4=0\)(1)
Đặt \(\sqrt{x^2+5x+2}=a\)(a>=0)
Phương trình (1) trở thành:
\(a^2-3a-4=0\)
=>(a-4)(a+1)=0
=>\(\left[{}\begin{matrix}a=4\left(nhận\right)\\a=-1\left(loại\right)\end{matrix}\right.\)
=>\(x^2+5x+2=4^2=16\)
=>\(x^2+5x-14=0\)
=>\(\left(x+7\right)\left(x-2\right)=0\)
=>\(\left[{}\begin{matrix}x=-7\left(nhận\right)\\x=2\left(nhận\right)\end{matrix}\right.\)
Đúng 1
Bình luận (0)
2sin^2.2x-3cos2x+6sin^2-9=0. Giúp e giải pt này vs ạ
Đề là: \(2sin^22x-3cos2x+6sin^2x-9=0\) đúng không nhỉ?
\(\Leftrightarrow2\left(1-cos^22x\right)-3cos2x+3\left(1-cos2x\right)-9=0\)
\(\Leftrightarrow-2cos^22x-6cos2x-4=0\)
\(\Leftrightarrow cos^22x+3cos2x+2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos2x=-1\\cos2x=-2\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow...\)
Đúng 1
Bình luận (0)
Giúp e vs ạ Giải bất pt: a) 2x - x(3x + 1) < 15 - 3x(x + 2) b) 4(x - 3)² - (2x - 1)² ≥ 12x
a: =>2x-3x^2-x<15-3x^2-6x
=>x<-6x+15
=>7x<15
=>x<15/7
b: =>4x^2-24x+36-4x^2+4x-1>=12x
=>-20x+35>=12x
=>-32x>=-35
=>x<=35/32
Đúng 0
Bình luận (0)
\(a,2x-x\left(3x+1\right)< 15-3x\left(x+2\right)\\ \Leftrightarrow2x-3x^2-x< 15-3x^2-6x\\ \Leftrightarrow3x^2-3x^2+2x+6x-x< 15\\ \Leftrightarrow7x< 15\\ \Leftrightarrow x< \dfrac{15}{7}\)
Vậy S={-∞; 15/7}
Đúng 1
Bình luận (2)
\(b,4\left(x-3\right)^2-\left(2x-1\right)^2\ge12x\\ \Leftrightarrow4\left(x^2-6x+9\right)-\left(4x^2-4x+1\right)-12x\ge0\\ \Leftrightarrow4x^2-4x^2-24x+4x-12x\ge-36+1\\ \Leftrightarrow-32x\ge-35\\ \Leftrightarrow x\le\dfrac{35}{32}\)
Vậy S={-∞; 35/32]
Đúng 1
Bình luận (1)
M.n ơi giải giúp mìn bài 2 .3 câu giải bất pt và hệ bất pt vs tí nx mìn thi rồi .giúp mìn vs
\(\left\{{}\begin{matrix}3x+1< x-7\\1-2x>x+1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}2x< -8\\3x< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x< -4\\x< 0\end{matrix}\right.\) \(\Rightarrow x< -4\)
Vậy nghiệm của hệ là \(S=\left(-\infty;-4\right)\)
Đúng 0
Bình luận (0)
giúp e vs mn :( giải pt
6x4-x3-7x2+x+1=0
cái này bạn cố gắng phân tích ra đi
Đúng 0
Bình luận (0)
6x4 - x3 - 7x2 + x + 1 = 0
=> (x + 1)(3x + 1)(x - 1)(2x - 1) = 0
=> x + 1 = 0 => x = -1
hoặc 3x + 1 = 0 => x = -1/3
hoặc x - 1 = 0 => x = 1
hoặc 2x - 1 = 0 => x = 1/2
Vậy x = -1, x = -1/3, x = 1 , x = 1/2
Đúng 0
Bình luận (0)
1)Cos^2(x-pi/5)=sin^2(2x+4pi/5) 2)sin3x=căn2.cos(x-pi/5)+cos3x Giúp e các bước giải 2 pt này vs ạ
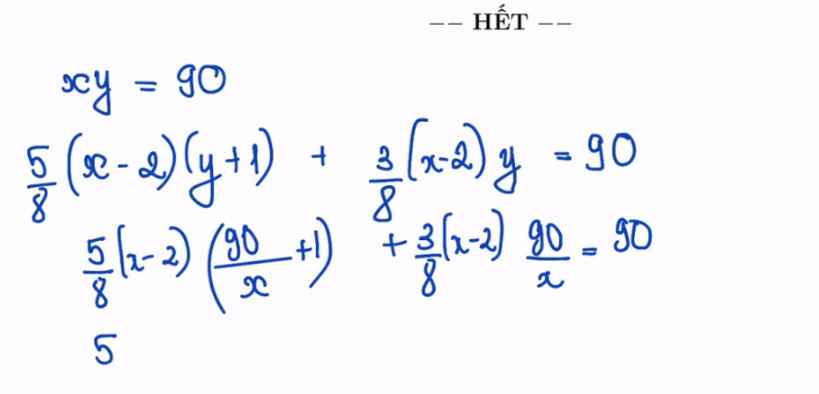
giải hộ e pt vs ạ
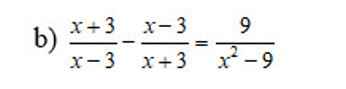
giải giúp pt này vs mn
\(\dfrac{x+3}{x-3}-\dfrac{x-3}{x+3}=\dfrac{9}{x^2-9}\left(ĐKXĐ:x\ne\pm3\right)\)
\(\Leftrightarrow\dfrac{\left(x+3\right)^2-\left(x-3\right)^2}{\left(x-3\right)\left(x+3\right)}=\dfrac{9}{\left(x-3\right)\left(x+3\right)}\)
\(\Rightarrow x^2+6x+9-x^2+6x-9=9\)
\(\Leftrightarrow12x=9\)
\(\Leftrightarrow x=\dfrac{3}{4}\) (nhận).
Vậy \(S=\left\{\dfrac{3}{4}\right\}\)
Đúng 4
Bình luận (0)
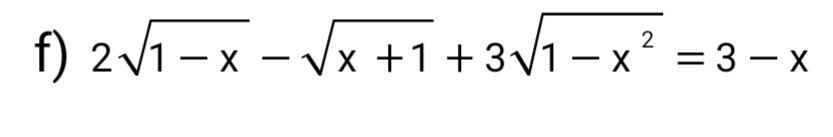 Giải pt . Mn giúp mik vs
Giải pt . Mn giúp mik vs
ĐK: \(-1\le x\le1\)
Đặt \(\sqrt{1-x}=a;\sqrt{x+1}=b\Rightarrow3-x=2a^2+b^2\)
\(pt\Leftrightarrow2a-b+3ab=2a^2+b^2\)
\(\Leftrightarrow2a^2+b^2-2a+b-3ab=0\)
\(\Leftrightarrow2a^2-a\left(3b+2\right)+b^2+b=0\)
\(\Delta=\left(3b+2\right)^2-4.2.\left(b^2+b\right)=9b^2+12b+4-8b^2-8b\)
\(=b^2+4b+4=\left(b+2\right)^2\)
\(\Rightarrow\left[{}\begin{matrix}a=\dfrac{3b+2-\left(b+2\right)}{4}=\dfrac{2b}{4}=\dfrac{b}{2}\Leftrightarrow2a=b\left(1\right)\\a=\dfrac{3b+2+b+2}{4}=\dfrac{4b+4}{4}=b+1\left(2\right)\end{matrix}\right.\)
pt (1) \(\Leftrightarrow2\sqrt{1-x}=\sqrt{x+1}\)
\(\Leftrightarrow4\left(1-x\right)=x+1\)
\(\Leftrightarrow5x=3\Leftrightarrow x=\dfrac{5}{3}\left(tm\right)\)
\(pt\left(2\right)\Leftrightarrow\sqrt{1-x}=1+\sqrt{x+1}\)
\(\Leftrightarrow1-x=1+x+1+2\sqrt{x+1}\)
\(\Leftrightarrow-1-2x=2\sqrt{x+1}\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\le-\dfrac{1}{2}\\4x^2+4x+1=4x+4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\le-\dfrac{1}{2}\\4x^2=3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\le-\dfrac{1}{2}\\\left[{}\begin{matrix}x=\dfrac{\sqrt{3}}{2}\left(l\right)\\x=-\dfrac{\sqrt{3}}{2}\left(tm\right)\end{matrix}\right.\end{matrix}\right.\)
Vậy, pt có tập nghiệm là: \(S=\left\{-\dfrac{\sqrt{3}}{2};\dfrac{5}{3}\right\}\)
Đúng 1
Bình luận (0)
Giúp e câu 2 vs ạ :( Cho pt: 4x


















