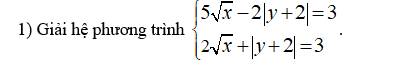\(\Leftrightarrow x^2-1=\sqrt{x^2+1}\\ \Leftrightarrow x^4-2x^2+1=x^2+1\\ \Leftrightarrow x^4-3x^2=0\\ \Leftrightarrow x^2\left(x^2-3\right)=0\\ \Rightarrow\left[{}\begin{matrix}x=0\left(l\right)\\x=\sqrt{3}\left(n\right)\\x=-\sqrt{3}\left(n\right)\end{matrix}\right.\)
Vậy \(S=\left\{\pm\sqrt{3}\right\}\)

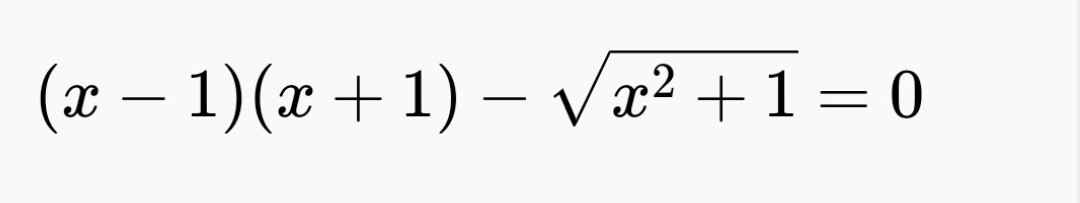




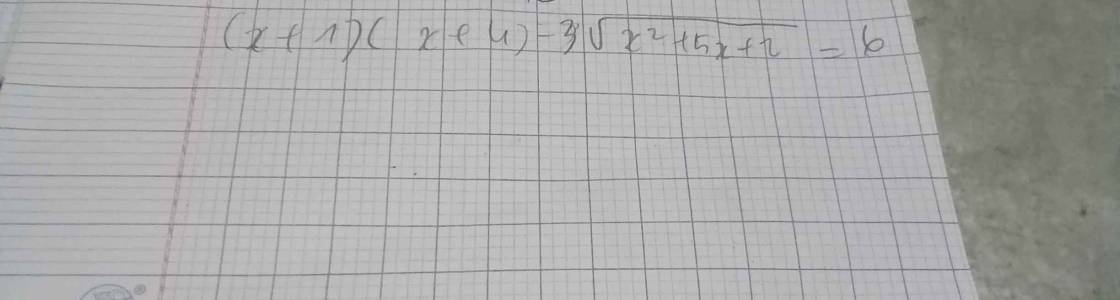

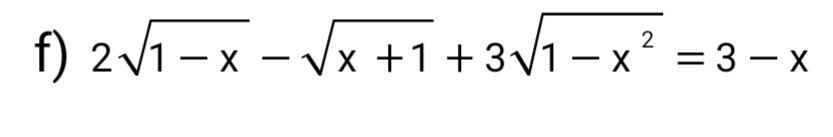 Giải pt . Mn giúp mik vs
Giải pt . Mn giúp mik vs