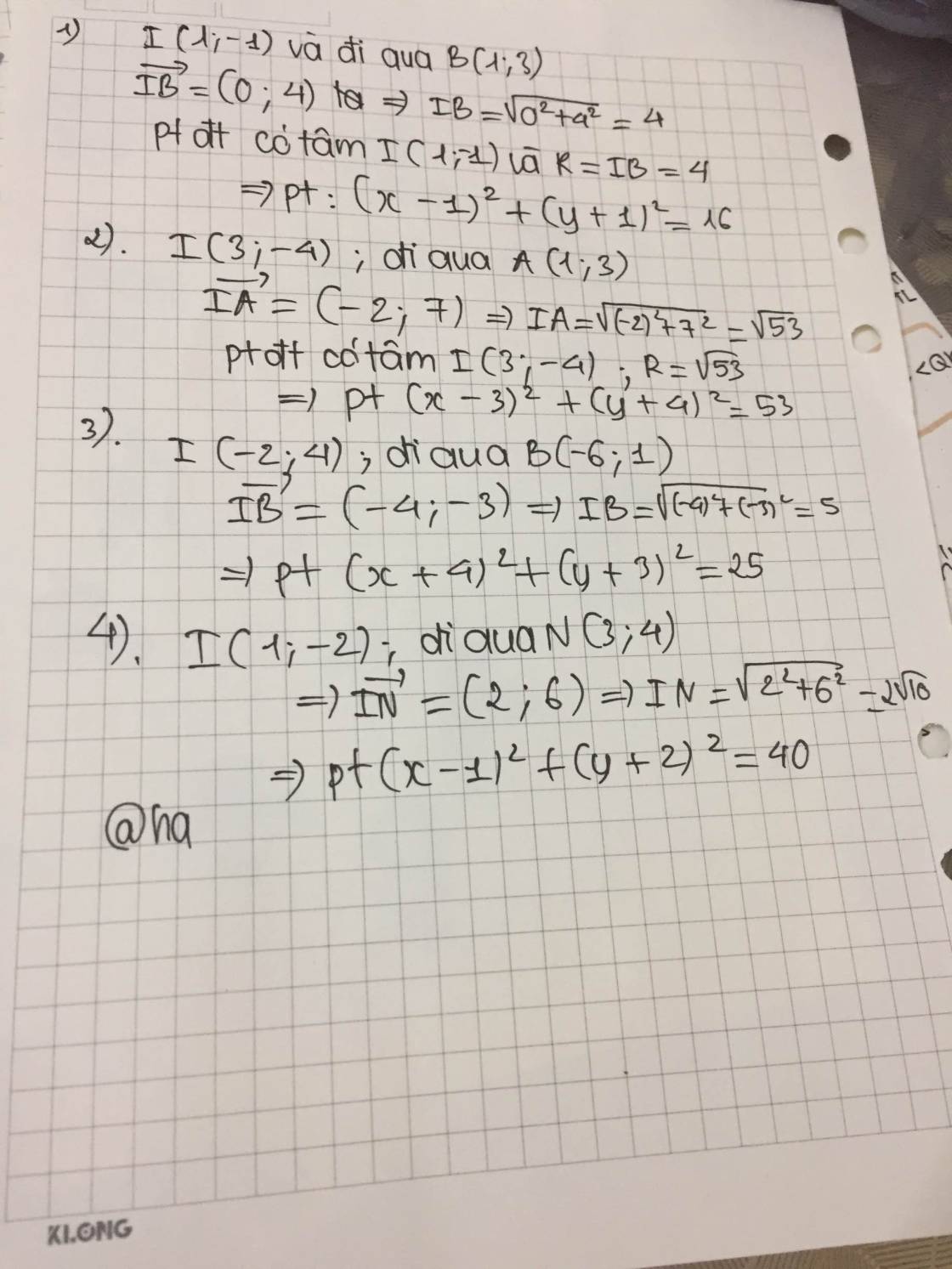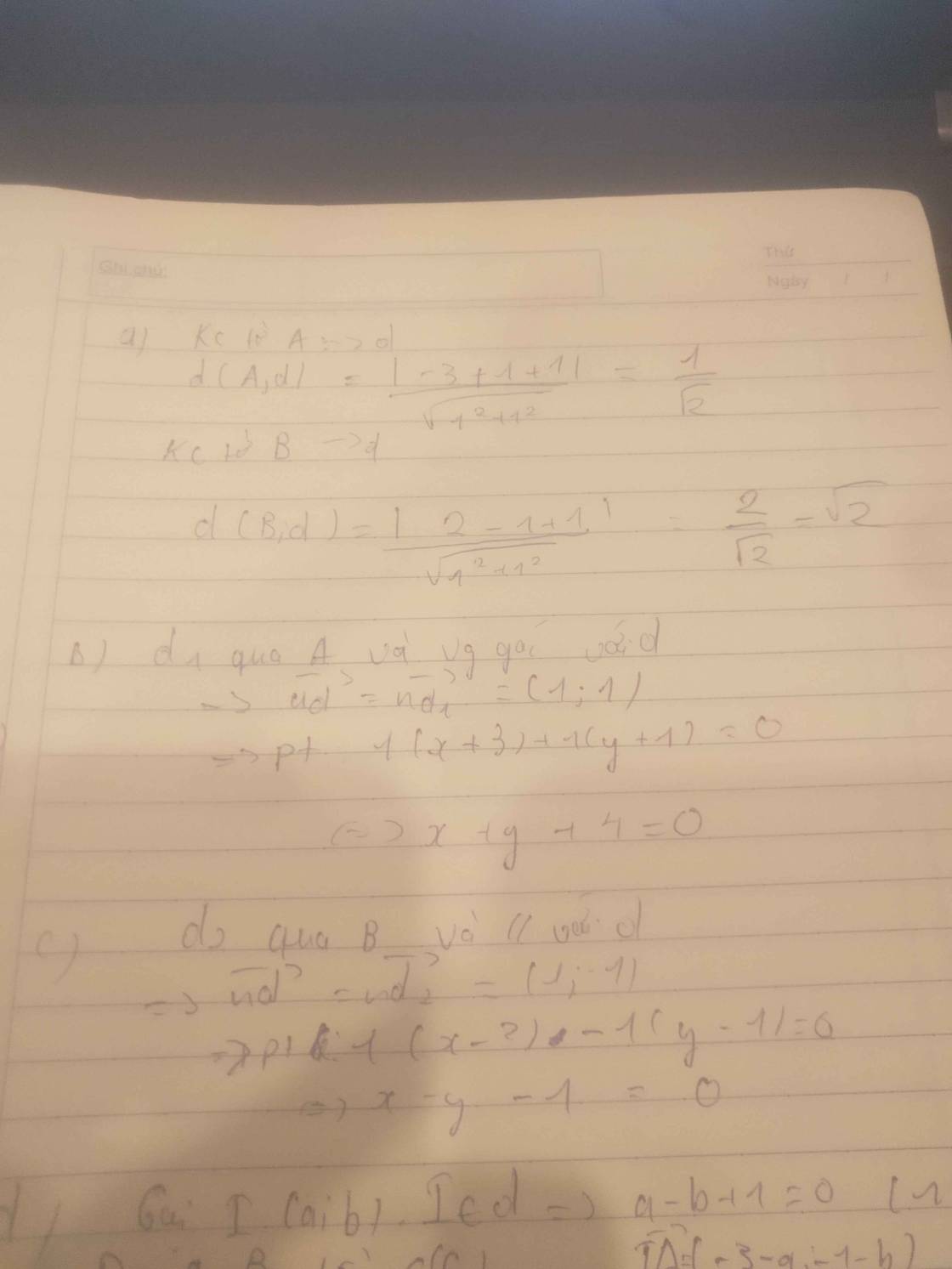a.

\(R=d\left(A;d\right)=\dfrac{\left|3+1-2\right|}{\sqrt{1^2+1^2}}=\sqrt{2}\)

Phương trình đường tròn:

\(\left(x-3\right)^2+\left(y-1\right)^2=2\)

b.

Tiếp tuyến d' qua O nên có dạng: \(ax+by=0\)

d' tiếp xúc (C) nên \(d\left(A;d'\right)=R\)

\(\Leftrightarrow\dfrac{\left|3a+b\right|}{\sqrt{a^2+b^2}}=\sqrt{2}\Leftrightarrow\left(3a+b\right)^2=2a^2+2b^2\)

\(\Leftrightarrow7a^2+6ab-b^2=0\Rightarrow\left(a+b\right)\left(7a-b\right)=0\)

\(\Rightarrow\left[{}\begin{matrix}a+b=0\\7a-b=0\end{matrix}\right.\) chọn \(\left[{}\begin{matrix}\left(a;b\right)=\left(1;-1\right)\\\left(a;b\right)=\left(1;7\right)\end{matrix}\right.\)

Có 2 tiếp tuyến thỏa mãn: \(\left[{}\begin{matrix}x-y=0\\x+7y=0\end{matrix}\right.\)

c.

Gọi M là trung điểm EF

\(\Rightarrow AM\perp EF\Rightarrow AM=d\left(A;d\right)=\sqrt{2}\)

\(S_{AEF}=\dfrac{1}{2}AM.EF=6\Rightarrow AM.EF=12\)

\(\Rightarrow EF=\dfrac{12}{\sqrt{2}}=6\sqrt{2}\)

\(\Rightarrow EM=\dfrac{EF}{2}=3\sqrt{2}\)

Áp dụng Pitago:

\(R'=AE=\sqrt{EM^2+AM^2}=2\sqrt{5}\)

a: \(IA=\sqrt{\left(-2-1\right)^2+\left(0+2\right)^2}=\sqrt{13}\)

Phương trình (C) là:

(x-1)^2+(y+2)^2=13

b: vecto IM=(3;2)

Phương trình tiếp tuyến là:

3(x-4)+2(y-0)=0

=>3x+2y-12=0

\(CA=\sqrt{\left(2-1\right)^2+\left(-5-1\right)^2}=\sqrt{37}\)

\(CB=\sqrt{\left(2-0\right)^2+\left(-5-3\right)^2}=2\sqrt{17}\)

Vì CA<>CB

nên ko có đường tròn tâm C có A,B thuộc đường tròn đó

  d lâu r ko làm ko nhớ -)(

a.

Ta có: \(\left\{{}\begin{matrix}-4a=-2\\8b=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=2\\b=-4\end{matrix}\right.\) \(\Rightarrow I\left(2;-4\right)\)

\(R=\sqrt{2^2+\left(-4\right)^2+5}=5\)

b.

PTTT: \(\left(C\right):\left(a-x_0\right)\left(x-x_0\right)+\left(b-y_0\right)\left(y-y_0\right)=0\)

\(\Leftrightarrow\left(2+1\right)\left(x+1\right)+\left(-4-0\right)\left(y-0\right)=0\)

\(\Leftrightarrow\left(C\right):3x-4y=-3\)

c.

Ta có: \(\Delta\perp d\Rightarrow\Delta:4x+3y+c=0\)

\(d\left(I,\Delta\right):\dfrac{\left|4\cdot2-3\cdot4+c\right|}{\sqrt{4^2+3^2}}=5\)

\(\Leftrightarrow\left|c-4\right|=25\) \(\Leftrightarrow\left[{}\begin{matrix}c=29\\c=-21\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}\Delta:4x+3y+29=0\\\Delta:4x+3y-21=0\end{matrix}\right.\)

1.

Gọi \(I\left(x;y\right)\) là tâm đường tròn \(\Rightarrow\overrightarrow{AI}=\left(x-1;y-3\right)\)

Do đường tròn tiếp xúc với \(d_1;d_2\) nên:

\(d\left(I;d_1\right)=d\left(I;d_2\right)\Rightarrow\dfrac{\left|5x+y-3\right|}{\sqrt{26}}=\dfrac{\left|2x-7y+1\right|}{\sqrt{53}}\)

Chà, đề đúng ko em nhỉ, thế này thì vẫn làm được nhưng rõ ràng nhìn 2 cái mẫu kia thì số liệu sẽ xấu 1 cách vô lý.

2.

Phương trình đường thẳng kia là gì nhỉ? \(2x+y=0\) à?