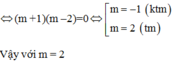Tìm m để: 2x2 + (m - 6)x - m2 - 3m = 0 có 2 nghiệm phân biệt x1, x2 thoả mãn: 1<x1<x2

Những câu hỏi liên quan
Tìm m để: 2x2 + (m - 6)x - m2 - 3m = 0 có 2 nghiệm phân biệt x1, x2 thoả mãn: 1
Cho phương trình: x2 – (2m+1)x + m2 + m -2 0 (1) (m là tham số). Tìm m để phương trình (1) có 2 nghiệm phân biệt x1, x2 thoả mãn: x1(x1 -2x2) + x2(x2 -3x1) 9
Đọc tiếp
Cho phương trình: x2 – (2m+1)x + m2 + m -2 = 0 (1) (m là tham số). Tìm m để phương trình (1) có 2 nghiệm phân biệt x1, x2 thoả mãn:
x1(x1 -2x2) + x2(x2 -3x1) = 9
\(\Delta=\left(2m+1\right)^2-4\left(m^2+m-2\right)=9>0;\forall m\)
Phương trình luôn có 2 nghiệm pb với mọi m
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2m+1\\x_1x_2=m^2+m-2\end{matrix}\right.\)
\(x_1\left(x_1-2x_2\right)+x_2\left(x_2-2x_1\right)=9\)
\(\Leftrightarrow x_1^2+x_2^2-4x_1x_2=9\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-6x_1x_2=9\)
\(\Leftrightarrow\left(2m+1\right)^2-6\left(m^2+m-4\right)=9\)
\(\Leftrightarrow2m^2+2m-4=0\)
\(\Rightarrow\left[{}\begin{matrix}m=1\\m=-2\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Cho phương trình x2 - 2(m + 1) + m2 + 1 = 0, với m là tham số. Tìm các giá trị của m để phương trình có 2 nghiệm phân biệt x1, x2 (x1<x2) thoả mãn :
(2x2 - 3)2 - (2x2 - 3)2 = 32m - 16
Tìm m để phương trình x^2 − 2m x + m - 3 = 0 có hai nghiệm phân biệt x1, x2 thoả mãn (x1-2x2)^2+x2-2mx1=20
Cho pt x2 -(m-2)x-m2 +3m-4=0 (*)
a, Giải (*) khi m =0
b) CM pt có hai nghiệm trái dấu vs mọi m
c, Tìm m để pt (*) có nghiệm x1 x2 thoả mãn (x1+2x2)(x2+2x1)
chủ yếu là hỏi câu c hả? tớ làm mỗi đoạn đưa về tổng - tích thôi, bạn giải thấy khó chỗ nào thì hỏi cụ thể nhe ^^
\(\left(x_1+2x_2\right)\left(x_2+2x_1\right)=x_1x_2+2x_2^2+2x_1^2+4x_1x_2=2\left(x_1+x_2\right)^2-4x_1x_2+5x_1x_2\)
đến đây Vi-ét đc òi
Đúng 0
Bình luận (0)
Gotcha Tokoyami
Có \(\Delta=\left(m-2\right)^2-4\left(-m^2+3m-4\right)\)
\(=m^2-4m+4+4m^2-12m+16\)
\(=5m^2-16m+20\)
\(=5\left(m^2-\frac{16}{5}m+4\right)\)
\(=5\left[\left(m^2-2.\frac{8}{5}m+\frac{64}{25}\right)+\frac{36}{25}\right]\)
\(=5\left[\left(m-\frac{8}{5}\right)^2+\frac{36}{25}\right]>0\forall m\)
Nên pt có 2 nghiệm phân biệt với mọi m
a, Với m = 0 thì pt trở thành
\(x^2+2x-4=0\)
Có \(\Delta'=1+4=5>0\)
\(\Rightarrow\orbr{\begin{cases}x=-1+\sqrt{5}\\x=-1-\sqrt{5}\end{cases}}\)
b, Theo hệ thức Vi-et \(x_1x_2=-m^2+3m-4=-\left(m-\frac{3}{2}\right)^2-\frac{7}{4}< 0\)
nên pt có 2 nghiệm trái dấu
c, Thiếu đề , nhưng làm hộ 1 bước biến đổi như bạn dưới
Đúng 0
Bình luận (0)
Tìm m để: x2 - 2x - m2 - 2m = 0 có 2 nghiệm phân biệt x1, x2 thoả mãn: x1<2<x2
có :
\(\Delta'=1^2-\left(-m^2+1\right)=m^2\)
pt có \(2\) nghiệm phân biệt \(\Leftrightarrow m^2>0\Leftrightarrow m\ne0\)
\(\Rightarrow x_1=2+m;x_2=2-m\)
theo đề :
\(x_2=x^2_1\Leftrightarrow2-m=\left(2+m\right)^2\)
\(\Leftrightarrow\left(m=\dfrac{-5+\sqrt{17}}{2}\left(ktm\right)\right);\left(m=\dfrac{-5-\sqrt{17}}{2}\left(ktm\right)\right)\)
vậy không có \(m\) thỏa mãn
Đúng 3
Bình luận (0)
tìm các giá trị của tham số m để phương trình x2-2(m-1)x+m2=0 có hai nghiệm phân biệt x1,x2 thỏa mãn hệ thức (x1-x2)2+6m = x1-2x2
Cho phương trình x2 - 2(m + 3)x + m2 + 3 = 0 Tìm m để phương trình có hai nghiệm phân biệt x1, x2 thỏa mãn (2x1 - 1)(2x2 - 1) = 9
Cho phương trình:
x
2
– 2(m – 1)x +
m
2
− 3m 0. Tìm m để phương trình có 2 nghiệm phân biệt
x
1
;
x
2
thỏa mãn
x
1
2
+
x
2
2
8
A. m 2 B....
Đọc tiếp
Cho phương trình: x 2 – 2(m – 1)x + m 2 − 3m = 0. Tìm m để phương trình có 2 nghiệm phân biệt x 1 ; x 2 thỏa mãn x 1 2 + x 2 2 = 8
A. m = 2
B. m = −1
C. m = −2
D. m = 1