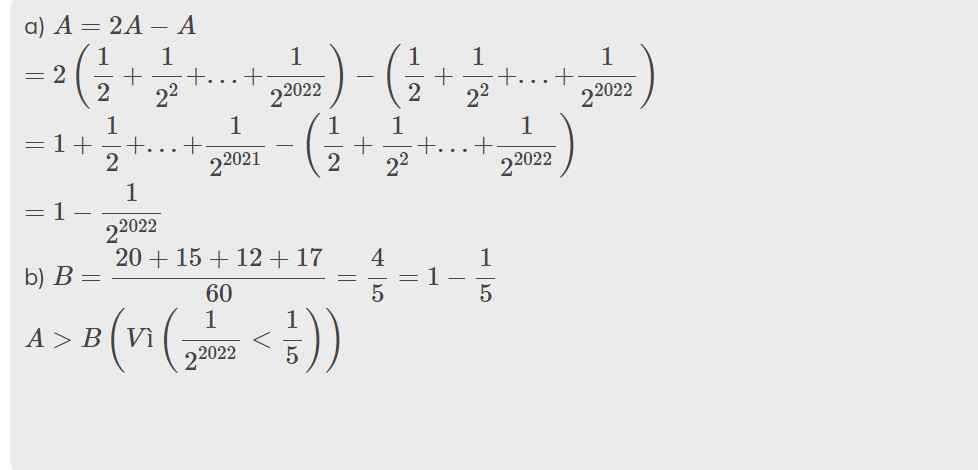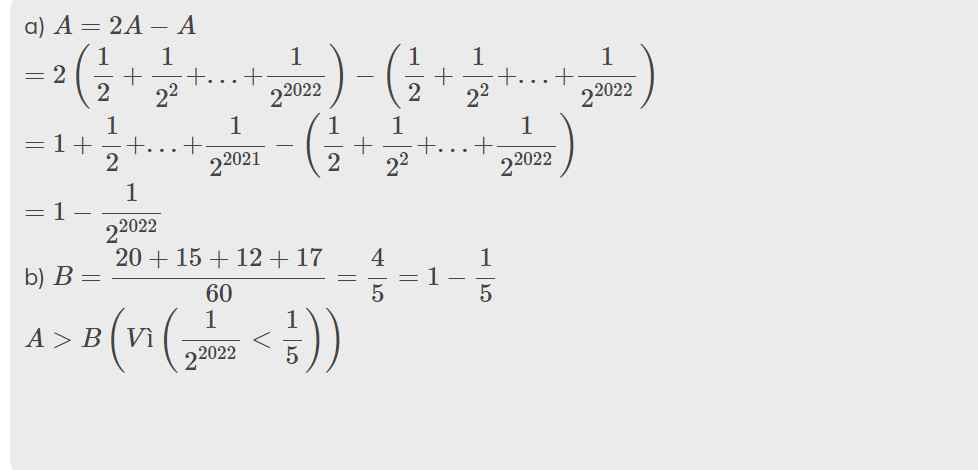`#3107`

\(A=1+2^1+2^2+2^3+...+2^{2015}\)

\(2A=2+2^2+2^3+2^4+...+2^{2016}\)

\(2A-A=\left(2+2^2+2^3+2^4+...+2^{2016}\right)-\left(1+2+2^2+2^3+...+2^{2015}\right)\)

\(A=2+2^2+2^3+2^4+...+2^{2016}-1-2-2^2-2^3-...-2^{2015}\)

\(A=2^{2016}-1\)

Vậy, \(A=2^{2016}-1.\)

\(A=2^0+2^1+2^2+...+2^{2015}\)

\(2\cdot A=2^1+2^2+2^3+...+2^{2016}\)

\(A=2A-A=2^{2016}-2^0\)

\(A=2^{2016}-1\)

a) \(A=1+2+2^2+...+2^{80}\)

\(2A=2+2^2+2^3+...+2^{81}\)

\(2A-A=2+2^2+2^3+...+2^{81}-1-2-2^2-...-2^{80}\)

\(A=2^{81}-1\)

Nên A + 1 là:

\(A+1=2^{81}-1+1=2^{81}\)

b) \(B=1+3+3^2+...+3^{99}\)

\(3B=3+3^2+3^3+...+3^{100}\)

\(3B-B=3+3^2+3^3+...+3^{100}-1-3-3^2-...-3^{99}\)

\(2B=3^{100}-1\)

Nên 2B + 1 là:

\(2B+1=3^{100}-1+1=3^{100}\)

2) 

a) \(2^x\cdot\left(1+2+2^2+...+2^{2015}\right)+1=2^{2016}\)

Gọi:

\(A=1+2+2^2+...+2^{2015}\)

\(2A=2+2^2+2^3+...+2^{2016}\)

\(A=2^{2016}-1\)

Ta có:

\(2^x\cdot\left(2^{2016}-1\right)+1=2^{2016}\)

\(\Rightarrow2^x\cdot\left(2^{2016}-1\right)=2^{2016}-1\)

\(\Rightarrow2^x=\dfrac{2^{2016}-1}{2^{2016}-1}=1\)

\(\Rightarrow2^x=2^0\)

\(\Rightarrow x=0\)

b) \(8^x-1=1+2+2^2+...+2^{2015}\)

Gọi: \(B=1+2+2^2+...+2^{2015}\)

\(2B=2+2^2+2^3+...+2^{2016}\)

\(B=2^{2016}-1\)

Ta có:

\(8^x-1=2^{2016}-1\)

\(\Rightarrow\left(2^3\right)^x-1=2^{2016}-1\)

\(\Rightarrow2^{3x}-1=2^{2016}-1\)

\(\Rightarrow2^{3x}=2^{2016}\)

\(\Rightarrow3x=2016\)

\(\Rightarrow x=\dfrac{2016}{3}\)

\(\Rightarrow x=672\)

Ta có: \(A=1+2+2^2+...+2^{2015}\)

\(2A=2\cdot\left(1+2+2^2+...+2^{2015}\right)\)

\(2A=2+2^2+2^3+...+2^{2016}\)

\(2A-A=2+2^2+...+2^{2016}-1-2-2^2-...-2^{2015}\)

\(A=2^{2016}-1\)

A không thể biết dưới dạng lũy thừa của 8 được 

A=22016−1

giải ròi đó nhoa

1/

Tổng A là tổng các số hạng cách đều nhau 4 đơn vị.

Số số hạng: $(101-1):4+1=26$

$A=(101+1)\times 26:2=1326$

2/

$B=(1+2+2^2)+(2^3+2^4+2^5)+(2^6+2^7+2^8)+(2^9+2^{10}+2^{11})$

$=(1+2+2^2)+2^3(1+2+2^2)+2^6(1+2+2^2)+2^9(1+2+2^2)$

$=(1+2+2^2)(1+2^3+2^6+2^9)$

$=7(1+2^3+2^6+2^9)\vdots 7$

3/
$C=1+2+2^2+2^3+...+2^{99}$

$2C=2+2^2+2^3+2^4+...+2^{100}$

$\Rightarrow 2C-C=2^{100}-1$

$\Rightarrow C=2^{100}-1$

\(A=1+2^1+2^2+...+2^{2015}\)

\(2\cdot A=2^1+2^2+2^3+...+2^{2015}+2^{2016}\)

\(2A-A=2^1+2^2+2^3+...+2^{2015}+2^{2016}-\left(1+2^1+2^2+...+2^{2015}\right)\)

\(A=2^{2016}-1\)

giúp minh

$\dfrac24$
vì $\dfrac24=\dfrac{2 \times 1}{2 \times 2}=\dfrac12$

\(A=1+2^1+2^2+...+2^{2015}\)

\(\Rightarrow A=\dfrac{2^{2015+1}-1}{2-1}\)

\(\Rightarrow A=2^{2016}-1\)

\(\Rightarrow A+1=2^{2016}\)

\(\Rightarrow A+1=\left(2^3\right)^{672}\)

\(\Rightarrow A+1=8^{672}\)

Mình ra giống trí nha