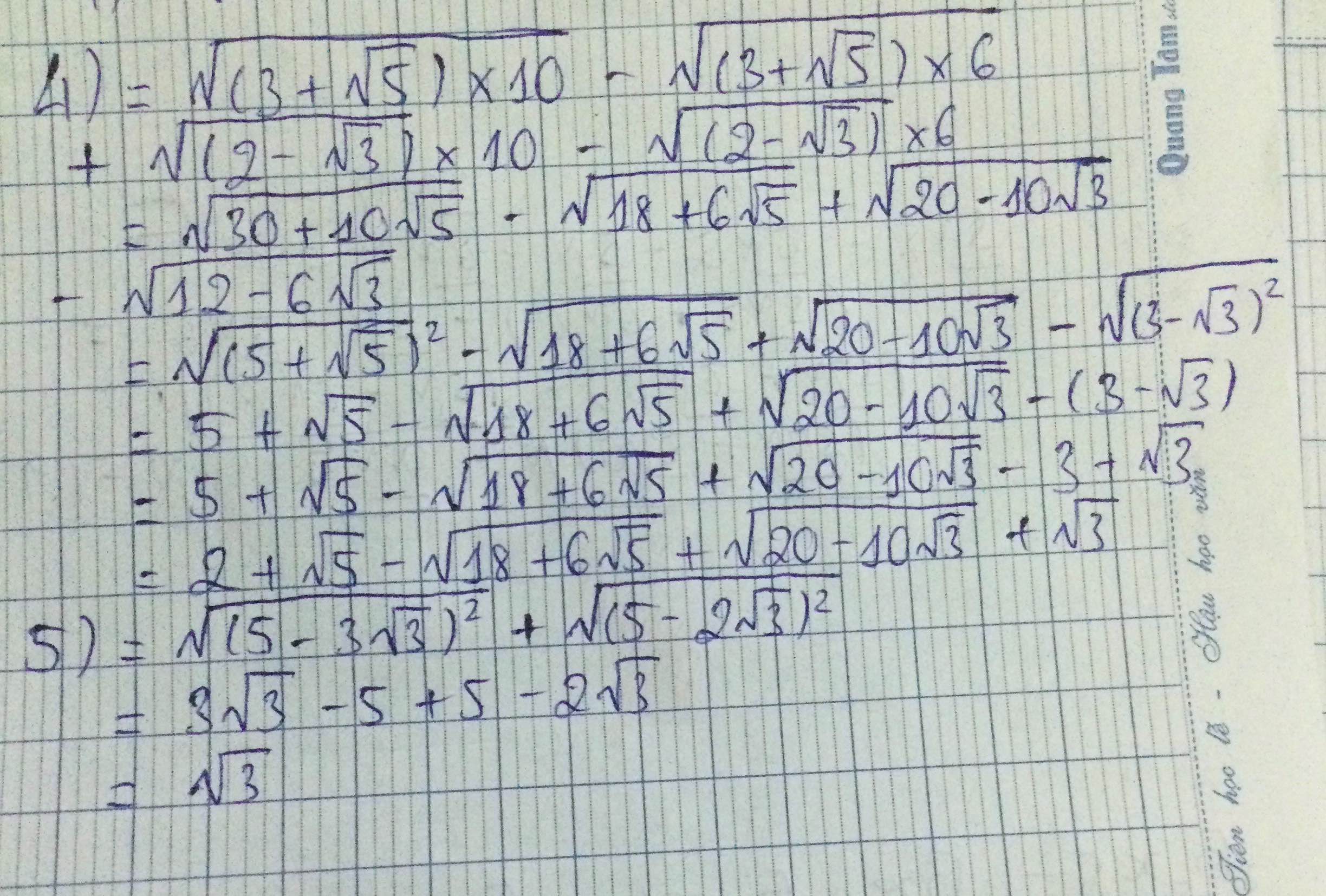Giải giúp em vs ạ
Em cảm ơn



Những câu hỏi liên quan

giải giúp em vs ạ. em cảm ơn nhiều ạ .
1: \(\sqrt{\dfrac{1}{200}}=\dfrac{\sqrt{2}}{20}\)
2: \(\dfrac{5}{1-\sqrt{6}}=-1-\sqrt{6}\)
3: \(\dfrac{1}{1-\sqrt{2}}-\dfrac{1}{1+\sqrt{2}}\)
\(=\dfrac{1+\sqrt{2}-1+\sqrt{2}}{-1}\)
\(=-2\sqrt{2}\)
Đúng 0
Bình luận (0)
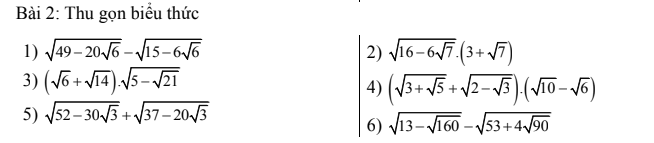
giải giúp em vs ạ em cảm ơn nhiều ạ.
2: Ta có: \(\sqrt{16-6\sqrt{7}}\cdot\left(3+\sqrt{7}\right)\)
\(=\left(3-\sqrt{7}\right)\left(3+\sqrt{7}\right)\)
=9-7
=2
3: Ta có: \(\left(\sqrt{6}+\sqrt{14}\right)\cdot\sqrt{5-2\sqrt{21}}\)
\(=\left(\sqrt{7}+\sqrt{3}\right)\left(\sqrt{7}-\sqrt{3}\right)\)
=7-3
=4
Đúng 2
Bình luận (0)
\(1,=\sqrt{\left(5+2\sqrt{6}\right)^2}-\sqrt{\left(3-\sqrt{6}\right)^2}=5+2\sqrt{6}-3+\sqrt{6}=2+3\sqrt{6}\\ 2,=\sqrt{\left(3-\sqrt{7}\right)^2}\left(3+\sqrt{7}\right)=\left(3-\sqrt{7}\right)\left(3+\sqrt{7}\right)=9-7=2\\ 3,=\left(\sqrt{3}+\sqrt{7}\right)\sqrt{10-2\sqrt{21}}=\left(\sqrt{3}+\sqrt{7}\right)\sqrt{\left(\sqrt{7}-\sqrt{3}\right)^2}\\ =\left(\sqrt{7}+\sqrt{3}\right)\left(\sqrt{7}-\sqrt{3}\right)=7-3=4\\ 4,=\left(\sqrt{5}-\sqrt{3}\right)\left(\sqrt{6+2\sqrt{5}}+\sqrt{4-2\sqrt{3}}\right)\\ =\left(\sqrt{5}-\sqrt{3}\right)\left(\sqrt{5}+1+\sqrt{3}-1\right)\\ =\left(\sqrt{5}-\sqrt{3}\right)\left(\sqrt{5}+\sqrt{3}\right)=5-3=2\)
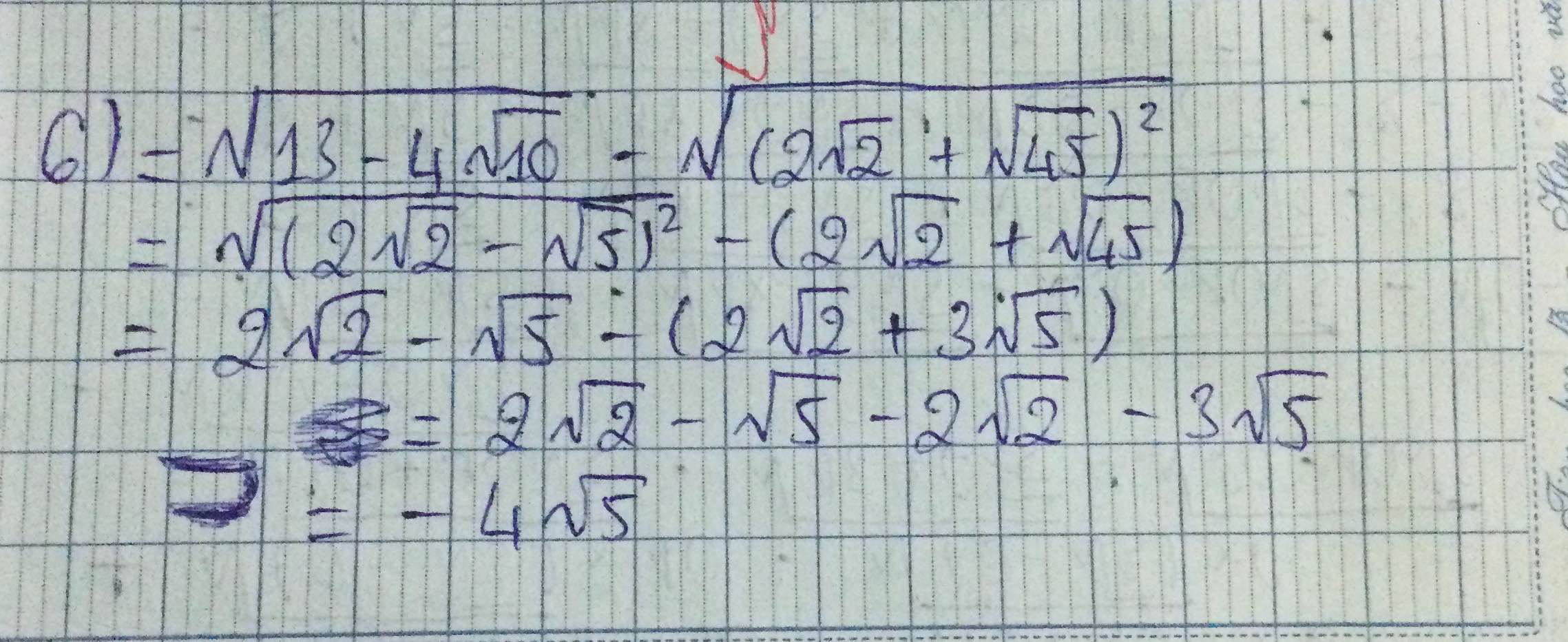
\(5,\\ =\sqrt{\left(3\sqrt{3}-5\right)^2}+\sqrt{\left(5-2\sqrt{3}\right)^2}=3\sqrt{3}-5+5-2\sqrt{3}=\sqrt{3}\\ 6,=\sqrt{13-4\sqrt{10}}-\sqrt{53+12\sqrt{10}}\\ =\sqrt{\left(2\sqrt{2}-\sqrt{5}\right)^2}-\sqrt{\left(3\sqrt{5}-2\sqrt{2}\right)^2}\\ =2\sqrt{2}-\sqrt{5}-3\sqrt{5}+2\sqrt{2}=4\sqrt{2}-4\sqrt{5}\)
Đúng 2
Bình luận (0)
Giúp em giải gấp vs ạ❤️Em cảm ơn trc ạ
1 D
2 C
3 D
4 C
5 B
6 D
7 A
8 A
9 B
10 D
11 C
12 B
Đúng 1
Bình luận (0)
 ai giải giùm em câu 6 vs ạ cho em lời giải chi tiết và vẽ hình giúp em vs ạ cảm ơn mn
ai giải giùm em câu 6 vs ạ cho em lời giải chi tiết và vẽ hình giúp em vs ạ cảm ơn mn
giúp em giải bài 5 vs ạ! Em cảm ơn
Khó thấy quá bạn ơi, bạn chụp lại đi
Đúng 0
Bình luận (1)
Giải giúp em bài 4,5 vs ạ . Em cảm ơn .
Bài 5:
\(a,\dfrac{2}{2x-4}=\dfrac{2}{2\left(x-2\right)}=\dfrac{1}{x-2};\dfrac{3}{3x-6}=\dfrac{3}{3\left(x-2\right)}=\dfrac{1}{x-2}\\ b,\dfrac{1}{x+4}=\dfrac{2\left(x-4\right)}{2\left(x+4\right)\left(x-4\right)};\dfrac{1}{2x+8}=\dfrac{x-4}{2\left(x+4\right)\left(x-4\right)}\\ \dfrac{3}{x-4}=\dfrac{6\left(x+4\right)}{2\left(x-4\right)\left(x+4\right)}\\ c,\dfrac{1}{x^2-1}=\dfrac{1}{\left(x-1\right)\left(x+1\right)};\dfrac{2}{x-1}=\dfrac{2\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}\\ \dfrac{2}{x+1}=\dfrac{2\left(x-1\right)}{\left(x-1\right)\left(x+1\right)}\\ d,\dfrac{1}{2x}=\dfrac{x-2}{2x\left(x-2\right)};\dfrac{2}{x-2}=\dfrac{4x}{2x\left(x-2\right)};\dfrac{3}{2x\left(x-2\right)}\text{ giữ nguyên}\)
Đúng 2
Bình luận (0)
Bài 4:
\(a,\dfrac{x^2-4x+4}{x^2-2x}=\dfrac{\left(x-2\right)^2}{x\left(x-2\right)}=\dfrac{x-2}{x}=\dfrac{\left(x-2\right)\left(x-1\right)}{x\left(x-1\right)}\\ \dfrac{x+1}{x^2-1}=\dfrac{1}{x-1}=\dfrac{x}{x\left(x-1\right)}\\ b,\dfrac{x^3-2^3}{x^2-4}=\dfrac{\left(x-2\right)\left(x^2+2x+4\right)}{\left(x-2\right)\left(x+2\right)}=\dfrac{x^2+2x+4}{x+2};\dfrac{3}{x+2}\text{ giữ nguyên}\)
Đúng 0
Bình luận (0)
Mn giúp em giải vs ạ em cảm ơn nhiều 

Giải giúp em vs ạ. Em xin cảm ơn o(︶︿︶)o
Bài 1:
a) Ta có: \(A=3\sqrt{49}-\sqrt{25}\)
\(=3\cdot7-5\)
=21-5=16
b) Ta có: \(B=\sqrt{\left(3-2\sqrt{5}\right)^2}-\sqrt{20}\)
\(=2\sqrt{5}-3-2\sqrt{5}\)
=-3
Đúng 0
Bình luận (0)
Bài 2:
a) Ta có: \(P=\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}+\dfrac{\sqrt{x}}{x-\sqrt{x}}\right):\dfrac{\sqrt{x}+1}{3}\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\cdot\dfrac{3}{\sqrt{x}+1}\)
\(=\dfrac{3}{\sqrt{x}+1}\)
b) Để P=1 thì \(\sqrt{x}+1=3\)
hay x=4(thỏa ĐK)
Đúng 0
Bình luận (0)
Mong mn giúp em giải pt này vs ạ! Em đg cần gấp lắm ạ ! Em cảm ơn
ĐKXĐ: \(x\ge1\)
\(\sqrt{x-1-4\sqrt{x-1}+4}+\sqrt{x-1-6\sqrt{x-1}+9}=0\)
\(\Leftrightarrow\sqrt{\left(\sqrt{x-1}-2\right)^2}+\sqrt{\left(3-\sqrt{x-1}\right)^2}=0\)
\(\Leftrightarrow\left|\sqrt{x-1}-2\right|+\left|3-\sqrt{x-1}\right|=0\)
Do \(\left|\sqrt{x-1}-2\right|+\left|3-\sqrt{x-1}\right|\ge\left|\sqrt{x-1}-2+3-\sqrt{x-1}\right|=1>0\) với mọi x thuộc TXĐ
\(\Rightarrow\) Phương trình đã cho vô nghiệm
Đúng 1
Bình luận (0)