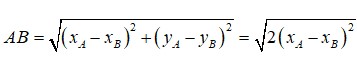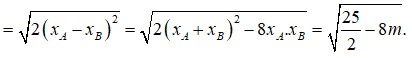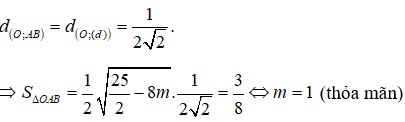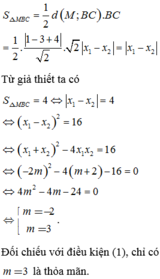tìm tất cả các giá trị của tham số m đẻ đường thẳng(d): y=-2x+4 cắt đồ thị hàm số y=x^2+2mx+1-3m tại A và B sao cho tam giác OAB có diện tích bằng \(12\sqrt{2}\)

Những câu hỏi liên quan
tìm tất cả các giá trị của tham số m đẻ đường thẳng(d): y=-2x+4 cắt đồ thị hàm số y=x^2+2mx+1-3m tại A và B sao cho tam giác OAB có diện tích bằng 12\(\sqrt{2}\)
Phương trình hoành độ giao điểm:
$x^2+2mx+1-3m=-2x+4\iff x^2+2x(m+1)-3-3m=0$.
$\Delta'=(m+1)^2+3+3m=(m+1)(m+4)$
Hai đồ thì cắt nhau tại hai điểm phân biệt $A,B$ khi và chỉ khi $\Delta'>0\iff (m+1)(m+4)>0(*)$.
Giả sử: $A(a;-2a+4);B(b;-2b+4),(AB)\equiv (d): y+2x-4=0$.
Theo $Viet$, ta có: $a+b=-2m-2;ab=-3-3m$.
Theo GT: $S_{OAB}=\frac{1}{2}.d(O,AB).AB(2)$.
Mà: $d(O;AB)=\frac{|-4|}{\sqrt{2^2+1^2}}=\frac{4}{\sqrt{5}}$.
$(2)\implies AB=\frac{2S_{OAB}}{d(O;AB)}=6\sqrt{10}$.
\iff AB^2=360\iff 5(a-b)^2=360\iff (a-b)^2=72\iff (a+b)^2-4ab=72$.
$\iff 4(m+1)^2+12(m+1)-72=0\iff m+1=3(n)...v...m+1=-6(n)(\text{ do (1) })$.
Vậy: $m=2...v...m=-7$ là hai giá trị cần tìm.
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m để đồ thị (C) của hàm số
y
2
x
+
3
x
-
1
cắt đường thẳng
△
:
y
x
+
m
tại hai điểm phân biệt A và B sao cho tam giác OAB vuông tại O A.
m
-
3
B. ...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để đồ thị (C) của hàm số y = 2 x + 3 x - 1 cắt đường thẳng △ : y = x + m tại hai điểm phân biệt A và B sao cho tam giác OAB vuông tại O
A. m = - 3
B. m = 6
C. m = 5
D. m = - 1
Tìm tất cả các giá trị của tham số m để đồ thị hàm số
y
2
x
x
−
2
cắt đường thẳng
y
x
+
m
tại hai điểm phân biệt A,B sao cho tam giác OAB nhận
G
1
;
5
3
làm trọng tâm. A. m3 B. m4 C...
Đọc tiếp
Tìm tất cả các giá trị của tham số m để đồ thị hàm số y = 2 x x − 2 cắt đường thẳng y = x + m tại hai điểm phân biệt A,B sao cho tam giác OAB nhận G 1 ; 5 3 làm trọng tâm.
A. m=3
B. m=4
C. m=1
D. m=7
Đáp án C
Điều kiện: x≠2.
Hoành độ giao điểm của hai đồ thị là nghiệm của phương trình
2 x x − 2 = x + m ⇔ 2 x x − 2 − x − m = 0 ⇔ 2 x − x 2 + 2 x − m x + 2 m x − 4 = 0 ⇔ − x 2 + 4 − m x + 2 m x − 2 = 0.
Để hai đồ thị hàm số giao nhau tại hai điểm phân biệt A,B ta có
4 − m 2 + 8 m > 0 g 2 ≠ 0 ⇔ m 2 + 16 > 0 − 4 + 8 − 2 m + 2 m ≠ 0
thỏa mãn với mọi m ∈ ℝ .
Theo bài ra ta có x A + x B + x O = 3 x A + m + x B + m + y O = 7 ⇔ 4 − m = 3 4 − m + 2 m = 5 ⇔ m = 1 .
Vậy m=1 thỏa mãn điều kiện đề bài.
Đúng 0
Bình luận (0)
Tìm các giá trị thực của tham số m để đường thẳng d: y= 2x +2y -1=0 cắt đồ thị (Cm): Y=( -x+m)/(x+2) tại hai điểm phân biệt A, B sao cho tam giác OAB có diện tích bằng 1 (O là gốc tọa độ)
hoành độ giao điểm là nghiệm của pt
\(\frac{-x+m}{x+2}=\frac{1-2x}{2}\) với x khác -2
\(\frac{-x+m}{x+2}=\frac{1-2x}{2}\Leftrightarrow\frac{-2x+2m}{2\left(x+2\right)}=\frac{\left(1-2x\right)\left(x+2\right)}{2\left(x+2\right)}\Leftrightarrow-2x+2m=\left(1-2x\right)\left(x+2\right)\Leftrightarrow-2x+2m=x-2x^2+2-4x\Leftrightarrow2x^2+x+2m-2=0\)
để đt d cắt đồ thị hàm số tại 2 điểm pt thì pt trên có 2 nghiệm phân biệt khác -2
làm tương tự như câu dưới......
Đúng 0
Bình luận (1)
Cho hàm số \(y=\frac{2x-1}{x+1}\) có đồ thị (C). Tìm tất cả các giá trị của tham số m để đường thẳng \(y=mx+2\) cắt (C) tại hai điểm phân biệt A, B sao cho tam giác OAB vuông tại O
Hoành độ giao điểm của d : y = mx+2 với (C) là nghiệm phương trình :
\(\begin{cases}x>0\\\log^2_2x-\log_2x^2-3\ge0\end{cases}\)
Dễ thấy với m = 0 thì (1) vô nghiệm. Đường thẳng d cắt (C) tại hai điểm phân biệt khi và chỉ khi (1) có 2 nghiệm phân biệt khác -1. Điều kiện là
\(\begin{cases}\Delta>0\\m\left(-1\right)^2+m\left(-1\right)+3\ne0\end{cases}\) \(\Leftrightarrow m^2-12m>0\) \(\Leftrightarrow m<0\) hoặc m > 12 (*)
Với (*) giả sử x1, x2 là 2 nghiệm phân biệt của (1), khi đó tọa độ các giao điểm là :
\(A\left(x_1;mx_1+2\right);B\left(x_2;mx_2+2\right)\)
Dễ thất điểm O không thuộc d nên ABO là một tam giác.
Tam giác ABO vuông tại O khi và chỉ khi :
\(\overrightarrow{OA}.\overrightarrow{OB}=0\Leftrightarrow\left(1+m^2\right)x_1x_2+2m\left(x_1+x_2\right)+4=0\)
Áp dụng định lí Viet ta có : \(x_1+x_2=-1;x_1x_2=\frac{3}{m}\)
Thay vào trên ta được :
\(m^2+4m+3=0\Leftrightarrow m=-3\) hoặc \(m=-1\) (thỏa mãn (*)
Vậy \(m=-3\) hoặc \(m=-1\)
Đúng 0
Bình luận (0)
Cho hàm số
y
m
-
3
x
x
+
2
Giá trị m để đường thẳng d: 2x+2y-10 cắt đồ thị hàm số tại hai điểm A, B sao cho diện tích tam giác OAB bằng 3/8 là A. 1 B. 2 C. 1/2 D. -1
Đọc tiếp
Cho hàm số y = m - 3 x x + 2 Giá trị m để đường thẳng d: 2x+2y-1=0 cắt đồ thị hàm số tại hai điểm A, B sao cho diện tích tam giác OAB bằng 3/8 là
A. 1
B. 2
C. 1/2
D. -1
cho hàm số y = x2 -2mx -m -2 (1) ( m là tham số thực )
tìm tất cả các giá trị của tham số m để đồ thị hàm số (1) cắt đường thẳng d: y = 2x -7 tại 2 điểm phân biệt có hoành độ đều lớn hơn -1
Tìm tất cả các giá trị của m để đường thẳng d: yx+4 cắt đồ thị hàm số
y
x
3
+
2
m
x
2
+
m
+
3
x
+
4
tại 3 điểm phân biệt A(0;4), B và C sao cho diện tích tam giác MBC bằng 4, với M(1;3) A.
m...
Đọc tiếp
Tìm tất cả các giá trị của m để đường thẳng d: y=x+4 cắt đồ thị hàm số y = x 3 + 2 m x 2 + m + 3 x + 4 tại 3 điểm phân biệt A(0;4), B và C sao cho diện tích tam giác MBC bằng 4, với M(1;3)
A. m = 2 m = 3
B. m = - 2 m = 3
C. m = 3
D. m = − 3 m = − 2
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y= x3-3mx2+ 3m3 có hai điểm cực trị A và B sao cho tam giác OAB có diện tích bằng 48.
A. m= 1.
B . m = 2
C. m= -2
D. Đáp án khác
+ Đạo hàm y’ = 3x2- 6mx= 3x( x- 2m)
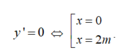
Đồ thị hàm số có hai điểm cực trị khi và chỉ khi :m≠0. (1)
+ Tọa độ các điểm cực trị của đồ thị hàm số là A( 0 ; 3m3) ; B( 2m; -m3)
Ta có: O A → ( 0 ; 3 m 3 ) ⇒ O A = 3 m 3 ( 2 )
Ta thấy A ∈ O y ⇒ O A ≡ O y ⇒ d ( B ; O A ) = d ( B ; O y ) = 2 m (3)
+ Từ (2) và (3) suy ra S= ½. OA.d(B ; OA)=3m4.
Do đó: S ∆ O A B = 48 ⇔ 3 m 4 = 48 ⇔ m = ± 2 (thỏa mãn (1) ).
Chọn D.
Đúng 0
Bình luận (0)