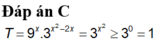a) \(N=-1-x-x^2=-\left(x^2+x+\dfrac{1}{4}\right)-\dfrac{3}{4}=-\left(x+\dfrac{1}{2}\right)^2-\dfrac{3}{4}\le-\dfrac{3}{4}\)

\(maxN=-\dfrac{3}{4}\Leftrightarrow x=-\dfrac{1}{2}\)

b) \(B=3x^2+4x-13=3\left(x^2+\dfrac{4}{3}x+\dfrac{4}{9}\right)-\dfrac{35}{3}=3\left(x+\dfrac{2}{3}\right)^2-\dfrac{35}{3}\ge-\dfrac{35}{3}\)

\(minB=-\dfrac{35}{3}\Leftrightarrow x=-\dfrac{2}{3}\)

a: Ta có: \(N=-x^2-x-1\)

\(=-\left(x^2+x+1\right)\)

\(=-\left(x^2+2\cdot x\cdot\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{3}{4}\right)\)

\(=-\left(x+\dfrac{1}{2}\right)^2-\dfrac{3}{4}\le-\dfrac{3}{4}\forall x\)

Dấu '=' xảy ra khi \(x=-\dfrac{1}{2}\)

b: ta có: \(B=3x^2+4x-13\)

\(=3\left(x^2+\dfrac{4}{3}x-\dfrac{13}{3}\right)\)

\(=3\left(x^2+2\cdot x\cdot\dfrac{2}{3}+\dfrac{4}{9}-\dfrac{43}{9}\right)\)

\(=3\left(x+\dfrac{2}{3}\right)^2-\dfrac{43}{3}\ge-\dfrac{43}{3}\forall x\)

Dấu '=' xảy ra khi \(x=-\dfrac{2}{3}\)

f (x) = 3x² + 2x³ - 6x - 2

bậc của đa thức là: 3

g(x) = 5x² + 9 - 2x³ - 3x² - 4x + 2x³ - 2

g(x) = ( 5x² - 3x² ) + ( 9 -2) + ( - 2x³ + 2x³ ) - 4x

g(x) = 2x² + 7 - 4x

bậc của đa thức là : 2

Đáp án D

a.

\(A=\dfrac{2013}{x^2}-\dfrac{2}{x}+1=2013\left(\dfrac{1}{x}-\dfrac{1}{2013}\right)^2+\dfrac{2012}{2013}\ge\dfrac{2012}{2013}\)

Dấu "=" xảy ra khi \(x=2013\)

b.

\(B=\dfrac{4x^2+2-4x^2+4x-1}{4x^2+2}=1-\dfrac{\left(2x-1\right)^2}{4x^2+2}\le1\)

\(B_{max}=1\) khi \(x=\dfrac{1}{2}\)

\(B=\dfrac{-2x^2-1+2x^2+4x+2}{4x^2+2}=-\dfrac{1}{2}+\dfrac{\left(x+1\right)^2}{2x^2+1}\ge-\dfrac{1}{2}\)

\(B_{max}=-\dfrac{1}{2}\) khi \(x=-1\)

- Ta có:

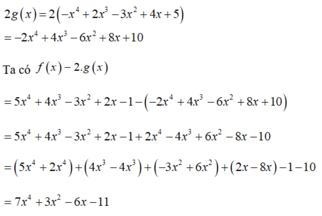
Hệ số cần tìm là -11

Chọn đáp án C

+) Ta có

2 g ( x ) = 2 − x 4 + 2 x 3 − 3 x 2 + 4 x + 5 = − 2 x 4 + 4 x 3 − 6 x 2 + 8 x + 10  Ta có  f ( x ) − 2 ⋅ g ( x ) = 5 x 4 + 4 x 3 − 3 x 2 + 2 x − 1 − − 2 x 4 + 4 x 3 − 6 x 2 + 8 x + 10 = 5 x 4 + 4 x 3 − 3 x 2 + 2 x − 1 + 2 x 4 − 4 x 3 + 6 x 2 − 8 x − 10 = 5 x 4 + 2 x 4 + 4 x 3 − 4 x 3 + − 3 x 2 + 6 x 2 + ( 2 x − 8 x ) − 1 − 1 = 7 x 4 + 3 x 2 − 6 x − 11

Hệ số cần tìm là -11

Chọn đáp án C

\(A=x^2+2x+5=\left(x^2+2x+1\right)+4=\left(x+1\right)^2+4\ge4\)

Kl: Min_A = 4

\(B=x^2-x+1=\left(x^2-2\cdot\dfrac{1}{2}x+\dfrac{1}{4}\right)+\dfrac{3}{4}=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\)

kl:.......

\(C=5x^2+5x+1=5\left(x^2+2\cdot\dfrac{1}{2}x+\dfrac{1}{4}\right)+1-\dfrac{5}{4}=5\left(x+\dfrac{1}{2}\right)^2-\dfrac{1}{4}\ge-\dfrac{1}{4}\)

kl:.......

\(D=3x^2+4x+2=3\left(x^2+2\cdot\dfrac{2}{3}x+\dfrac{4}{9}\right)+2-\dfrac{4}{3}=3\left(x+\dfrac{2}{3}\right)^2+\dfrac{2}{3}\ge\dfrac{2}{3}\)

kl:......

\(E=\dfrac{1}{2}\cdot x^2+x-1=\dfrac{1}{2}\left(x^2+2x+1\right)-1-\dfrac{1}{2}=\dfrac{1}{2}\left(x+1\right)^2+\dfrac{3}{2}\ge\dfrac{3}{2}\)

kl:............

\(F=\dfrac{1}{9}x^2+3x+2=\dfrac{1}{3}\left(x^2+2\cdot\dfrac{1}{2}x+\dfrac{1}{4}\right)+2-\dfrac{1}{12}=\dfrac{1}{3}\left(x+\dfrac{1}{2}\right)^2+\dfrac{23}{12}\ge\dfrac{23}{12}\)

kl:..........