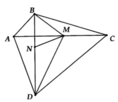
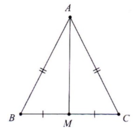
Cho ∆ABC, gọi M là trung điểm của BC. Chứng minh AM>AB+AC/2

Những câu hỏi liên quan
Cho tam giác ABC, gọi M là trung điểm của BC. Chứng minh rằng \(\dfrac{AB+AC-BC}{2}\) < AM < \(\dfrac{AB+AC}{2}\)
Cho tam giác ABC. Gọi M là trung điểm của BC
a) Chứng minh AM < \(\dfrac{AB+AC}{2}\)
b) Cho bốn điểm A, B, C, D như hình vẽ. gọi thứ tự là trung điểm của AC và BD. Chứng minh AB+BC+CD+DA > 4.MN
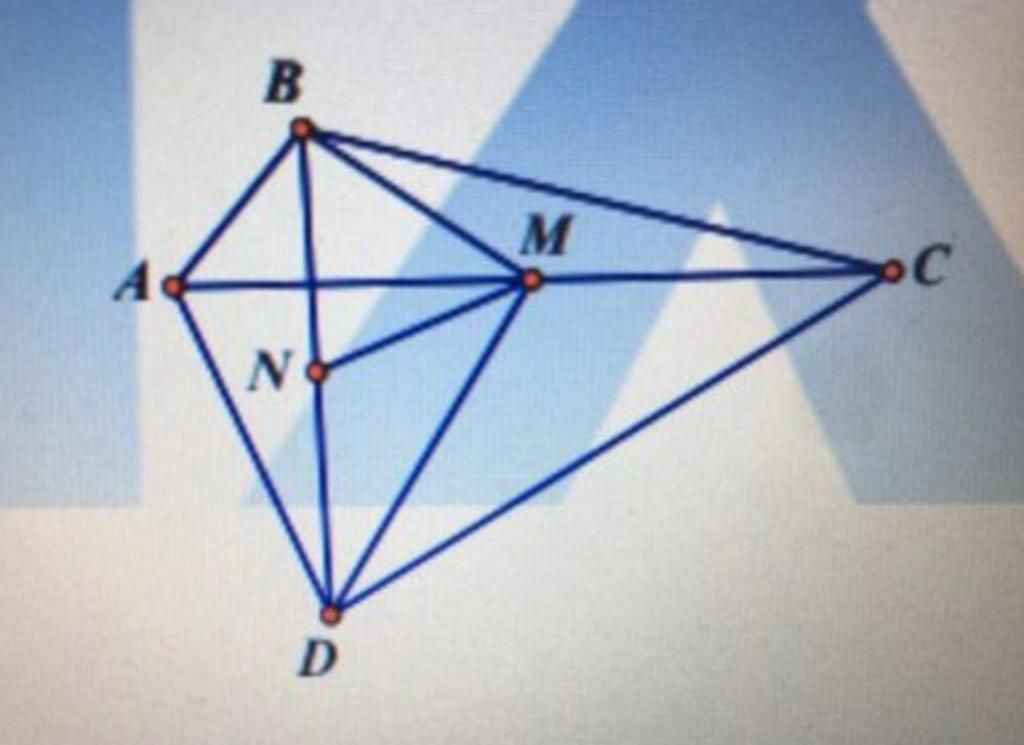
a:
Lấy D sao cho M là trung điểm của AD
Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
=>ABDC là hình bình hành
(AB+AC)=AB+BD>AD
=>AB+AC>2AM
=>(AB+AC)/2>AM
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A(AB AC) có M là trung điểm của BC. Trên tia AM lấy điểm D sao cho AM MD. a) Chứng minh ΔAMCΔDMB . b) Chứng minh BD // AC và AD BC. c) Gọi K là trung điểm của AC. Chứng minh MK⊥BD.
Đọc tiếp
Cho tam giác ABC vuông tại A(AB < AC) có M là trung điểm của BC. Trên tia AM lấy điểm D sao cho AM = MD.
a) Chứng minh ΔAMC=ΔDMB .
b) Chứng minh BD // AC và AD = BC.
c) Gọi K là trung điểm của AC. Chứng minh MK⊥BD.
a) Xét tam giác AMC và tam giác DMB có:
AM=MD(gt)
\(\widehat{BMD}=\widehat{AMC}\left(đối.đỉnh\right)\)
BM=MC(M là trung điểm BC)
=> ΔAMC=ΔDMB(c.g.c)
b) Ta có: \(\widehat{DBM}=\widehat{MCA}\left(\Delta AMC=\Delta DMB\right)\)
Mà 2 góc này so le trong
=> BD//AC
Xét tứ giác ABDC có:
M là trung điểm chung của AD,BC
=> ABDC là hình bình hành
Mà \(\widehat{BAC}=90^0\)
=> ABDC là hình chữ nhật
=> AD=BC
c) Xét tam giác AMK và tam giác CMK có:
MK chung
AK=KC
\(AM=MC\left(=\dfrac{1}{2}AD=\dfrac{1}{2}BC\right)\)
=> ΔAMK=ΔCMK(c.c.c)
=> \(\widehat{MKA}=\widehat{MKC}=180^0:2=90^0\Rightarrow MK\perp AC\)
Mà AC//BD(ABDC là hình chữ nhật)
\(\Rightarrow MK\perp BD\)
Đúng 1
Bình luận (2)
a) Xét tam giác AMC và tam giác DMB có:
AM=MD(gt)
ˆBMD=ˆAMC(đối.đỉnh)BMD^=AMC^(đối.đỉnh)
BM=MC(M là trung điểm BC)
=> ΔAMC=ΔDMB(c.g.c)
b) Ta có: ˆDBM=ˆMCA(ΔAMC=ΔDMB)DBM^=MCA^(ΔAMC=ΔDMB)
Mà 2 góc này so le trong
=> BD//AC
Xét tứ giác ABDC có:
M là trung điểm chung của AD,BC
=> ABDC là hình bình hành
Mà ˆBAC=900BAC^=900
=> ABDC là hình chữ nhật
=> AD=BC
c) Xét tam giác AMK và tam giác CMK có:
MK chung
AK=KC
Đúng 0
Bình luận (0)
a) Xét tam giác AMC và tam giác DMB có:
AM=MD(gt)
ˆBMD=ˆAMC(đối.đỉnh)BMD^=AMC^(đối.đỉnh)
BM=MC(M là trung điểm BC)
=> ΔAMC=ΔDMB(c.g.c)
b) Ta có: ˆDBM=ˆMCA(ΔAMC=ΔDMB)DBM^=MCA^(ΔAMC=ΔDMB)
Mà 2 góc này so le trong
=> BD//AC
Xét tứ giác ABDC có:
M là trung điểm chung của AD,BC
=> ABDC là hình bình hành
Mà ˆBAC=900BAC^=900
=> ABDC là hình chữ nhật
=> AD=BC
c) Xét tam giác AMK và tam giác CMK có:
MK chung
AK=KC
Đúng 0
Bình luận (0)
Cho tam giác ABC. Gọi M là trung điểm của BC.
a) Chứng minh A M < A B + A C 2
b) Cho bốn điểm A, B, C, D như hình vẽ. Gọi thứ tự là trung điểm của AC và BD. Chứng minh AB + BC + C + DA > 4MN
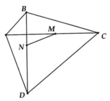
Bài 5 Cho ABC nhọn (AB<AC). Gọi D là trung điểm của AC. Trên tia đối của tia DB
lấy điểm M sao cho DB = DM.
a) Chứng minh AM = BC và AM // BC.
b) Gọi E là trung điểm AB. Trên tia đối của tia EC lấy điểm N sao cho EN = EC. Chứng
minh AN // BC và AN = BC.
c) Chứng minh M, A, N thẳng hàng và A là trung điểm của MN.
a: Xét tứ giác ABCM có
D là trung điểm của AC
D là trung điểm của BM
Do đó: ABCM là hình bình hành
Suy ra: AM//BC và AM=BC
Đúng 0
Bình luận (0)
bài 4 : trên tia đối của tia AB và tia AC của ABC lấy AB'=AB, AC'=AC . chứng minh
a) BC=BC'
b) gọi M là trung điểm của BC , M' là trung điểm của B'C' . Chứng minh ba điểm M , A, M' thẳng hàng
c) AM=AM'
Cho ABC có AB AC = , lấy M là trung điểm của BC . a) Chứng minh: = ABM ACM b) Chứng minh: AM BC ⊥ c) Lấy điểm E thuộc cạnh AB , lấy điểm F thuộc cạnh AC sao cho AE AF = . Gọi I là giao điểm của EF và AM . Chứng minh: = AIE AIF và EF BC // .
a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó: ΔABM=ΔACM
b: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
c: Xét ΔABC có
AE/AB=AF/AC
Do đó: EF//BC
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB = AC. Gọi M là trung điểm của cạnh BC. Chứng minh:
a) AM là phân giác của B A C ^
b) A M ⊥ B C .
Cho tam giác ABC có A=40° , AB=AC. Gọi M là trung điểm của BC.
a/ chứng minh ABM=ACM
b/ lấy D∈ AB, E∈ AC sao cho AD=AE. Chứng minh DE⊥AM; BC⊥AM
a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó: ΔABM=ΔACM
b: Ta có: DB+AD=AB
EC+AE=AC
mà AD=AE
và AB=AC
nên DB=EC
Xét ΔDBM và ΔECM có
DB=EC
\(\widehat{B}=\widehat{C}\)
MB=MC
Do đó: ΔDBM=ΔECM
Suy ra: MD=ME
Ta có: AD=AE
nên A nằm trên đường trung trực của DE(1)
ta có: MD=ME
nên M nằm trên đường trung trực của DE(2)
Ta có: AB=AC
nên A nằm trên đường trung trực của BC(3)
Ta có: MB=MC
nên M nằm trên đường trung trực của BC(4)
Từ (1) và (2) suy ra AM là đường trung trực của DE
hay AM\(\perp\)DE
Từ (3) và (4) suy ra AM là đường trung trực của BC
hay AM\(\perp\)BC
Đúng 0
Bình luận (0)