Các câu hỏi tương tự
Cho tam giác ABC. Trên tia đối của tia AB và AC lân lượt lấy các điểm C’ và B’ sao cho AB = AB’ và AC = AC’. Gọi M, M’ tương ứng là trung điểm của BC và B’C’. Chứng minh:
a/ BC = B’C’ b/ BC//B’C’ c) AM = AM’ d*/ A, M, M’ thẳng hàng
cho tam giác ABC có AB=AC và BC<AB,gọi M là trung điểm của BC
a)c/m: tam giác ABM=tam giác ACM và AM là tia phân giác của góc BAC
b)trên cạnh AB lấy điểm D sao cho CB=CD.Kẻ tia phân giác của góc BCD,tia này cắt cạnh BD tại N . CHỨNG MINH: CN vuông góc BD
c)trên tia đối của tia CA lấy điểm E sao cho AD=CE, chứng minh: BE-CE=2BN
cho tam giác abc có AB=AC,gọi AM là tia phân giác của góc A(M thuộc BC)
a Chứng minh tam giác AMB = tam giác AMC
b Chứng minh M là trung điểm của cạnh BC và AM ⊥ BC
c Trên tia AM lấy điểm K sao cho MA = MK. Chứng minh AB = CK và AB // CK
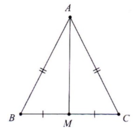
Cho tam giác ABC có AB = AC. Gọi M là trung điểm của BC. Chứng minh: a. ΔABM = ΔACM b. AM là tia phân giác của góc BAC c. AM là đường trung trực của đoạn thẳng BC
•Cho ta giác ABC có ABAC; m là trung điểm của BC Cho Δ ABC có AB AC. Gọi M là trung điểm của cạnh BC. •a, AM là phân giác của BAC và AM ⊥ BC •b,Qua C kẻ đường thẳng song song với AB cắt ACM tại D. CM: M là trung điểm của AD •c, Qua B kẻ đường thẳng vuông góc AC tại H. Tính số đo góc HBD
Đọc tiếp
•Cho ta giác ABC có AB=AC; m là trung điểm của BC Cho Δ ABC có AB = AC. Gọi M là trung điểm của cạnh BC. •a, AM là phân giác của BAC và AM ⊥ BC •b,Qua C kẻ đường thẳng song song với AB cắt ACM tại D. CM: M là trung điểm của AD •c, Qua B kẻ đường thẳng vuông góc AC tại H. Tính số đo góc HBD
cho tam giác ABC có AB=AC. Gọi M là trung điểm của BC. Chứng minh rằng: a) tam giác AMB= tam giác AMC b) AM là tia phân giác của BAC c) AM vuông góc với BC d) Vẽ At là tia phân giác của góc ngoài ở đỉnh A của tam giác ABC . Chứng minh : At // BC
Cho tam giác ABC có AB=AC . Gọi M là trung điểm của BC . Chứng minh:
a) góc B = góc C
b) AM là phân giác của góc BAC
c) AM là đường trung trực của BC
Cho tam giác ABC có AB=AC gọi M là trung điểm của cạnh BC
a) chứng minh 2 tam giác ABM và ACM bằng nhau
b chứng minh vuông góc vs BC
c AM là phân giác góc A
Cho tam giác ABC có AB = AC. Gọi M là một điểm nằm trong tam giác sao cho MB = MC. N là trung điểm của cạnh BC. Chứng minh rằng:
a) AM là tia phân giác của góc BAC^.
b) Ba điểm A, M, N thẳng hàng.
c) MN là đường trung trực của đoạn thẳng BC.