Giải nhanh giúp e với e đang cần gấp ạ

Những câu hỏi liên quan
Giải giúp e bài hình này với ạ
E đang cần gấp ạ , e cảm ơn

a: Xét ΔHAC vuông tại H và ΔABC vuông tại A có
\(\widehat{C}\) chung
Do đó: ΔHAC~ΔABC
b: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=15^2+20^2=625\)
=>BC=25
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}BH\cdot BC=BA^2\\AH\cdot BC=AB\cdot AC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH\cdot25=15^2=225\\AH\cdot25=15\cdot20=300\end{matrix}\right.\)
=>BH=9; AH=12
Đúng 0
Bình luận (0)
Mn giải giúp e bài này với ạ. E đang cần gấp
E đang cần gấp mn giải giúp e với đc k ạ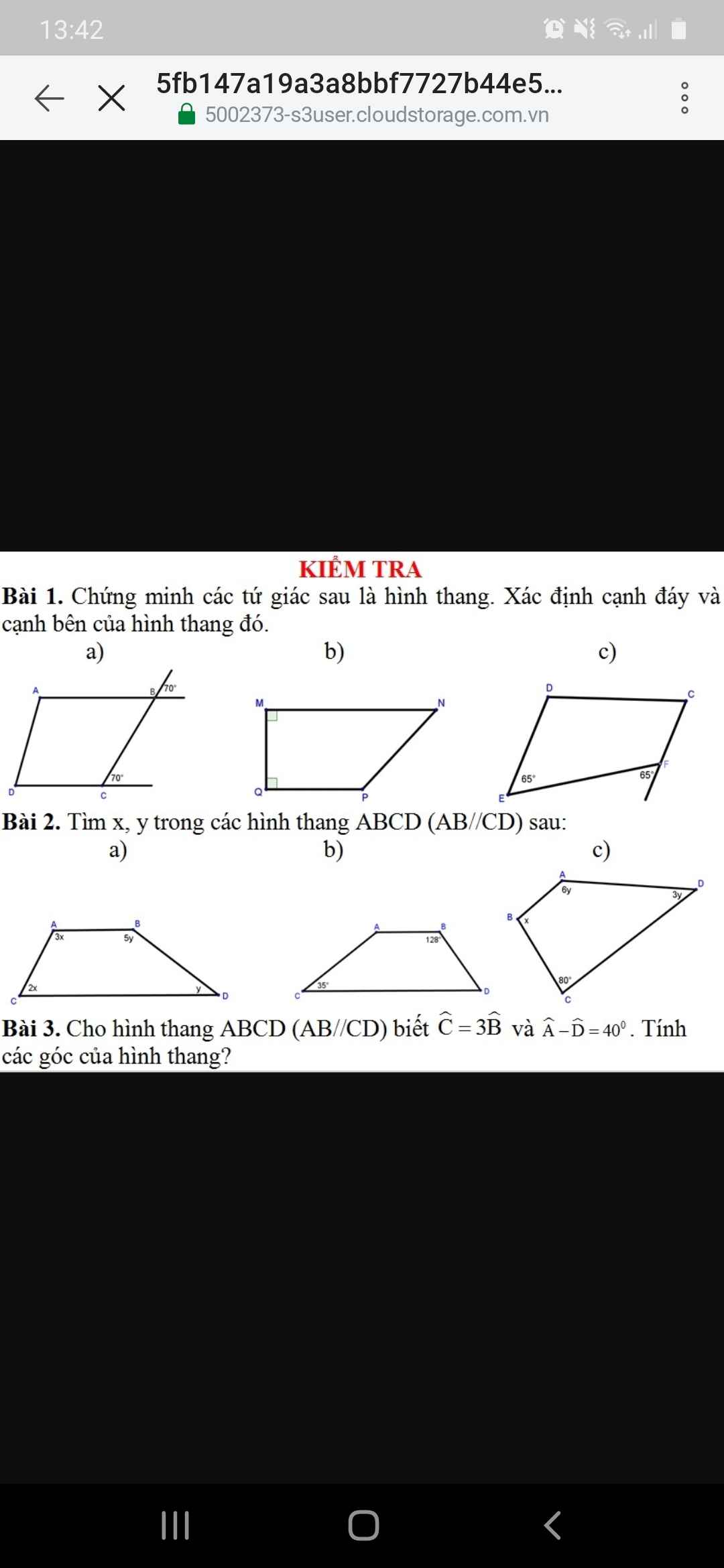
Bài 1
a) góc B=góc C=70 độ(gt)
=>AB//DC(đồng vị)
=> ABCD là hình thang
b)góc M+ góc Q=90 độ +90 độ=180 độ
=>MN//QP( hai góc trong cùng phía bù nhau)
=>MNPQ là hình thang
c)góc E= góc F=65 độ
=>DE//CF( slt)
=> DCFE là hình thang
Đúng 1
Bình luận (0)
Tham Khaor
Bài 1
a) góc B=góc C=70 độ(gt)
=>AB//DC(đồng vị)
=> ABCD là hình thang
b)góc M+ góc Q=90 độ +90 độ=180 độ
=>MN//QP( hai góc trong cùng phía bù nhau)
=>MNPQ là hình thang
c)góc E= góc F=65 độ
=>DE//CF( slt)
=> DCFE là hình thang
Đúng 1
Bình luận (0)
Bài 1:
a/ Góc B (ngoài) và góc C (ngoài) ở vị trí đồng vị, Góc B = Góc C ⇒ AB // CD
Vậy: ABCD là hình thang (đpcm), có cạnh đáy AB, CD và cạnh bên BC, AD
-----------
b/ MN ⊥ MQ, PQ ⊥ MQ ⇒ MN // PQ
Vậy: MNPQ là hình thang (đpcm), có cạnh đáy MN, PQ và cạnh bên NP, MQ
----------
c/ Góc DEF = Góc F (ngoài), hai góc ở vị trí so le trong ⇒ DE // CF
Vậy: CDEF là hình thang (đpcm), cạnh đáy DE, CF và cạnh bên CD, EF
==========
Bài 2:
a/ Ta có hai phương trình:
\(3x+2x=180\text{°}\) và \(y+5y=180\text{°}\) (do AB // CD)
Giải hai phương trình trên ta được: x=36° , y=30°
Vậy: \(\begin{matrix}\hat{A}=36\text{°}.3=108\text{°}\\\hat{B}=30\text{°}.5=150\text{°}\\\hat{C}=36\text{°}.2=72\text{°}\\\hat{D}=30\text{°}\end{matrix}\)
----------
b/ Do AB // CD, góc B = 128° và góc C = 35°
Vậy: \(\begin{matrix}\hat{A}=180\text{°}-35\text{°}=145\text{°}\\\hat{B}=128\text{°}\\\hat{C}=\hat{35\text{°}}\\\hat{D}=180\text{°}-128\text{°}=52\text{°}\end{matrix}\)
----------
c/ Do AB // CD
\(\Rightarrow x=180\text{°}-80\text{°}=100\text{°}\)
Ta có phương trình sau:
\(6y+3y=180\text{°}\)
Giải phương trình trên ta được y=20°
Vậy: \(\begin{matrix}\hat{A}=20\text{°}.6=120\text{°}\\\hat{B}=100\text{°}\\\hat{C}=80\text{°}\\\hat{D}=20\text{°}.3=60\text{°}\end{matrix}\)
==========
Bài 3:
- Do \(\hat{A}-\hat{D}=40\text{°}\Rightarrow\hat{A}=40\text{°}+\hat{D}\)
Ta có: \(\hat{A}+\hat{D}=180\text{°}\Leftrightarrow40\text{°}+2\hat{D}=180\text{°}\Leftrightarrow\hat{D}=70\text{°}\)
⇒ \(\hat{A}=110\text{°}\)
Mặt khác: \(\hat{A}+\hat{B}+\hat{C}+\hat{D}=360\text{°}\)
\(\Leftrightarrow110\text{°}+4\hat{B}+\hat{70\text{°}}=360\text{°}\)
\(\Leftrightarrow\hat{B}=45\text{°};\hat{C}=135\text{°}\)
Vậy: \(\begin{matrix}\hat{A}=110\text{°}\\\hat{B}=45\text{°}\\\hat{C}=135\text{°}\\\hat{D}=70\text{°}\end{matrix}\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời

 giải giúp e với ạ đang cần gấp!!
giải giúp e với ạ đang cần gấp!!
Ai giải được bài nào thì giải giúp e với ạ. em đang cần gấp ạ :((
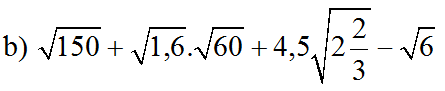
giải kỹ chi tiết từng bước giúp e với ạ!!!
e đang cần gấp lắm <3
b) Ta có: \(\sqrt{150}-\sqrt{1.6}\cdot\sqrt{60}+4.5\cdot\sqrt{2\dfrac{2}{3}}-\sqrt{6}\)
\(=5\sqrt{6}-4\sqrt{6}-\sqrt{6}+\dfrac{9}{2}\cdot\sqrt{\dfrac{8}{3}}\)
\(=\dfrac{9}{2}\cdot\dfrac{2\sqrt{2}}{\sqrt{3}}\)
\(=3\sqrt{6}\)
Đúng 1
Bình luận (1)
\(\sqrt{150}+\sqrt{1,6}.\sqrt{60}+4.5\sqrt{2\dfrac{2}{3}}-\sqrt{6}\\ =5\sqrt{6}+4\sqrt{6}+3\sqrt{6}-\sqrt{6}\\ =11\sqrt{6}\)
Đúng 0
Bình luận (0)
Tìm x, biết: x2 - 30 = 34
Giải nhanh giúp e với ạ, e cần rất gấp
\(x^2-30=34\)
\(x^2=34+30\)
\(x^2=64=8^2=\left(-8\right)^2\)
Vậy \(x=8^2\) hoặc \(x=\left(-8\right)^2\)
Đúng 1
Bình luận (0)
 Giải giúp e vs ạ ,e đang cần gấp
Giải giúp e vs ạ ,e đang cần gấp
giải chi tiết câu 16 đầu tiên cách làm và đáp án giúp e với ạ e đang cần gấp
Ta có : \(f\left(2\right)=2a+b-6\)
\(\lim\limits_{x\rightarrow2^+}\dfrac{x-\sqrt{x+2}}{x^2-4}=\lim\limits_{x\rightarrow2^+}\dfrac{x^2-x-2}{\left(x-2\right)\left(x+2\right)\left(x+\sqrt{x+2}\right)}\)
\(=\lim\limits_{x\rightarrow2^+}\dfrac{x+1}{\left(x+2\right)\left(x+\sqrt{x+2}\right)}=\dfrac{3}{16}\)
\(\lim\limits_{x\rightarrow2^-}x^2+ax+3b=4+2a+3b\)
H/s liên tục tại điểm x = 2 \(\Leftrightarrow\dfrac{3}{16}=2a+3b+4=2a+b-6\)
Suy ra : \(a=\dfrac{179}{32};b=-5\) => t = a + b = 19/32 . Chọn C
Đúng 1
Bình luận (0)


























