Vẽ giùm e cái hình ạ
Những câu hỏi liên quan
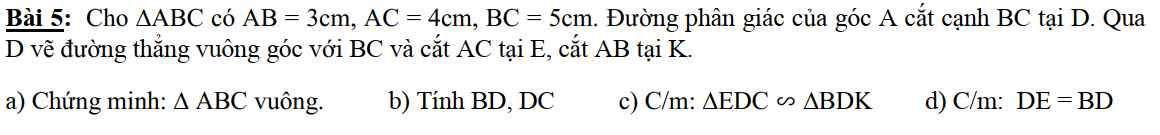
Cho góc xOy nhọn . Lấy điểm A trên tia Ox; điểm B trên tia Oy sao cho
OA=OB. Vẽ hai cung tròn tâm A và tâm B có cùng bán kính R ( R<OA). Hai cung này cắt nhau tại C và D
các bậc cao nhân vẽ giùm e cái hình vs ạ
Vẽ dùm e cái hình luôn với ạ đang cần gấp😅
a)
Δ\(ABD\) có \(AM\) là tia phân giác của \(\widehat{ADB}\) \(\left(M\in AB\right)\)
⇒ \(\dfrac{MA}{MB}=\dfrac{DA}{DB}\) (1)
b)
Δ\(ACD\) có \(AN\) là tia phân giác của \(\widehat{ADC}\) \(\left(N\in AC\right)\)
⇒ \(\dfrac{NA}{NC}=\dfrac{DA}{DC}\) (2)
Từ \(\left(1\right)và\left(2\right)\), mà \(BD=CD\left(gt\right)\)
⇒ \(\dfrac{MA}{MB}=\dfrac{NA}{NC}\)
⇒ \(MN\) // \(BC\) \(\left(ĐPCM\right)\)
c)
Δ\(ABC\) có \(MN\) // \(BC\) nên:
⇒ \(\dfrac{AM}{AB}=\dfrac{AN}{AC}\)
⇒ \(AM.AC=AN.AB\)
Ta có: \(MN\) //\(BC\)
⇒ \(\left\{{}\begin{matrix}\widehat{M_1}=\widehat{D_1}\\\widehat{N_1}=\widehat{D_4}\end{matrix}\right.\)
\(Mà\) \(\left\{{}\begin{matrix}\widehat{D_1}=\widehat{D_2}\\\widehat{D_3}=\widehat{D_4}\end{matrix}\right.\)
⇒ \(\left\{{}\begin{matrix}\widehat{M_1}=\widehat{D_2}\\\widehat{N_1}=\widehat{D_3}\end{matrix}\right.\)
Δ\(MKD\) có \(\widehat{M_1}=\widehat{D_2}\) ⇒ \(\text{Δ}MKD\) cân tại K
⇒ \(MK=KD\) \(\left(3\right)\)
Δ\(NKD\) có \(\widehat{N_1}=\widehat{D_3}\) ⇒ \(\text{Δ }NKD\) cân tại K
⇒ \(KN=KD\) \(\left(4\right)\)
Từ (3) và (4) ⇒ \(MK=KN\)
hay K là trung điểm của MN
Đúng 2
Bình luận (0)
Giúp e làm cái 26 vẽ hình giải chi tiết, 27 nua ạ
27:
=lim[n^3(-5-1/n+1/n^3)]=-vô cực
26B
Đúng 0
Bình luận (0)
giúp em giải giùm câu 5 d nha vẽ hình giùm ạ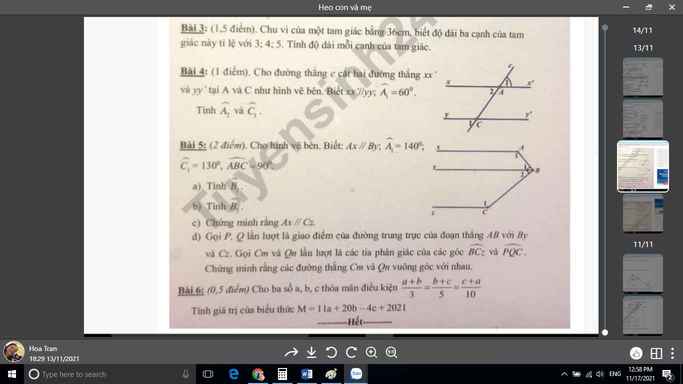
Vẽ giúp em một cái logo lớp 6/2 bắt mắt giùm em đi ạ em đang cần
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a , SA vuông góc vs (ABCD), SB=SD= a căn 5 , gọi M là trung điên của SD. Tính góc giữa 2 mp (AMC) và (ABCD). Nếu đc thì vẽ giùm mình cái hình luôn ạ. Cảm ơn rất nhiều...
Gọi O là tâm đáy \(\Rightarrow OD\perp AC\) (đường chéo hình vuông)
Gọi N là trung điểm AD \(\Rightarrow\) MN là đường trung bình tam giác SAD
\(\Rightarrow\left\{{}\begin{matrix}MN=\dfrac{1}{2}SA=\dfrac{a\sqrt{5}}{2}\\MN||SA\end{matrix}\right.\)
Do \(SA\perp\left(ABCD\right)\Rightarrow MN\perp\left(ABCD\right)\Rightarrow MN\perp AC\)
Gọi P là trung điểm AO \(\Rightarrow\) NP là đường trung bình tam giác OAD
\(\Rightarrow\left\{{}\begin{matrix}NP=\dfrac{1}{2}OD=\dfrac{a\sqrt[]{2}}{4}\\NP||OD\end{matrix}\right.\)
Mà \(OD\perp AC\Rightarrow NP\perp AC\)
\(\Rightarrow AC\perp\left(MNP\right)\)
Lại có AC là giao tuyến (AMC) và (ABCD)
\(\Rightarrow\widehat{MPN}\) là góc giữa (AMC) và (ABCD)
\(tan\widehat{MPN}=\dfrac{MN}{NP}=\sqrt{10}\Rightarrow\widehat{MPN}\approx72^027'\)
Đúng 0
Bình luận (0)
Cho hình thang vuông ABCD có góc A = Góc D = 90 độ. Trên Cạnh AD lấy các điểm E và F sao cho AE=BF và Góc BFC=90 độ . Chứng minh góc BEC = 90 độ
Không cần vẽ hình đâu ạ, giải chi tiết giùm em. Cảm ơn ạ
Bạn ơi, bạn xem lại đề xem thử có sai ở đâu không nha! Do nếu F nằm trên AD thì làm sao vẽ được góc BFC=90 độ được nhỉ?
Đúng 0
Bình luận (1)
Cho tam giác ABC vuông tại A. Kẻ đường cao AH. Gọi D, E là các hình chiếu của H trên AB, AC và M, N theo thứ tự là các trung điểm của các đoạn thẳng BH, CH.
Chứng minh tứ giác MDEN là hình thang vuông.
Giúp tớ bài này với ạ.... Khỏi vẽ hình cũng được. Tớ vẽ rồi
Cái bài nãy cũng có trên mạng mà giải chả hiểu gì cả
Mấy bạn giải giùm cụ thể. Tớ tick cho
19 tháng 1 2022 lúc 7:10
Cho \(\Delta\)\(ABC\) cân tại A. Trên tia đối của tia AB lấy điểm D, trên tia đối của tia AC lấy điểm E sao cho AD = AE. Chứng minh:
a) \(\Delta\)\(ADE\) cân
b) ED // BC
(Vẽ hình và làm hết giùm mk cái)
bn tự vẽ nha :
a, Xét \(\Delta ADE\)
có \(AD=AE\left(gt\right)\)
\(\Rightarrow\Delta ADE\) là tam giác cân
b, Xét \(\Delta ABC\) và \(\Delta ADE\) có :
\(AB=AD\left(gt\right)\)
\(\widehat{BAC}=\widehat{DAE}\) ( đối đỉnh )
\(AC=AE\left(gt\right)\)
\(\Rightarrow\Delta ABC=\Delta ADE\left(c.g.c\right)\)
\(\Rightarrow\widehat{EDA}=\widehat{ACB}\) ( hai góc tương ứng)
\(\Rightarrow ED\)//\(BC\)
Đúng 2
Bình luận (2)