d: =>6y+2-4x+4=5 và 15y+5-8x+8=9

=>-4x+6y=-1 và -8x+15y=-4

=>x=-3/4; y=-2/3

c: \(\Leftrightarrow\left\{{}\begin{matrix}x+1=-1\\y+1=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-2\\y=-3\end{matrix}\right.\)

b: \(\Leftrightarrow\left\{{}\begin{matrix}3y-15+2x-6=0\\7x-28+3y+3y-3=14\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x+3y=21\\7x+6y=45\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=\dfrac{19}{3}\end{matrix}\right.\)

a: \(=\dfrac{\left(x^4-y^4\right)^2}{x^2+y^2}=\left(x^2-y^2\right)^2\cdot\left(x^2+y^2\right)\)

b: \(=\dfrac{\left(4x+3\right)\left(16x^2-12x+9\right)}{16x^2-12x+9}=4x+3\)

a: Đặt |x-6|=a, |y+1|=b

Theo đề, ta có hệ phương trình:

\(\left\{{}\begin{matrix}2a+3b=5\\5a-4b=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=1\\b=1\end{matrix}\right.\)

=>|x-6|=1 và |y+1|=1

\(\Leftrightarrow\left\{{}\begin{matrix}x\in\left\{7;5\right\}\\y\in\left\{0;-2\right\}\end{matrix}\right.\)

b: Đặt |x+y|=a, |x-y|=b

Theo đề, ta có: \(\left\{{}\begin{matrix}2a-b=19\\3a+2b=17\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{55}{7}\\b=-\dfrac{23}{7}\left(loại\right)\end{matrix}\right.\)

=>HPTVN

c: Đặt |x+y|=a, |x-y|=b

Theo đề ta có: \(\left\{{}\begin{matrix}4a+3b=8\\3a-5b=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=2\\b=0\end{matrix}\right.\)

=>|x+y|=2 và x=y

=>|2x|=2 và x=y

=>x=y=1 hoặc x=y=-1

\(c,P=\dfrac{x^2-x^2+8xy-16y^2}{x^2+4y^2}=\dfrac{8\left(\dfrac{x}{y}\right)-16}{\left(\dfrac{x}{y}\right)^2+4}\)

Đặt \(\dfrac{x}{y}=t\)

\(\Leftrightarrow P=\dfrac{8t-16}{t^2+4}\Leftrightarrow Pt^2+4P=8t-16\\ \Leftrightarrow Pt^2-8t+4P+16=0\)

Với \(P=0\Leftrightarrow t=2\)

Với \(P\ne0\Leftrightarrow\Delta'=16-P\left(4P+16\right)\ge0\)

\(\Leftrightarrow-P^2-4P+4\ge0\Leftrightarrow-2-2\sqrt{2}\le P\le-2+2\sqrt{2}\)

Vậy \(P_{max}=-2+2\sqrt{2}\Leftrightarrow t=\dfrac{4}{P}=\dfrac{4}{-2+2\sqrt{2}}=2+\sqrt{2}\)

\(\Leftrightarrow\dfrac{x}{y}=2+2\sqrt{2}\)

Bài a hình như sai đề rồi bạn.

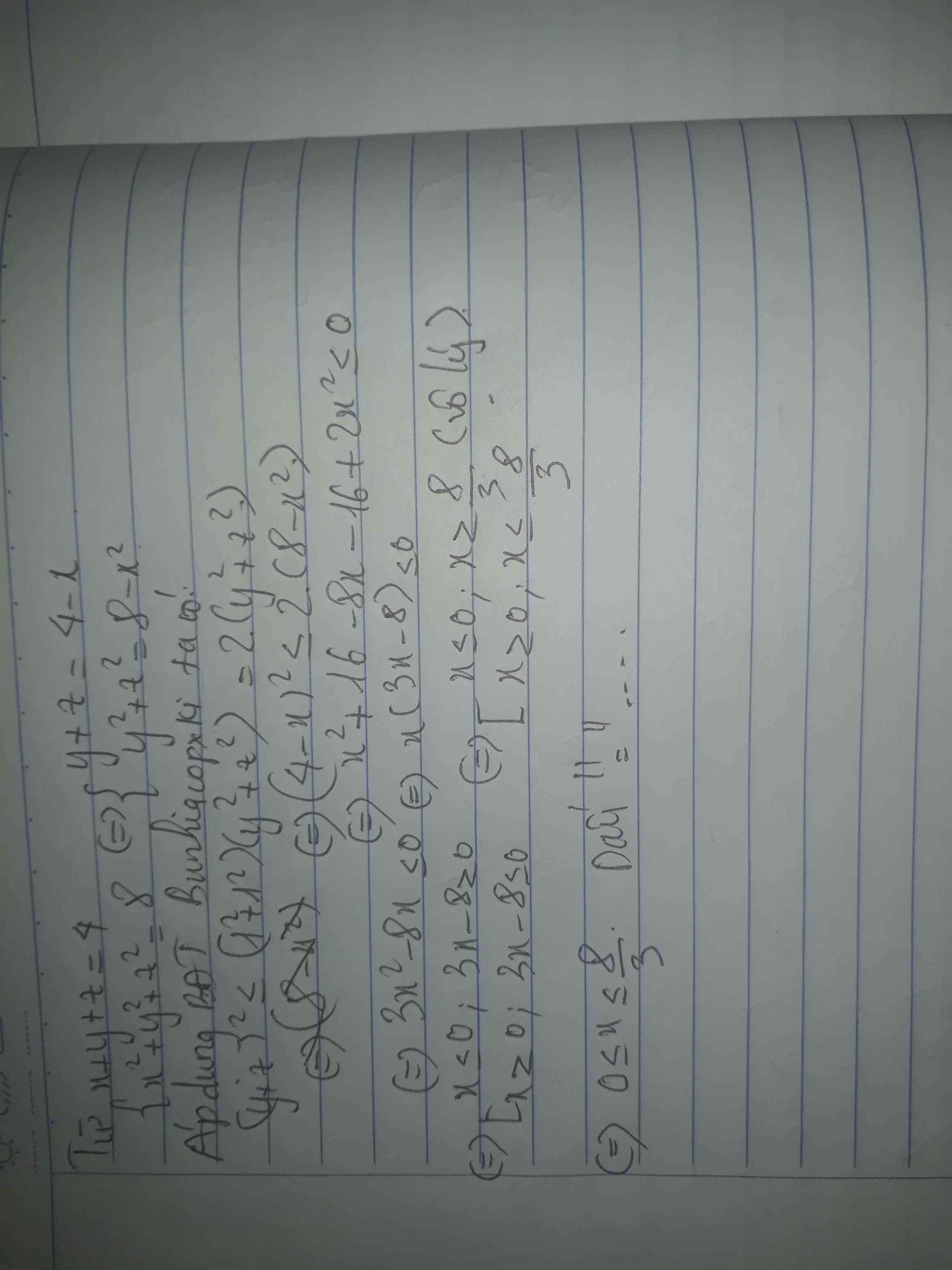
\(a,\text{Đặt }\left\{{}\begin{matrix}S=y+z\\P=yz\end{matrix}\right.\\ HPT\Leftrightarrow\left\{{}\begin{matrix}\left(y+z\right)^2-2yz+x^2=8\\x\left(y+z\right)+yz=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}S^2-2P+x^2=8\\Sx+P=4\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}S^2-2\left(4-Sx\right)+x^2=8\\P=4-Sx\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}S^2+2Sx+x^2-16=0\left(1\right)\\P=4-Sx\end{matrix}\right.\\ \left(1\right)\Leftrightarrow\left(S+x-4\right)\left(S+x+4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}S=-x+4\Rightarrow P=\left(x-2\right)^2\\S=-x-4\Rightarrow P=\left(x+2\right)^2\end{matrix}\right.\)

Mà y,z là nghiệm của hệ nên \(S^2-4P\ge0\Leftrightarrow\left[{}\begin{matrix}\left(4-x\right)^2\ge4\left(x-2\right)^2\\\left(-4-x\right)^2\ge4\left(x+2\right)^2\end{matrix}\right.\Leftrightarrow-\dfrac{8}{3}\le x\le\dfrac{8}{3}\)

1) a) \(\left|7x-5y\right|+\left|2z-3y\right|+\left|xy+yz+xz-2000\right|\ge0\)

Dấu "=" xảy ra khi: \(\left\{{}\begin{matrix}7x=5y\\2z=3y\\xy+yz+xz=2000\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=\dfrac{5}{7}y\\z=\dfrac{3}{2}y\\xy+yz+xz=2000\end{matrix}\right.\)

Ta có: \(xy+yz+xz=2000\)

\(\Rightarrow\dfrac{5}{7}y^2+\dfrac{3}{2}y^2+\dfrac{15}{14}y^2=2000\)

\(\Rightarrow y^2\left(\dfrac{5}{7}+\dfrac{3}{2}+\dfrac{15}{14}\right)=2000\Leftrightarrow\dfrac{23}{7}y^2=2000\)

Tìm \(y\) và suy ra \(x;z\) là được,Bài này nghiệm khá xấu

b) \(\left|3x-7\right|+\left|3x+2\right|+8=\left|7-3x\right|+\left|3x+2\right|+8\ge\left|7-3x+3x+2\right|+8\ge9+8=17\)Dấu "=" xảy ra khi: \(-\dfrac{3}{2}\le x\le\dfrac{7}{3}\)

2) a)Ta có: \(\left\{{}\begin{matrix}\left|x-5\right|+\left|1-x\right|\ge\left|x-5+1-x\right|=4\\\dfrac{12}{\left|y+1\right|+3}\le\dfrac{12}{3}=4\end{matrix}\right.\)

Mà theo đề bài: \(\left|x-5\right|+\left|1-x\right|=\dfrac{12}{\left|y+1\right|+3}\)

\(\Rightarrow\left|x-5\right|+\left|1-x\right|=\dfrac{12}{\left|y+1\right|+3}=4\)

\(\Rightarrow\left\{{}\begin{matrix}1\le x\le5\\y=-1\end{matrix}\right.\)

b) Ta có: \(\left\{{}\begin{matrix}\left|y+3\right|+5\ge5\\\dfrac{10}{\left(2x-6\right)^2+2}\le\dfrac{10}{2}=5\end{matrix}\right.\)

Mà theo đề bài: \(\left|y+3\right|+5=\dfrac{10}{\left(2x-6\right)^2+2}\)

\(\Rightarrow\left|y+3\right|+5=\dfrac{10}{\left(2x-6\right)^2+2}=5\)

\(\Rightarrow\left\{{}\begin{matrix}y=-3\\x=3\end{matrix}\right.\)

c) Ta có: \(\left\{{}\begin{matrix}\left|x-1\right|+\left|3-x\right|\ge\left|x-1+3-x\right|=2\\\dfrac{6}{\left|y+3\right|+3}\le\dfrac{6}{3}=2\end{matrix}\right.\)

Mà theo đề bài: \(\left|x-1\right|+\left|3-x\right|=\dfrac{6}{\left|y+3\right|+3}\)

\(\Rightarrow\left|x-1\right|+\left|3-x\right|=\dfrac{6}{\left|y+3\right|+3}=2\)

\(\Rightarrow\left\{{}\begin{matrix}1\le x\le3\\y=-3\end{matrix}\right.\)

\(A=x^3.\left(-\dfrac{5}{4}x^2y\right).\left(\dfrac{2}{5}x^3y^4\right).\\ A=-\dfrac{1}{2}x^8y^5.\)

- Bậc: 8.

- Hệ số: \(-\dfrac{1}{2}.\)

- Biến: \(x;y.\)

\(B=\left(-\dfrac{3}{4}x^5y^4\right).\left(xy^2\right).\left(-\dfrac{8}{9}x^2y^3\right).\\ B=\dfrac{2}{3}x^8y^9.\)

- Bậc: 9.

- Hệ số: \(\dfrac{2}{3}.\)

- Biến: \(x;y.\)

a: \(=4x^2-25-4x^2+12x-9-12x=-34\)

b: \(=8y^3-12y^2+6y-1-2y\left(4y^2-12y+9\right)-12y^2+12y\)

\(=8y^3-24y^2+18y-1-8y^3+24y^2-18y=-1\)

c: \(=x^3+27-x^3-20=7\)

d: \(=3y\left(9y^2+12y+4\right)-27y^3+1-36y^2-12y-1\)

\(=27y^3+36y^2+12y-27y^3-36y^2-12y\)

=0

a) =(x-y)⁵+(x-y)³=(x-y)³[(x-y)²+1]

b) =3³(y-2x)³:-9(y-2x)=-3(y-2x)²

c) =(x-y)² [3(x-y)³-2(x-y)²+3]:5(x-y)²=[3(x-y)³-2(x-y)²+3]/5