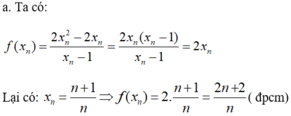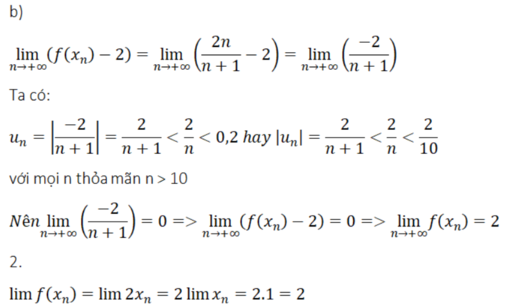xn (2xn-3 - 5) - 2xn (xn-3 + 4)

Những câu hỏi liên quan
Cho dãy (xn) thỏa 1<xn<2 và xn+1=1+xn-1/2xn^2 với mọi n thuộc N
a,chứng minh |xn-căn 2|<(1/2)^n với mọi n lớn hơn hoặc bằng 3
b,Tính lim xn
Cho dãy số
x
n
xác định bởi:
x
1
0
3
n
+
2
x
n
+...
Đọc tiếp
Cho dãy số x n xác định bởi:
x 1 > 0 3 n + 2 x n + 1 2 = 2 n + 1 x n + 1 2 + n + 4 ∀ n ≥ 21
Hãy tìm l i m x n
A. 0
B. 1
C. 2
D. 3
Ta có:
3 n + 2 x n + 1 2 = 2 n + 1 x n + 1 2 + n + 4 ∀ n ≥ 21
⇔ 3 n + 2 x n + 1 2 = 2 n + 1 x n + 1 2 - 2 n + 1 + 3 n - 2 , ∀ n ≥ 21 ⇔ 3 n + 2 x n + 1 2 - 1 = 2 n + 1 x n 2 - 1
Đặt y n = x n 2 - 1 . Khi đó
y n + 1 = 2 3 . n + 1 n + 2 y n
Suy ra
y n + 1 = 2 n + 1 3 n + 2 . 2 n 3 n + 1 = 2 3 n + 1 . 1 n + 2 y 1
hay l i m y n = 0 . Vậy l i m x n = 1
Đáp án cần chọn là B
Đúng 0
Bình luận (0)
Bài 5: Làm tính nhân
a) 4x4.( 7xn-1+x-5)
b) 2xn-2.(14xn+1-10x2)
c) 2n-1.(xn-1+2)
a) 4x⁴.(xⁿ⁻¹ + x - 5)
= 4xⁿ⁺³ + 4x⁵ - 20x⁴
b) 2xⁿ⁻².(14xⁿ⁺¹ - 10x²)
= 28x²ⁿ⁻¹ - 20xⁿ
c) 2ⁿ⁻¹.(xⁿ⁻¹ + 2)
= (2x)ⁿ⁻¹ + 2ⁿ
Đúng 1
Bình luận (0)
Mn ơi cho mik hỏi câu này đc ko ạ ?
( - x2y3)( 2xn-2yn - 3xnyn-3 + xn-2 yn-3 )
Biết n thuộc N , n lớn hơn hoặc bằng 3
Mik cảm ơn !
\(=-x^2y^3\cdot2x^{n-2}y^n+x^2y^3\cdot3x^ny^{n-3}-x^2y^3\cdot x^{n-2}y^{n-3}\)
\(=-2x^ny^{n+3}+3x^{n+2}y^n-x^ny^n\)
Đúng 0
Bình luận (0)
Tìm n thỏa mãn
A, 2+4+6+...+2xn=210. B, 1+3+5+....+(2xn-1)=225
a, 2 + 4 + 6 +...+ 2 \(\times\) n = 210
A = 2 + 4 + 6 +...+ 2n
Dãy số trên là dãy số cách đều với khoảng cách là: 4 - 2 = 2.
Số số hạng của dãy số trên là: (2n - 2): 2 + 1 = n
A = (2n + 2).n : 2 = (n+1).n
⇒ (n+1).n = 210 ⇒ (n+1).n = 14 \(\times\) 15 ⇒ n = 14
Đúng 1
Bình luận (0)
B, 1 + 3 + 5+...+ (2n - 1) = 225
B = 1 + 3 + 5 +...+ (2n - 1)
Dãy số trên là dãy số cách đều với khoảng cách là: 3 - 1 = 2
Số số hạng của dãy số trên là: ( 2n - 1 - 1): 2 + 1 = n
B = (2n - 1+1).n : 2 = n.n
⇒n2 = 225 ⇒ n2 = 152 ⇒ \(\left[{}\begin{matrix}n=15\\n=-15\end{matrix}\right.\); n = -15 loại
Vậy n = 15
Đúng 1
Bình luận (0)
A) \(2+4+6+...+2n=210\)
\(\Rightarrow\left(\left(2n-2\right):2+1\right)\left(2n+2\right):2=210\)
\(\Rightarrow\left(2\left(n-1\right):2+1\right)2.\left(n+1\right)=210.2\)
\(\Rightarrow2\left(n-1+1\right)\left(n+1\right)=420\)
\(\Rightarrow n\left(n+1\right)=210\)
\(\Rightarrow n^2+n-210=0\)
\(\Rightarrow\left(n-14\right)\left(n+15\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}n-14=0\\n+15=0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}n=14\\n=-15\end{matrix}\right.\) \(\Rightarrow n\in\left\{14;-15\right\}\left(n\in Z\right)\)
B) \(1+3+5+...+\left(2n-1\right)=225\)
\(\Rightarrow\left(\left(2n-1-1\right):2+1\right)\left(2n-1+1\right):2=225\)
\(\Rightarrow\left(\left(2n-2\right):2+1\right).2n=225.2\)
\(\Rightarrow\left(2\left(n-2\right):2+1\right).2n=450\)
\(\Rightarrow\left(n-1+1\right).2n=450\)
\(\Rightarrow n.2n=450\Rightarrow n^2=450:2=225\)
\(\Rightarrow n^2=15^2\Rightarrow n=15\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Xét hàm số
f
x
2
x
2
-
2
x
x
-
1
1. Cho biến x những giá trị khác 1 lập thành dãy số
x
n
,
x
n...
Đọc tiếp
Xét hàm số f x = 2 x 2 - 2 x x - 1
1. Cho biến x những giá trị khác 1 lập thành dãy số x n , x n → 1 như trong bảng sau:

Khi đó, các giá trị tương ứng của hàm số
f ( x 1 ) , f ( x 2 ) , … , f ( x n ) , …
cũng lập thành một dãy số mà ta kí hiệu là f ( x n ) .
a) Chứng minh rằng f ( x n ) = 2 x n = ( 2 n + 2 ) / n .
b) Tìm giới hạn của dãy số f ( x n ) .
2. Chứng minh rằng với dãy số bất kì x n , x n ≠ 1 và x n → 1 , ta luôn có f ( x n ) → 2 .
(Với tính chất thể hiện trong câu 2, ta nói hàm số f x = 2 x 2 - 2 x x - 1 có giới hạn là 2 khi x dần tới 1).
Chứng minh rằng phân số \(\frac{2xn+3}{2xn+4}\) tối giản với mọi n \(\varepsilon\) N
3xn-1/2xn-3
5(3xn+1-yn-1)-3(xn+1+2yn-1)+4(-xn+1+2yn-1)
\(5\left(3x^{n+1}-y^{n-1}\right)-3\left(x^{n+1}+2y^{n-1}\right)+4\left(-x^{n+1}+2y^{n-1}\right)\)
\(=15x^{n+1}-5y^{n-1}-3x^{n+1}-6y^{n-1}-4x^{n+1}+8y^{n-1}\)
\(=8x^{n+1}-3y^{n-1}\)
Đúng 2
Bình luận (0)
Tìm số tự nhiên n , biết :
1+3+5+7+....+(2xn - 1) = 169