Tìm giá trị nhỏ nhất của biểu thức C = x2 + 2y2 – 2xy – 4y + 5

Những câu hỏi liên quan
Tìm giá trị nhỏ nhất của biểu thức: A=x2-2xy+2y2-4y+5
\(A=x^2-2xy+2y^2-4y+5\\=(x^2-2xy+y^2)+(y^2-4y+4)+1\\=(x-y)^2+(y-2)^2+1\)
Ta thấy: \(\left(x-y\right)^2\ge0\forall x;y\)
\(\left(y-2\right)^2\ge0\forall y\)
\(\Rightarrow\left(x-y\right)^2+\left(y-2\right)^2\ge0\forall x;y\)
\(\Rightarrow A=\left(x-y\right)^2+\left(y-2\right)^2+1\ge1\forall x;y\)
Dấu \("="\) xảy ra khi: \(\left\{{}\begin{matrix}x-y=0\\y-2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=y\\y=2\end{matrix}\right.\)
\(\Leftrightarrow x=y=2\)
Vậy \(Min_A=1\) khi \(x=y=2\).
$Toru$
Đúng 2
Bình luận (0)
Tìm giá trị nhỏ nhất của biểu thức C = x2 + 2y2 – 2xy – 4y + 5
\(C=x^2+2y^2-2xy-4y+5=\left(x^2-2xy+y^2\right)+\left(y^2-4y+4\right)+1\)
\(=\left(x-y\right)^2+\left(y-2\right)^2+1\ge1\)
Đẳng thức xảy ra khi x = y = 2
Vậy min C = 1 khi x = y = 2
Đúng 0
Bình luận (0)
Ta có : C = (x2 - 2xy + y2) + ( y2 – 4y+4)+1 = (x –y)2 + (y -2)2 + 1 Vì (x – y)2 ≥ 0 ; (y-2)2 ≥ 0 Do vậy: C ≥ 1 với mọi x;y Dấu “ = ” Xảy ra khi x-y = 0 và y-2 =0 ⇔ x=y =2Vậy: Min C = 1 khi x = y =2
Đúng 0
Bình luận (0)
Tìm giá trị nhỏ nhất của biểu thức A = x 2 + 2 y 2 – 2xy + 2x – 10y
A. A = 3
B. A = -17
C. A = -3
D. A = 17
A = x 2 + 2 y 2 – 2 x y + 2 x – 10 y ⇔ A = x 2 + y 2 + 1 – 2 x y + 2 x – 2 y + y 2 – 8 y + 16 – 17 ⇔ A = ( x 2 + y 2 + 12 – 2 . x . y + 2 . x . 1 – 2 . y . 1 ) + ( y 2 – 2 . 4 . y + 4 2 ) – 17 ⇔ A = ( x – y + 1 ) 2 + ( y – 4 ) 2 – 17
Vì với mọi x; y nên A ≥ -17 với mọi x; y
=> A = -17
⇔ x − y + 1 = 0 y − 4 = 0 ⇔ x = y − 1 y = 4 ⇔ x = 3 y = 4
Vậy A đạt giá trị nhỏ nhất là A = -17 tại x = 3 y = 4
Đáp án cần chọn là: B
Đúng 1
Bình luận (0)
Tìm giá trị nhỏ nhất của biểu thức A = x 2 + 2 y 2 – 2xy + 2x – 10y
A. 17
B. 0
C. -17
D. -10
A = x 2 + 2 y 2 – 2 x y + 2 x – 10 y ⇔ A = x 2 + y 2 + 1 – 2 x y + 2 x – 2 y + y 2 – 8 y + 16 – 17 ⇔ A = ( x 2 + y 2 + 1 2 – 2 . x . y + 2 . x . 1 – 2 . y . 1 ) + ( y 2 – 2 . 4 . y + 4 2 ) – 17 ⇔ A = ( x – y + 1 ) 2 + ( y – 4 ) 2 – 17
Vì x - y + 1 2 ≥ 0 y - 4 2 ≥ 0 với mọi x, y nên A ≥ -17 với mọi x, y
=> A = -17 ó x - y + 1 = 0 y - 4 = 0 ó x = y - 1 y = 4 ó x = 3 y = 4
Vậy A đạt giá trị nhỏ nhất là A = -17 tại x = 3 y = 4
Đáp án cần chọn là: C
Đúng 1
Bình luận (0)
tìm giá trị nhỏ nhất của biểu thức A = x2 + 2y2 – 2xy + 2x – 10y
\(A=\left[\left(x^2-2xy+y^2\right)+2\left(x-y\right)+1\right]+\left(y^2-8y+16\right)-17\\ A=\left(x-y+1\right)^2+\left(y-4\right)^2-17\ge-17\)
Dấu \("="\Leftrightarrow\left\{{}\begin{matrix}x-y+1=0\\y-4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=y-1=3\\y=4\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Tìm giá trị nhỏ nhất của biểu thức: Q = x 2 + 2 y 2 + 2 x y − 2 x − 6 y + 2015
Q = x 2 + 2 y 2 + 2 x y − 2 x − 6 y + 2015 = x 2 + 2 x y + y 2 − 2 x − 2 y + 1 + y 2 − 4 y + 4 + 2010 = x 2 + 2 x y + y 2 − 2 x + 2 y + 1 + y 2 − 4 y + 4 + 2010 = x + y 2 − 2 x + y + 1 + y 2 − 4 y + 4 + 2010 = x + y − 1 2 + y − 2 2 + 2010
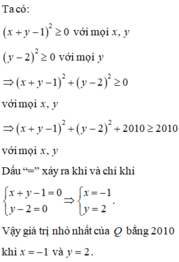
Đúng 0
Bình luận (0)
Tìm giá trị nhỏ nhất của biểu thức P x2 + 2y2 + 2xy – 6x – 8y + 2028
Đọc tiếp
Tìm giá trị nhỏ nhất của biểu thức P = x2 + 2y2 + 2xy – 6x – 8y + 2028
Lời giải:
$P=(x^2+y^2+2xy)+y^2-6x-8y+2028$
$=(x+y)^2-6(x+y)+(y^2-2y)+2028$
$=(x+y)^2-6(x+y)+9+(y^2-2y+1)+2018$
$=(x+y-3)^2+(y-1)^2+2018\geq 0+0+2018=2018$
Vậy $P_{\min}=2018$
Giá trị này đạt tại $x+y-3=y-1=0$
$\Leftrightarrow y=1; x=2$
Đúng 1
Bình luận (0)
Tìm giá trị nhỏ nhất của biểu thức:
Q=x2+2y2+2z2+2xy-2yz-2xz-2y+4z+5
\(Q=x^2+2y^2+2z^2+2xy-2yz-2xz-2y+4z+5=\left[\left(x^2+2xy+y^2\right)-2z\left(x+y\right)+z^2\right]+\left(y^2-2y+1\right)+\left(z^2+4z+4\right)=\left(x+y-z\right)^2+\left(y-1\right)^2+\left(z+2\right)^2\ge0\)
\(minQ=0\Leftrightarrow\)\(\left\{{}\begin{matrix}x=-3\\y=1\\z=-2\end{matrix}\right.\)
Đúng 1
Bình luận (0)
`Q=x^2+2y^2+2z^2+2xy-2yz-2xz-2y+4z+5`
`Q=(x^2+y^2-z^2+2xy-2yz-2xz)+(y^2-2y+1)+(z^2+4z+4)`
`Q=(x+y-z)^2+(y-1)^2+(z+2)^2`
Ta thấy :
`(x+y-z)^2>=0`
`(y-1)^2>=0`
`(z+2)^2>=0`
`=>(x+y-z)^2+(y-1)^2+(z+2)^2>=0`
Dấu = xảy ra
`<=>` $\begin{cases}x+y-z=0\\y-1=0\\z+2=0\end{cases}$
`<=>` $\begin{cases}x=-3\\y=1\\z=-2\end{cases}$
Đúng 0
Bình luận (0)
Tìm giá trị nhỏ nhất của biểu thức
A= x2 + 2y2 - 2xy + 2x - 10y
\(A=\left(x^2-2xy+y^2\right)+2\left(x-y\right)+1+y^2-8y+16-17\\ A=\left(x-y+1\right)^2+\left(y-4\right)^2-16\ge17\)
Vậy \(A_{min}=17\leftrightarrow\left\{{}\begin{matrix}x-y+1=0\\y-4=0\end{matrix}\right.\leftrightarrow\left\{{}\begin{matrix}x=3\\y=4\end{matrix}\right.\)
Đúng 4
Bình luận (0)




















