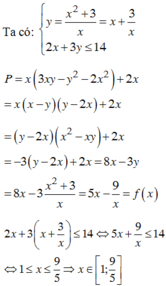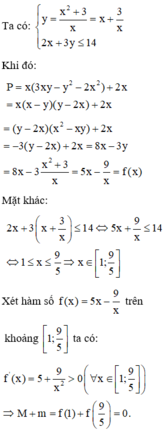Tính giá trị biểu thức sau: C=xy2−x2+x√−2y2C=xy2−x2+x−2y2 với x=202y–232;y=25y–1029x=202y–232;y=25y–1029 Làm tròn đến 4 chữ số thập phân

Những câu hỏi liên quan
Tính giá trị của biểu thức C tại x=2 ; y=-1 biết 2xy2 - 3xy + x2 -4 - C = xy2 - x2 + 2y2 + 1
\(2xy^2-3xy+x^2-4-C=xy^2-x^2+2y^2+1\)
\(\Rightarrow C=2xy^2-3xy+x^2-4-\left(xy^2-x^2+2y^2+1\right)\)
\(=2xy^2-3xy+x^2-4-xy^2+x^2-2y^2-1\)
\(=xy^2-3xy+2x^2-2y^2-5\)
Thay x = 2 và y = -1 vào C ta được :
\(C=2.\left(-1\right)^2-3.2.\left(-1\right)+2.2^2-2.\left(-1\right)^2-5=9\)
Vậy : Khi x = 2 và y = -1 thì giá trị của C là -9.
Đúng 1
Bình luận (0)
bài 2: rút gọn các biểu thức sau :
a,(3 - xy2)2 - (2 + xy2) 2
b, (x - y) (x2 + xy +y 2 )
c, ( x - 3 )3 + (2 - x )3
a) \(\left(3-xy^2\right)^2-\left(2+xy^2\right)^2\)
\(=\left(3-xy^2+2+xy^2\right)\left(3-xy^2-2-xy^2\right)\)
\(=5.\left(-2xy^2\right)\)
\(=-10xy^2\)
b) \(\left(x-y\right)\left(x^2+xy+y^2\right)\)
\(=x^3-y^3\)
c) \(\left(x-3\right)^3+\left(2-x\right)^3\)
\(=x^3-3x^2.3+3x.3^2-3^3+2^3-3.2^2.x+3.2.x^2-x^3\)
\(=x^3-9x^2+27x-27+8-12x+6x^2-x^3\)
\(=\left(x^3-x^3\right)+\left(-9x^2+6x^2\right)+\left(27x-12x\right)+\left(-27+8\right)\)
\(=-3x^2+15x-19\)
Đúng 2
Bình luận (0)
Tính giá trị các biểu thức sau:
1/ 3x4 + 5x2y2 + 2y4 + 2y2 biết rằng x2 + y2 = 2
2/ 7x - 7y + 4ax - 4ay - 5 biết x - y = 0
3/ x3 + xy2 - x2y - y3 + 3 biết x - y = 0
4/ x2 + 2xy + y2 - 4x - 4y + 1 biết rằng x + y = 3
Giúp mình bài này với
Bài 3* : Tính giá trị các biểu thức sau:
a) 3x4 + 5x2y2 + 2y4 + y2 biết rằng x2 + y2 = 1
b) 7x - 7y + 4ax - 4ay - 5 biết x - y = 0
c) x3 + xy2 - x2y - y3 + 3 biết x - y = 0
d) x2 + 2xy + y2 - 4x - 4y + 1 biết rằng x + y = 3
a: \(=3x^4+3x^2y^2+2x^2y^2+2y^4+y^2\)
\(=\left(x^2+y^2\right)\left(3x^2+2y^2\right)+y^2\)
\(=3x^2+3y^2=3\)
b: \(=7\left(x-y\right)+4a\left(x-y\right)-5=-5\)
c: \(=\left(x-y\right)\left(x^2+xy+y^2\right)+xy\left(y-x\right)+3=3\)
d: \(=\left(x+y\right)^2-4\left(x+y\right)+1\)
=9-12+1
=-2
Đúng 1
Bình luận (0)
Cho x,y0 và thỏa mãn
x
2
-
x
y
+
3
0
2
x
+
3
y
-...
Đọc tiếp
Cho x,y>0 và thỏa mãn x 2 - x y + 3 = 0 2 x + 3 y - 14 ≤ 0 . Tính tổng giá trị lớn nhất và nhỏ nhất của biểu thức P = 3 x 2 y - x y 2 - 2 x 3 + 2 x ?
A. 8
B. 0
C. 4
D. 12
Ta có:
x 2 - x y + 3 = 0 1 2 x + 3 y - 14 ≤ 0 2
Do x,y>0 nên ⇔ x 2 + 3 x thay vào (2) ta được:
2 x + 3 . x 2 + 3 x - 14 ≤ 0
⇔ 2 x 2 + 3 x 2 + 9 - 14 x x ≤ 0
⇔ 5 x 2 - 14 x + 9 ≤ 0 ⇔ 1 ≤ x ≤ 9 5
Thay y = x 2 + 3 x vào P ta được:
P = 3 x 2 y - x y 2 - 2 x 3 + 2 x
= 3 x 2 . x 2 + 3 x - x . x 2 + 3 x 2 - 2 x 3 + 2 x
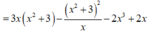
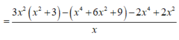
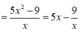
P ' = 5 + 9 x 2 > 0 với mọi x nên hàm số P=P(x) đồng biến trên 1 ; 9 5
Vậy 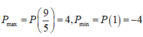
Tổng ![]() .
.
Chọn đáp án B.
Đúng 0
Bình luận (0)
Cho x,y 0 và thỏa mãn
x
2
-
x
y
+
3
0
2
x
+
2
y
-...
Đọc tiếp
Cho x,y > 0 và thỏa mãn x 2 - x y + 3 = 0 2 x + 2 y - 14 ≤ 0 .Tính tổng giá trị lớn nhất và nhỏ nhất của biểu thức P = 3 x 2 y - x y 2 - 2 x 3 + 2 x
A. 4.
B. 8.
C. 12.
D. 0.
Cho
x
,
y
0
và thỏa mãn
x
2
−
x
y
+
3
0
2
x
+
3...
Đọc tiếp
Cho x , y > 0 và thỏa mãn x 2 − x y + 3 = 0 2 x + 3 y − 14 ≤ 0 . Tính tổng giá trị lớn nhất và nhỏ nhất của biểu thức P = 3 x 2 y − x y 2 − 2 x 3 + 2 x ?
A. 4
B. 8
C. 12
D. 0
Cho
x
,
y
0
và thỏa mãn
x
2
-
x
y
+
3
0
2
x
+
3...
Đọc tiếp
Cho x , y > 0 và thỏa mãn x 2 - x y + 3 = 0 2 x + 3 y - 14 ≤ 0 . Tính tổng giá trị lớn nhất và nhỏ nhất của biểu thức P = 3 x 2 y - x y 2 - 2 x 3 + 2 x ?
A. 8
B. 0
C. 4
D. 12
Đáp án B
Phương pháp:
- Rút y từ phương trình đầu, thay vào bất phương trình sau tìm điều kiện của x .
- Thay y ở trên vào biểu thức P đưa về biến x .
- Sử dụng phương pháp hàm số đánh giá P tìm GTLN, GTNN.
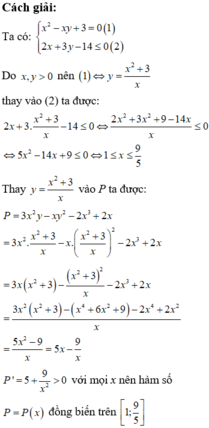
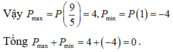
Đúng 0
Bình luận (0)
biểu thức nào trong các biểu thức sau đây là đơn thức
A 2y2
B x+ 4y
c. x-y
D xy2