Question

Cho x,y>0 và thỏa mãn x 2 - x y + 3 = 0 2 x + 3 y - 14 ≤ 0 . Tính tổng giá trị lớn nhất và nhỏ nhất của biểu thức  P = 3 x 2 y - x y 2 - 2 x 3 + 2 x ?

A. 8

B. 0

C. 4

D. 12

Answer 1

Ta có:

x 2 - x y + 3 = 0 1 2 x + 3 y - 14 ≤ 0 2

Do x,y>0 nên ⇔ x 2 + 3 x  thay vào (2) ta được:

2 x + 3 . x 2 + 3 x - 14 ≤ 0

⇔ 2 x 2 + 3 x 2 + 9 - 14 x x ≤ 0

⇔ 5 x 2 - 14 x + 9 ≤ 0 ⇔ 1 ≤ x ≤ 9 5

Thay y = x 2 + 3 x  vào P ta được:

P = 3 x 2 y - x y 2 - 2 x 3 + 2 x

= 3 x 2 . x 2 + 3 x - x . x 2 + 3 x 2 - 2 x 3 + 2 x

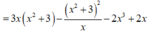
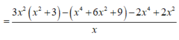
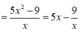
P ' = 5 + 9 x 2 > 0  với mọi x nên hàm số P=P(x) đồng biến trên  1 ; 9 5

Vậy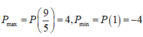 

Tổng .

Chọn đáp án B.