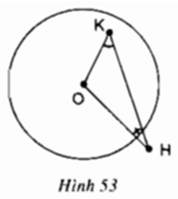
Từ điểm K nằm ngoài đường tròn (O;R), vẽ tiếp tuyến KA và KB với đường tròn (với A, B là tiếp điểm ).
a, Chứng minh tứ giác KAOB là tứ giác nội tiếp
b, Gọi M là trung điểm của AK. Đoạn thẳng BM cắt (O) tại điểm thứ hai là N. Đường thẳng KN cắt (O) tại điểm thứ hai là D . Chứng minh AK \(//\)BD