giải dùm em em tick hết

Những câu hỏi liên quan
Giải dùm em hết với ạ,em đang cần qấp, em cảm ơn ạ !

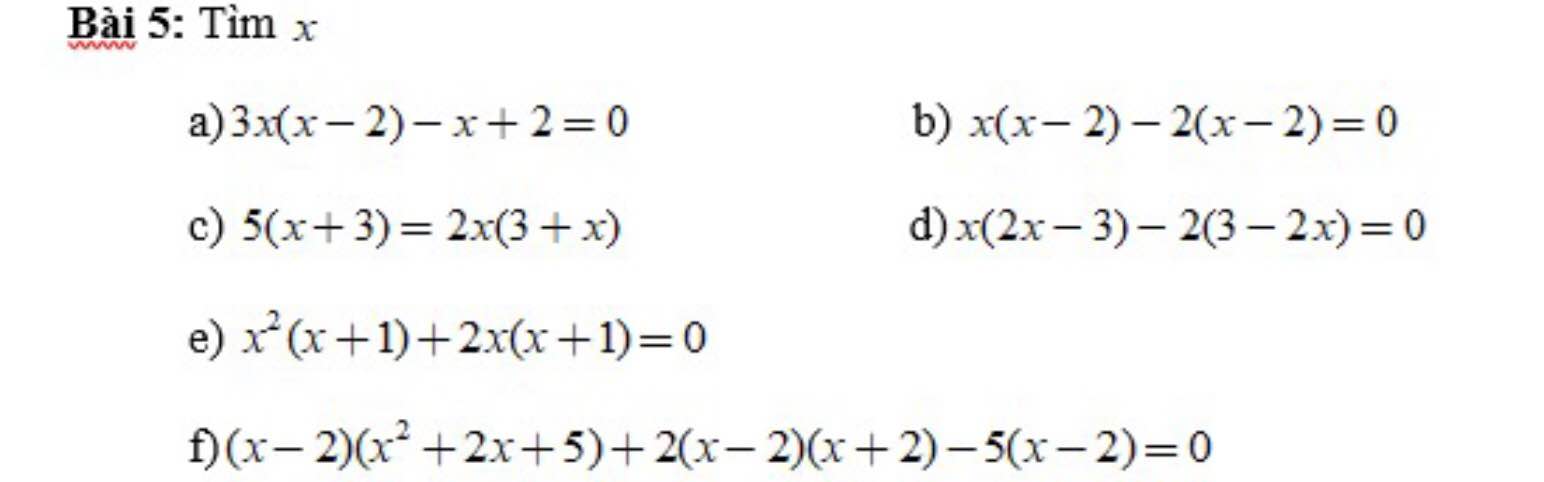 giải hết dùm em nha
giải hết dùm em nha
a) \(3x\left(x-2\right)-x+2=0\)
\(3x\left(x-2\right)-\left(x-2\right)=0\)
\(\left(x-2\right)\left(3x-1\right)=0\)
⇔\(\left[{}\begin{matrix}x-2=0\\3x-1=0\end{matrix}\right.\)
⇔\(\left[{}\begin{matrix}x=2\\x=\dfrac{1}{3}\end{matrix}\right.\)
b) \(x\left(x-2\right)-2\left(x-2\right)=0\)
\(\left(x-2\right)\left(x-2\right)=0\)
\(\left(x-2\right)^2=0\)
⇔\(x-2=0\)
⇔\(x=2\)
Đúng 0
Bình luận (0)
1. Tìm x, y biết :
x57y chia hết cho 15
2 .Tìm chữ số tận cùng của B, biết :
B= 3+3 mủ3 + 3 mủ5+ ......+ 3 mủ 2017
Mong mọi người giải dùm em ak . Em sẽ tick ạ !
giải dùm em s ạ
có gì giải thích dùm em luôn em cảm ơn nhiều

14.
\(y'=2x^3-4x=2x\left(x^2-2\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\x=-\sqrt{2}\\x=\sqrt{2}\end{matrix}\right.\)
\(y''=6x-4\)
\(\Rightarrow y''\left(0\right)=-4< 0\Rightarrow x=0\) là điểm cực đại
\(y\left(0\right)=-3\)
\(\Rightarrow\) Điểm cực đại của đồ thị hàm số là \(\left(0;-3\right)\)
Đúng 1
Bình luận (0)
12.
\(y'=3x^2-3=0\Rightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)
\(y''=6x\)
\(\Rightarrow\left\{{}\begin{matrix}y''\left(1\right)=6>0\\y''\left(-1\right)=-6< 0\end{matrix}\right.\) \(\Rightarrow x=-1\) là điểm cực đại
\(\Rightarrow\)Giá trị cực đại của hàm số là \(y\left(-1\right)=3\)
Đúng 1
Bình luận (0)
2.
\(y'=x^2-2mx+m^2-m+1\)
\(y''=2x-2m\)
Hàm đạt cực đại tại \(x=1\) khi:
\(\left\{{}\begin{matrix}y'\left(1\right)=0\\y''\left(1\right)< 0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m^2-3m+2=0\\2-2m< 0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m=1\\m=2\end{matrix}\right.\\m>1\end{matrix}\right.\) \(\Rightarrow m=2\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Giải dùm em ạ lời giải chi tiết dùm em ạ 
Gọi số học sinh nam là x
Số học sinh nữ là 32-x
Vì khi chuyển 4 nữ đi thì số nam và số nữ bằng nhau nên ta có:
32-x-4=x
=>28-x=x
=>x=14
Vậy: Có 14 nam và 18 nữ
Đúng 2
Bình luận (0)
Giải dùm em với ạ
 giải dùm em voi
giải dùm em voi
Tự luận
Câu 1 :
Trích mẫu thử
Cho $Ba(HCO_3)_2$ vào mẫu thử
- mẫu thử tạo khí không màu là $HCl$
$Ba(HCO_3)_2 + 2HCl \to BaCl_2 + 2CO_2 + 2H_2O$
- MT tạo kết tủa trắng là $Na_2SO_4$
$Ba(HCO_3)_2 + Na_2SO_4 \to BaSO_4 + 2NaHCO_3$
- MT tạo khí không màu và kết tủa trắng là $H_2SO_4$
$Ba(HCO_3)_2 + H_2SO_4 \to BaSO_4 + 2CO_2 + 2H_2O$
- MT không hiện tượng là $NaCl$
Câu 2 :
$S + O_2 \xrightarrow{t^o} SO_2$
$2SO_2 + O_2 \xrightarrow{t^o} 2SO_3$
$SO_3 + H_2O \to H_2SO_4$
$NaCl + H_2SO_{4_{đặc}} \xrightarrow{t^o} NaHSO_4 + HCl$
Câu 3 :
a) $2Al + 6HCl \to 2AlCl_3 + 3H_2$
$n_{HCl} = 0,1.3 = 0,3(mol)$
$n_{Al} = \dfrac{1}{3}n_{HCl} = 0,1(mol)$
$n_{H_2} = \dfrac{1}{2}n_{HCl} = 0,15(mol)$
Suy ra:
$m = 0,1.27 = 2,7(gam)$
$V = 0,15.22,4 = 3,36(lít)$
Đúng 3
Bình luận (0)
Trắc nghiệm:
Câu 1: C
Câu 2: A
Câu 3: D
Câu 4: D
Câu 5: D
Câu 6: B
Câu 7: C
Câu 8: B
Đúng 2
Bình luận (0)
Trắc nghiệm
1.C 2.A 3.D 4.D 5.D 6.B và D 7.C 8B
Đúng 2
Bình luận (0)
Chứng minh rằng: 9^7+81^4 - 27^5 chia hết cho 7
Giải nhanh dùm mik nha!!!
Bài làm :
Ta có :
\(9^7+81^4-27^5\)
\(=\left(3^2\right)^7+\left(3^4\right)^4-\left(3^3\right)^5\)
\(=3^{14}+3^{16}-3^{15}\)
\(=3^{14}\left(1+3^2-3\right)\)
\(=3^{14}.7⋮7\)
=> Điều phải chứng minh
giải dùm em mấy câu này vs ạ nãy em ghi còn thiếu
em cảm ơn mn nhiều giải thích rọ dùm em luôn vs ạ


3.
Từ BBT ta thấy hàm đồng biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(1;+\infty\right)\)
B đúng
4.
Từ BBT ta thấy hàm đồng biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(0;1\right)\)
A đúng
1.
B sai (thiếu điều kiện \(f'\left(x\right)=0\) tại hữu hạn điểm)
Đúng 3
Bình luận (1)
Câu 2 đề thiếu yêu cầu
Câu 9:
Từ đồ thị ta thấy hàm đồng biến trên các khoảng \(\left(-\infty;0\right)\) và \(\left(2;+\infty\right)\)
\(\Rightarrow\) A đúng do \(\left(-1;0\right)\subset\left(-\infty;0\right)\)
Đúng 2
Bình luận (0)
mọi người giải dùm em vs ạ bạn em nhờ em hỏi dùm
em cảm ơn nhiều
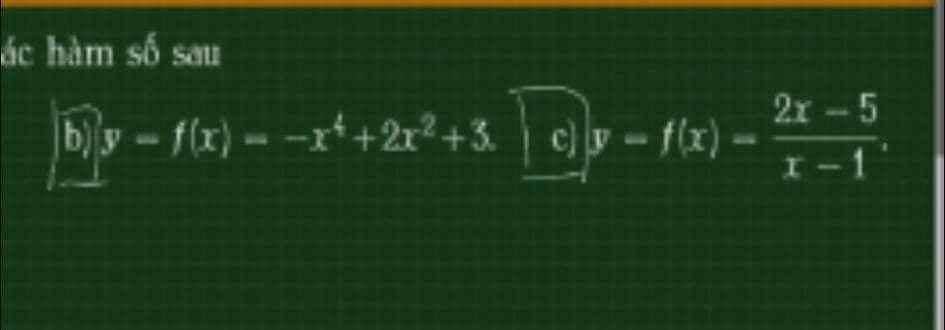

cái hồi nãy thiếu câu hỏi em bổ sung ở dưới này ạ
em cảm ơn mn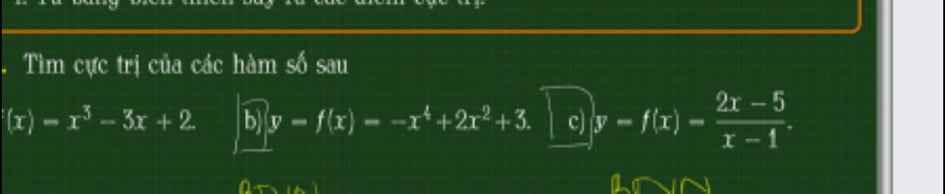
Đúng 0
Bình luận (1)
5.
TXĐ: \(D=\left(-\infty;-1\right)\cup\left(-1;+\infty\right)\)
\(y'=\dfrac{2}{\left(x+1\right)^2}>0\) ; \(\forall x\in D\)
\(\Rightarrow\) Hàm đồng biến trên mỗi khoảng xác định
Hay hàm đồng biến trên \(\left(-\infty;-1\right)\) và \(\left(-1;+\infty\right)\)
6.
\(y=4x^3-4x=0\Rightarrow\left[{}\begin{matrix}x=0\\x=-1\\x=1\end{matrix}\right.\)
Dấu của y' trên trục số:
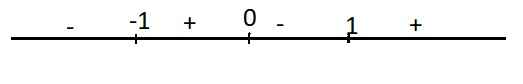
Từ đó ta thấy:
Hàm đồng biến trên các khoảng \(\left(-1;0\right)\) và \(\left(1;+\infty\right)\)
Hàm nghịch biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(1;+\infty\right)\)
Đúng 0
Bình luận (0)
Tìm cực trị
a.
\(f'\left(x\right)=3x^2-3=0\Rightarrow x=\pm1\)
\(f''\left(x\right)=6x\)
\(f''\left(-1\right)=-6< 0\)
\(f''\left(1\right)=6>0\)
\(\Rightarrow x=-1\) là điểm cực đại và \(x=1\) là điểm cực tiểu
b.
\(f'\left(x\right)=-4x^3+4x=0\Rightarrow\left[{}\begin{matrix}x=0\\x=-1\\x=1\end{matrix}\right.\)
\(f''\left(x\right)=-12x^2+4\)
\(f''\left(0\right)=4>0\) ; \(f''\left(-1\right)=-8< 0\) ; \(f''\left(1\right)=-8< 0\)
\(\Rightarrow x=0\) là điểm cực tiểu và \(x=\pm1\) là 2 điểm cực đại
c.
\(f'\left(x\right)=\dfrac{3}{\left(x-1\right)^2}\ne0\) với mọi x thuộc miền xác định
Hàm không có cực trị
Đúng 0
Bình luận (0)

















